R finetune tune_race_anova 通过方差分析模型进行高效网格搜索

tune_race_anova() 为一组预定义的调整参数计算一组性能指标(例如，准确性或 RMSE)，这些参数对应于一次或多次数据重采样的模型或配方。在评估初始数量的重采样后，该过程消除了使用重复测量方差分析模型不太可能获得最佳结果的调整参数组合。

用法

tune_race_anova(object, ...)

# S3 method for model_spec
tune_race_anova(
  object,
  preprocessor,
  resamples,
  ...,
  param_info = NULL,
  grid = 10,
  metrics = NULL,
  control = control_race()
)

# S3 method for workflow
tune_race_anova(
  object,
  resamples,
  ...,
  param_info = NULL,
  grid = 10,
  metrics = NULL,
  control = control_race()
)

参数

object: parsnip 模型规范或 workflows::workflow() 。
...: 目前未使用。
preprocessor: 使用 recipes::recipe() 创建的传统模型公式或配方。仅当 object 不是工作流程时才需要这样做。
resamples: 具有多次重采样的 rset() 对象(即不是验证集)。
param_info: dials::parameters() 对象或 NULL 。如果没有给出，则从其他参数派生参数集。当需要自定义参数范围时，传递此参数可能很有用。
grid: 调谐组合或正整数的 DataFrame 。 DataFrame 应具有用于调整每个参数的列和用于调整候选参数的行。整数表示要自动创建的候选参数集的数量。
metrics: 一个 yardstick::metric_set() 或 NULL 。
control: 用于修改调整过程的对象。有关更多详细信息，请参阅control_race()。

值

具有主类 tune_race 的对象，其标准格式与 tune::tune_grid() 生成的对象相同。

细节

Kuhn (2014) 说明了该方法的技术细节。

竞赛方法是网格搜索的有效方法。最初，该函数评估一小组初始重采样的所有调整参数。 control_race() 的 burn_in 参数设置初始重新采样的数量。

对这些重新采样的性能统计数据进行分析，以确定哪些调整参数在统计上与当前最佳设置没有差异。如果参数在统计上不同，则将其排除在进一步重采样之外。

下一次重新采样将与剩余的参数组合一起使用，并更新统计分析。处理每个新的重采样时可以排除更多候选参数。

该函数使用重复测量方差分析模型确定统计显著性，其中性能统计数据(例如 RMSE、准确性等)是结果数据，随机效应是由于重新采样造成的。 control_race() 函数包含应用于方差分析结果的显著性截止参数以及其他相关参数。

将竞赛方法与并行处理结合使用是有好处的。下一节显示了一个数据集和模型的结果基准。

基准测试结果

为了进行演示，我们使用带有 kernlab 包的 SVM 模型。

library(kernlab)
library(tidymodels)
library(finetune)
library(doParallel)

## -----------------------------------------------------------------------------

data(cells, package = "modeldata")
cells <- cells %>% select(-case)

## -----------------------------------------------------------------------------

set.seed(6376)
rs <- bootstraps(cells, times = 25)

我们只会调整模型参数(即不调整配方)：

## -----------------------------------------------------------------------------

svm_spec <-
  svm_rbf(cost = tune(), rbf_sigma = tune()) %>%
  set_engine("kernlab") %>%
  set_mode("classification")

svm_rec <-
  recipe(class ~ ., data = cells) %>%
  step_YeoJohnson(all_predictors()) %>%
  step_normalize(all_predictors())

svm_wflow <-
  workflow() %>%
  add_model(svm_spec) %>%
  add_recipe(svm_rec)

set.seed(1)
svm_grid <-
  svm_spec %>%
  parameters() %>%
  grid_latin_hypercube(size = 25)

我们将获得有和没有并行处理的网格搜索和方差分析竞赛的时间：

## -----------------------------------------------------------------------------
## Regular grid search

system.time({
  set.seed(2)
  svm_wflow %>% tune_grid(resamples = rs, grid = svm_grid)
})

##    user  system elapsed 
## 741.660  19.654 761.357

## -----------------------------------------------------------------------------
## With racing

system.time({
  set.seed(2)
  svm_wflow %>% tune_race_anova(resamples = rs, grid = svm_grid)
})

##    user  system elapsed 
## 133.143   3.675 136.822

赛车加速 5.56 倍。

## -----------------------------------------------------------------------------
## Parallel processing setup

cores <- parallel::detectCores(logical = FALSE)
cores

## [1] 10

cl <- makePSOCKcluster(cores)
registerDoParallel(cl)

## -----------------------------------------------------------------------------
## Parallel grid search

system.time({
  set.seed(2)
  svm_wflow %>% tune_grid(resamples = rs, grid = svm_grid)
})

##  user  system elapsed 
## 1.112   0.190 126.650

网格搜索并行处理比顺序网格搜索快 6.01 倍。

## -----------------------------------------------------------------------------
## Parallel racing

system.time({
  set.seed(2)
  svm_wflow %>% tune_race_anova(resamples = rs, grid = svm_grid)
})

##  user  system elapsed 
## 1.908   0.261  21.442

与赛车并行处理比顺序网格搜索快 35.51 倍。

竞速和并行处理会产生复合效应，但其大小取决于模型类型、重采样次数、调整参数数量等。

参考

Kuhn, M 2014。“机器学习模型交叉验证中的无效性分析”。 https://arxiv.org/abs/1405.6974。

也可以看看

tune::tune_grid() , control_race() , tune_race_win_loss()

例子

# \donttest{
library(parsnip)
library(rsample)
library(dials)
#> Loading required package: scales

## -----------------------------------------------------------------------------

if (rlang::is_installed(c("discrim", "lme4", "modeldata"))) {
  library(discrim)
  data(two_class_dat, package = "modeldata")

  set.seed(6376)
  rs <- bootstraps(two_class_dat, times = 10)

  ## -----------------------------------------------------------------------------

  # optimize an regularized discriminant analysis model
  rda_spec <-
    discrim_regularized(frac_common_cov = tune(), frac_identity = tune()) %>%
    set_engine("klaR")

  ## -----------------------------------------------------------------------------

  ctrl <- control_race(verbose_elim = TRUE)
  set.seed(11)
  grid_anova <-
    rda_spec %>%
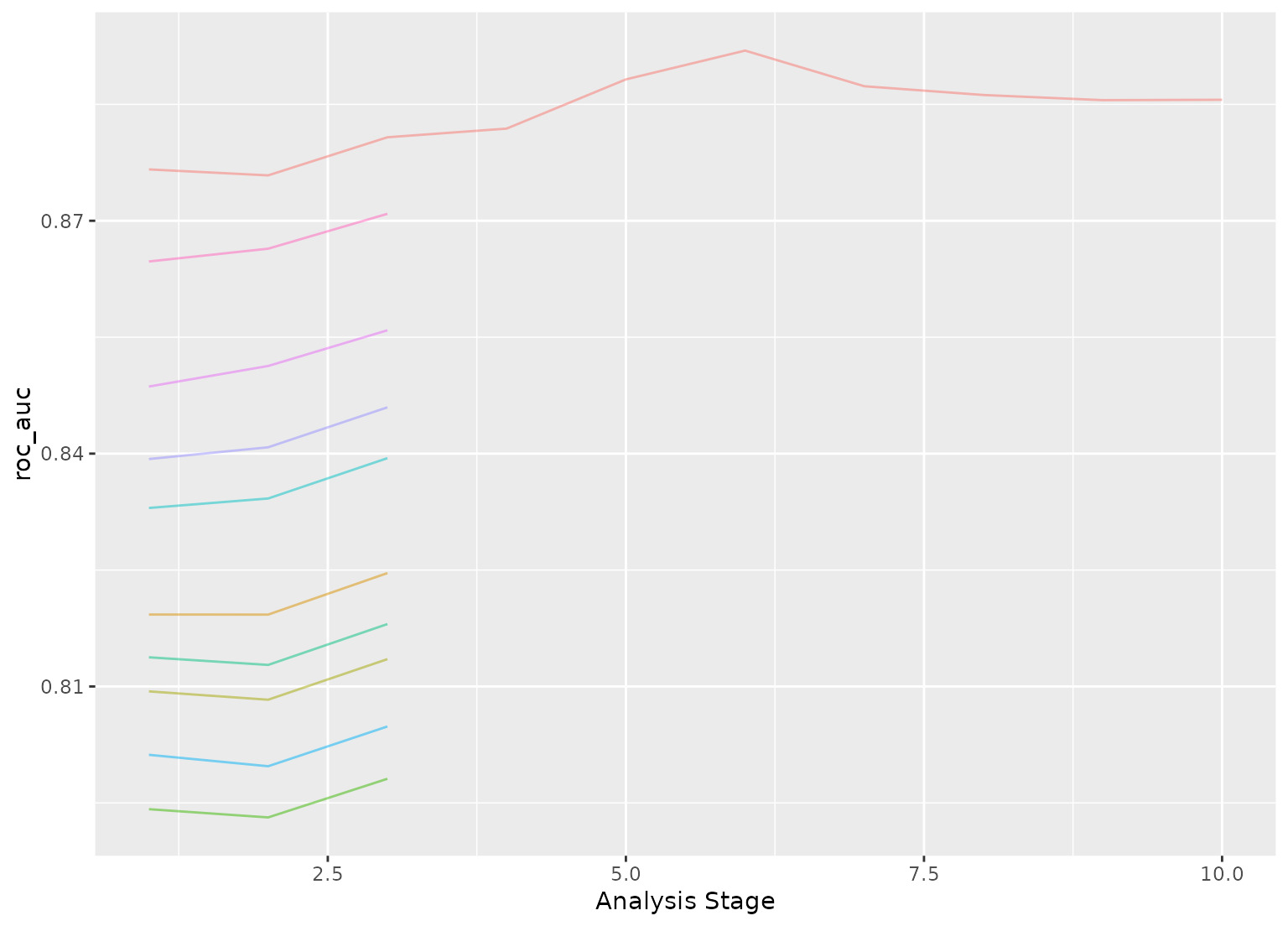
    tune_race_anova(Class ~ ., resamples = rs, grid = 10, control = ctrl)

  # Shows only the fully resampled parameters
  show_best(grid_anova, metric = "roc_auc", n = 2)

  plot_race(grid_anova)
}
#> 
#> Attaching package: ‘discrim’
#> The following object is masked from ‘package:dials’:
#> 
#>     smoothness
#> ℹ Racing will maximize the roc_auc metric.
#> ℹ Resamples are analyzed in a random order.
#> ℹ Bootstrap05: All but one parameter combination were eliminated.

# }

源代码：R/tune_race_anova.R

相关用法

注：本文由纯净天空筛选整理自Max Kuhn等大神的英文原创作品 Efficient grid search via racing with ANOVA models。非经特殊声明，原始代码版权归原作者所有，本译文未经允许或授权，请勿转载或复制。