Python SciPy qmc.PoissonDisk用法及代码示例

本文简要介绍 python 语言中 scipy.stats.qmc.PoissonDisk 的用法。

用法:

class  scipy.stats.qmc.PoissonDisk(d, *, radius=0.05, hypersphere='volume', ncandidates=30, optimization=None, seed=None)#

泊松盘采样。

参数 ：：

d： int

参数空间的维度。

radius： 浮点数

对新候选者进行采样时点之间保持的最小距离。

hypersphere： {“volume”, “surface”}，可选

用于生成要添加到最终样本中的潜在候选者的抽样策略。默认为“volume”。

• volume：原始 Bridson 算法，如中所述[1]。对新候选人进行抽样之内超球面。

• surface ：仅对超球面的表面进行采样。

ncandidates： int

每次迭代采样的候选数。更多候选者会导致更密集的采样，因为每次迭代可以接受更多候选者。

optimization： {无，“random-cd”，“lloyd”}，可选

是否使用优化方案来提高采样后的质量。请注意，这是一个后处理步骤，不能保证样品的所有属性都得到保留。默认为“无”。

• random-cd：坐标的随机排列以降低中心差异。基于中心差异的最佳样本不断更新。与使用其他差异度量相比，基于中心差异的采样对 2D 和 3D 子投影显示出更好的 space-filling 鲁棒性。

• lloyd：使用修改后的Lloyd-Max 算法扰动样本。该过程收敛到等间隔的样本。

seed： {无，整数， numpy.random.Generator }，可选

如果种子是 int 或 None，一个新的numpy.random.Generator是使用创建的np.random.default_rng(seed).如果种子已经是一个Generator实例，然后使用提供的实例。

注意：

泊松盘采样是一种迭代采样策略。从种子样本开始，在种子周围的超球面中对候选者进行采样。低于一定半径或域外的候选人将被拒绝。新样本被添加到样本种子池中。当池为空或达到所需样本数量时，该过程停止。

样本可以包含的最大点数直接与半径。随着空间维度的增加，更高的半径可以使点分布得更远，有助于克服维数灾难。请参阅准蒙特卡罗教程更多细节。

警告

由于其迭代性质和内存要求，该算法更适合低维度和采样大小。选择高维度的小半径意味着该空间比使用较低维度或较大半径可以包含更多样本。

部分代码取自 [2]，原作者 Shamis 于 2021 年 3 月 31 日书面同意，可在 3 条款 BSD 下的 SciPy 中免费使用。

参考：

[1]

Robert Bridson，“任意维度的快速泊松盘采样”。西格图，2007 年。

[2]

StackOverflow 。

例子：

使用半径 0.2 生成 2D 样本。

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from matplotlib.collections import PatchCollection
>>> from scipy.stats import qmc
>>>
>>> rng = np.random.default_rng()
>>> radius = 0.2
>>> engine = qmc.PoissonDisk(d=2, radius=radius, seed=rng)
>>> sample = engine.random(20)

可视化 2D 样本并显示没有点比半径.radius/2用于可视化不相交的圆。如果两个样本正好位于半径彼此距离，然后是它们的半径圆radius/2会触摸。

>>> fig, ax = plt.subplots()
>>> _ = ax.scatter(sample[:, 0], sample[:, 1])
>>> circles = [plt.Circle((xi, yi), radius=radius/2, fill=False)
...            for xi, yi in sample]
>>> collection = PatchCollection(circles, match_original=True)
>>> ax.add_collection(collection)
>>> _ = ax.set(aspect='equal', xlabel=r'$x_1$', ylabel=r'$x_2$',
...            xlim=[0, 1], ylim=[0, 1])
>>> plt.show()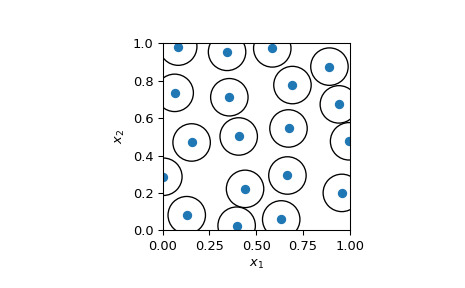

这种可视化可以看作是圆形包装：我们可以在空间中放置多少个圆形。这是一个np-hard问题。方法 fill_space 可用于添加样本，直到无法添加更多样本为止。这是一个难题，可能需要手动调整参数。注意维度：随着维度的增加，填充空间所需的样本数量呈指数增长(curse-of-dimensionality)。