本文簡要介紹 python 語言中 scipy.fft.fht 的用法。
用法:
scipy.fft.fht(a, dln, mu, offset=0.0, bias=0.0)#計算快速漢克爾變換。
使用 FFTLog 算法 [1]、[2] 計算對數間隔周期序列的離散漢克爾變換。
- a: 類似數組 (…, n)
實周期輸入數組,均勻對數間隔。對於多維輸入,變換是在最後一個軸上執行的。
- dln: 浮點數
輸入數組的均勻對數間距。
- mu: 浮點數
漢克爾變換的階數,任何正實數或負實數。
- offset: 浮點數,可選
輸出陣列的均勻對數間距的偏移。
- bias: 浮點數,可選
冪律偏差的指數,任何正或負實數。
- A: 類似數組 (…, n)
變換後的輸出數組是實數、周期性、均勻對數間隔且與輸入數組形狀相同的數組。
參數 ::
返回 ::
注意:
該函數計算漢克爾變換的離散版本
其中 是階數 的貝塞爾函數。索引可以是任何實數,正數或負數。
輸入數組a是一個長度為周期的序列,均勻對數間隔間距丁,
以點為中心。注意中心索引是half-integral如果是偶數,所以位於兩個輸入元素之間。類似地,輸出數組A是一個長度為周期的序列,也均勻地以對數間隔丁
以點 為中心。
中心點和周期間隔的數量可以任意選擇,但通常選擇乘積要團結。可以使用以下命令更改此設置抵消參數,控製對數偏移輸出數組的。選擇一個最佳值抵消可以減少離散漢克爾變換的振鈴。
如果偏置參數非零,則該函數計算偏置漢克爾變換的離散版本
其中的值是偏見,以及冪律偏差應用於輸入序列。偏置變換可以幫助近似連續變換如果有一個值這樣接近於周期序列,在這種情況下得到的結果將接近連續變換。
參考:
[1]塔爾曼 J.D.,1978,J.Comp。物理, 29, 35
[2] (1,2)漢密爾頓 A.J.S.,2000,MNRAS,312, 257 (astro-ph/9905191)
例子:
該示例是[2]中提供的
fftlogtest.f的改編版本。它評估積分>>> import numpy as np >>> from scipy import fft >>> import matplotlib.pyplot as plt變換的參數。
>>> mu = 0.0 # Order mu of Bessel function >>> r = np.logspace(-7, 1, 128) # Input evaluation points >>> dln = np.log(r[1]/r[0]) # Step size >>> offset = fft.fhtoffset(dln, initial=-6*np.log(10), mu=mu) >>> k = np.exp(offset)/r[::-1] # Output evaluation points定義分析函數。
>>> def f(x, mu): ... """Analytical function: x^(mu+1) exp(-x^2/2).""" ... return x**(mu + 1)*np.exp(-x**2/2)評估
r處的函數並使用 FFTLog 計算k處的相應值。>>> a_r = f(r, mu) >>> fht = fft.fht(a_r, dln, mu=mu, offset=offset)對於此示例,我們實際上可以計算分析響應(在本例中與輸入函數相同)進行比較並計算相對誤差。
>>> a_k = f(k, mu) >>> rel_err = abs((fht-a_k)/a_k)繪製結果。
>>> figargs = {'sharex': True, 'sharey': True, 'constrained_layout': True} >>> fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 4), **figargs) >>> ax1.set_title(r'$r^{\mu+1}\ \exp(-r^2/2)$') >>> ax1.loglog(r, a_r, 'k', lw=2) >>> ax1.set_xlabel('r') >>> ax2.set_title(r'$k^{\mu+1} \exp(-k^2/2)$') >>> ax2.loglog(k, a_k, 'k', lw=2, label='Analytical') >>> ax2.loglog(k, fht, 'C3--', lw=2, label='FFTLog') >>> ax2.set_xlabel('k') >>> ax2.legend(loc=3, framealpha=1) >>> ax2.set_ylim([1e-10, 1e1]) >>> ax2b = ax2.twinx() >>> ax2b.loglog(k, rel_err, 'C0', label='Rel. Error (-)') >>> ax2b.set_ylabel('Rel. Error (-)', color='C0') >>> ax2b.tick_params(axis='y', labelcolor='C0') >>> ax2b.legend(loc=4, framealpha=1) >>> ax2b.set_ylim([1e-9, 1e-3]) >>> plt.show()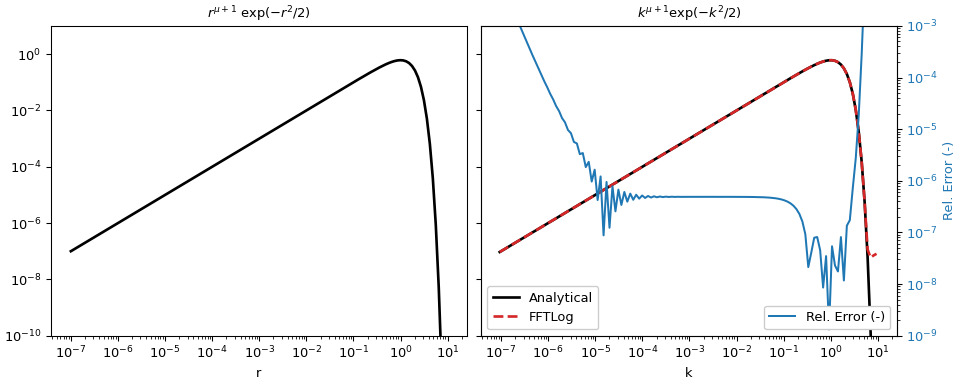
相關用法
- Python SciPy fft.fhtoffset用法及代碼示例
- Python SciPy fft.fft2用法及代碼示例
- Python SciPy fft.fftn用法及代碼示例
- Python SciPy fft.fftfreq用法及代碼示例
- Python SciPy fft.fft用法及代碼示例
- Python SciPy fft.fftshift用法及代碼示例
- Python SciPy fft.idctn用法及代碼示例
- Python SciPy fft.next_fast_len用法及代碼示例
- Python SciPy fft.ifft2用法及代碼示例
- Python SciPy fft.ifftn用法及代碼示例
- Python SciPy fft.ihfftn用法及代碼示例
- Python SciPy fft.rfftfreq用法及代碼示例
- Python SciPy fft.dctn用法及代碼示例
- Python SciPy fft.rfft用法及代碼示例
- Python SciPy fft.dct用法及代碼示例
- Python SciPy fft.idstn用法及代碼示例
- Python SciPy fft.rfftn用法及代碼示例
- Python SciPy fft.hfft用法及代碼示例
- Python SciPy fft.set_global_backend用法及代碼示例
- Python SciPy fft.ifftshift用法及代碼示例
- Python SciPy fft.ihfft用法及代碼示例
- Python SciPy fft.irfftn用法及代碼示例
- Python SciPy fft.set_backend用法及代碼示例
- Python SciPy fft.idct用法及代碼示例
- Python SciPy fft.get_workers用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.fft.fht。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
