本文簡要介紹 python 語言中 scipy.fft.fft 的用法。
用法:
scipy.fft.fft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None, *, plan=None)#計算一維離散傅裏葉變換。
該函數計算一維n具有高效快速傅裏葉變換 (FFT) 算法的點離散傅裏葉變換 (DFT)[1].
- x: array_like
輸入數組,可以很複雜。
- n: 整數,可選
輸出的變換軸的長度。如果 n 小於輸入的長度,則裁剪輸入。如果它更大,則用零填充輸入。如果未給出 n,則使用沿軸指定的軸的輸入長度。
- axis: 整數,可選
計算 FFT 的軸。如果未給出,則使用最後一個軸。
- norm: {“backward”, “ortho”, “forward”},可選
標準化模式。默認值為“backward”,這意味著在
ifft上的正向變換和縮放1/n沒有標準化。 “forward” 改為在正向變換上應用1/n因子。對於norm="ortho",兩個方向都按1/sqrt(n)縮放。- overwrite_x: 布爾型,可選
如果為 True,則 x 的內容可以被銷毀;默認為假。有關詳細信息,請參閱下麵的注釋。
- workers: 整數,可選
用於並行計算的最大工作線程數。如果為負,則該值從
os.cpu_count()環繞。請參閱下麵的更多細節。- plan: 對象,可選
此參數保留用於傳遞下遊 FFT 供應商提供的預先計算的計劃。它目前未在 SciPy 中使用。
- out: 複雜的ndarray
截斷或補零的輸入,沿軸指示的軸轉換,如果未指定軸,則為最後一個。
- IndexError
如果軸大於 x 的最後一個軸。
參數 ::
返回 ::
拋出 ::
注意:
FFT(快速傅裏葉變換)是指通過在計算項中使用對稱性,可以有效計算離散傅裏葉變換 (DFT) 的一種方式。對稱性最高的時候n是 2 的冪,因此對於這些大小,變換是最有效的。對於難以分解的大小,
scipy.fft使用 Bluestein 算法[2]所以永遠不會比 O(n日誌n)。通過使用零填充輸入可以看到進一步的性能改進scipy.fft.next_fast_len.如果
x是一維數組,則fft相當於y[k] = np.sum(x * np.exp(-2j * np.pi * k * np.arange(n)/n))頻率項
f=k/n位於y[k]。在y[n/2],我們達到了奈奎斯特頻率並環繞到負頻率項。因此,對於 8 點變換,結果的頻率為 [0, 1, 2, 3, -4, -3, -2, -1]。要重新排列 fft 輸出以使 zero-frequency 組件居中,例如 [-4, -3, -2, -1, 0, 1, 2, 3],請使用fftshift。可以以單精度、雙精度或擴展精度(長雙精度)浮點數進行轉換。半精度輸入將轉換為單精度,非浮點輸入將轉換為雙精度。
如果
x的數據類型為實數,則自動使用“real FFT”算法,計算時間大致減半。為了進一步提高效率,請使用rfft,它執行相同的計算,但隻輸出對稱頻譜的一半。如果數據既真實又對稱,dct可以通過從一半信號生成一半頻譜,再次使效率翻倍。當指定
overwrite_x=True時,x引用的內存可以由實現以任何方式使用。這可能包括為結果重用內存,但這絕不是保證。您不應該在轉換後依賴x的內容,因為這可能會在未來發生變化而不會發出警告。workers參數指定將 FFT 計算拆分成的最大並行作業數。這將在x內執行獨立的一維 FFT。因此,x必須至少是二維的,並且未轉換的軸必須足夠大以拆分成塊。如果x太小,使用的作業可能比請求的少。參考:
[1]Cooley、James W. 和 John W. Tukey,1965 年,“複雜傅裏葉級數的機器計算算法”,數學。計算。 19:297-301。
[2]Bluestein, L.,1970,“計算離散傅裏葉變換的線性濾波方法”。 IEEE 音頻和電聲學匯刊。 18 (4): 451-455。
例子:
>>> import scipy.fft >>> import numpy as np >>> scipy.fft.fft(np.exp(2j * np.pi * np.arange(8) / 8)) array([-2.33486982e-16+1.14423775e-17j, 8.00000000e+00-1.25557246e-15j, 2.33486982e-16+2.33486982e-16j, 0.00000000e+00+1.22464680e-16j, -1.14423775e-17+2.33486982e-16j, 0.00000000e+00+5.20784380e-16j, 1.14423775e-17+1.14423775e-17j, 0.00000000e+00+1.22464680e-16j])在此示例中,實數輸入具有 Hermitian 的 FFT,即實部對稱而虛部反對稱:
>>> from scipy.fft import fft, fftfreq, fftshift >>> import matplotlib.pyplot as plt >>> t = np.arange(256) >>> sp = fftshift(fft(np.sin(t))) >>> freq = fftshift(fftfreq(t.shape[-1])) >>> plt.plot(freq, sp.real, freq, sp.imag) [<matplotlib.lines.Line2D object at 0x...>, <matplotlib.lines.Line2D object at 0x...>] >>> plt.show()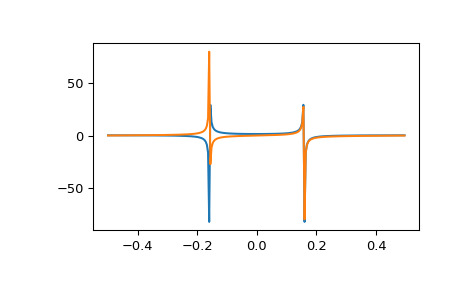
相關用法
- Python SciPy fft.fft2用法及代碼示例
- Python SciPy fft.fftn用法及代碼示例
- Python SciPy fft.fftfreq用法及代碼示例
- Python SciPy fft.fftshift用法及代碼示例
- Python SciPy fft.fht用法及代碼示例
- Python SciPy fft.fhtoffset用法及代碼示例
- Python SciPy fft.idctn用法及代碼示例
- Python SciPy fft.next_fast_len用法及代碼示例
- Python SciPy fft.ifft2用法及代碼示例
- Python SciPy fft.ifftn用法及代碼示例
- Python SciPy fft.ihfftn用法及代碼示例
- Python SciPy fft.rfftfreq用法及代碼示例
- Python SciPy fft.dctn用法及代碼示例
- Python SciPy fft.rfft用法及代碼示例
- Python SciPy fft.dct用法及代碼示例
- Python SciPy fft.idstn用法及代碼示例
- Python SciPy fft.rfftn用法及代碼示例
- Python SciPy fft.hfft用法及代碼示例
- Python SciPy fft.set_global_backend用法及代碼示例
- Python SciPy fft.ifftshift用法及代碼示例
- Python SciPy fft.ihfft用法及代碼示例
- Python SciPy fft.irfftn用法及代碼示例
- Python SciPy fft.set_backend用法及代碼示例
- Python SciPy fft.idct用法及代碼示例
- Python SciPy fft.get_workers用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.fft.fft。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
