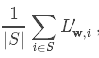下麵是章節優化的目錄(參見全文目錄)
數學描述
梯度下降
解決這類函數 minw∈Rdf(w) 優化問題的最簡單方法是 梯度下降(gradient descent)。這樣的一階優化方法(包括梯度下降和隨機梯度下降)非常適合大規模分布式計算。
梯度下降法旨在下降最快的方向進行迭代從而找到局部最小值。這個最快的方向是函數當前點的負導數(也叫梯度)。如果目標函數f對所有參數不可導,但具有凸函數性質,那麽可以使用次梯度(次梯度是梯度的一種自然泛化)來扮演下降方向的角色。不管哪種情況,計算函數f的梯度或者次梯度開銷都比較大——因為需要遍曆整個數據集,從而計算所有損失項的貢獻。
隨機梯度下降 (SGD)
求和形式的目標函數f的優化問題特別適合使用隨機梯度下降法(SGD)求解。通常在有監督機器學習中使用的優化公式:
 這個公式看起來很自然,因為損失的計算方式是請求每個獨立數據點損失的平均值。
這個公式看起來很自然,因為損失的計算方式是請求每個獨立數據點損失的平均值。
隨機次梯度是在向量上做一個隨機選擇,從而在期望上來看,我們獲得了原始目標函數的真正次梯度。具體方法是:一致性隨機抽樣一個數據點i∈[1..n] ,我們可以通過下麵式子獲得目標函數(1)中的次梯度:
 其中
其中 L′w,i∈Rd是在第i個點處,損失函數的次梯度,也就是說,
![]() 並且,
並且,R′w 不依賴於隨機選擇的樣本點。顯然,在隨機選擇的點i∈[1..n]上,我們獲得了f′w,i,它是原始目標函數f的次梯度,亦即:
![]() 有了梯度公式之後,SGD就可以簡單地按負隨機次梯度
有了梯度公式之後,SGD就可以簡單地按負隨機次梯度f′w,i的方向前進就可以了,即:
Step-size(步長). 參數γ就是步長(Step-size)。在默認實現中,步長迭代次數平方根的增大而減小:γ = s / sqrt(t),其中s是輸入參數stepSize,t是表示的是第t次迭代。注意SGD最好步長的選擇實際上比較微妙,是個熱門研究課題。
Gradients(梯度). MLlib中實現的機器學習方法的梯度列表可以在章節分類和回歸[Classification and regression]看到。
Proximal Updates(近似更新). 作為在前進方向上使用正則化梯度 R′(w) 的另一種選擇,一種通過使用近似操作的改進更新方法可以應用於某些場景。對於L1正則化,近似操作是軟閾值法(soft thresholding)[signum(w) * max(0.0, abs(w) – shrinkageVal) ],這個在 L1Updater中實現,這種方法可以是產生的w具有更好的稀疏性。
分布式SGD的更新機製
GradientDescent中實現的SGD對樣本數據使用了一種簡單的分布式抽樣。回想一下公式(1)的優化問題,其中的損失函數部分為:
miniBatchFraction來指定使用部分數據替代使用全部數據。在這個子集上的平均梯度如下:在每一輪迭代中,RDD上的抽樣以及對每個worker機器部分結果的求和計算都由標磚spark程序完成。
如果將miniBatchFraction置為1,那麽每一輪迭代中都使用準確梯度下降。這種情況下,在前進方向上就沒有了隨機性和差異。另外一種極端情況下,如果minBatchFraction設置得太小,比如隻有一個點被抽樣出來,也就是|S|= miniBatchFraction×n=1,那麽算法就變成了標準的SGD。這種情況下,前進方向取決於數據點的一致性隨機抽樣。
有限內存BFGS (L-BFGS)
L-BFGS 是擬牛頓法家族的一員,用來解決函數 minw∈Rdf(w) 的優化問題。L-BFGS算法對目標函數做局部近似,它不需要求目標函數第二部分的導數來構造Hession矩陣。Hessian矩陣通過上一步的梯度來估值,因而使用牛頓法計算Hession矩陣沒有垂直擴展問題(訓練特征的數量)。所以,L-BFGS比其他一階優化方法收斂更快。
補充:
牛頓法收斂速度快,但是計算過程中需要計算目標函數的二階偏導數,難度較大;目標函數的Hessian矩陣無法保持正定,從而令牛頓法失效。
為了解決這兩個問題,人們提出了擬牛頓法,即“模擬”牛頓法的改進型算法。基本思想是不用二階偏導數而構造出可以近似Hessian矩陣的逆的正定對稱陣,從而在“擬牛頓”的條件下優化目標函數。Hessian陣的構造方法的不同決定了不同的擬牛頓法。
選擇優化方法
線性方法 會在內部使用優化算法,MLlib中的部分線性方法支持SGD和L-BFGS。不同的優化方法會有不同的收斂速度保障,這依賴於目標函數的特點,這裏不討論這個問題。通常,如果L-BFGS是可用的,為了更快的收斂(更少的迭代),建議使用L-BFGS而不是SGD。
MLlib中的實現
梯度下降和隨機梯度下降
梯度下降包括隨機梯度下降(SGD)作為MLlib中的底層原語,各種ML算法都會用到,可以參考:線性方法 章節中的例子。
SGD類GradientDescent 有下列參數:
Gradient 計算待優化函數隨機梯度的類。也就是給定單個訓練樣本以及當前的參數值,計算隨機梯度。MLlib包含了常用損失函數的梯度類,這些損失函數可以是:hinge, logistic, least-squares等。梯度類的輸入是訓練樣本,樣本標記以及當前的參數。Updater實際執行梯度下降步驟的類。也就是給定損失部分的梯度,在每輪迭代中更新權值。Updater也負責正則化部分的更新。MLlib中的更新可以支持:不做正則化,L1正則化,L2正則化。stepSize梯度下降的初始步長。Updater在第t步使用的步長是stepSize/sqrt(t)。numIterations迭代次數。regParam使用L1或L2時的正則化參數。miniBatchFraction 每輪迭代中抽取的用於梯度計算的數據比例。- 抽樣也需要遍曆整個RDD,所以減小miniBatchFraction不一定會大幅提升優化速度。如果梯度計算開銷很大時,使用抽樣的方法計算梯度會有可觀的性能提升。
L-BFGS
L-BFGS當前隻是MLlib中的底層優化原語。如果需要在不同的機器學習算法(例如線性回歸、邏輯回歸)使用L-BFGS,需要自己傳入目標函數的梯度以及Updater,這個跟直接使用LogisticRegressionWithSGD的API不一樣。下一個版本會發布L-BFGS比較完備的優化功能。
L1Updater使用的L1正則化當前在L-BFGS中不可用,因為L1Updater中的軟閾值(soft-thresholding)是為梯度下降設計的。參見開發者注意事項。
L-BFGS方法LBFGS.runLBFGS有下列參數:
Gradient計算待優化函數隨機梯度的類。也就是給定單個訓練樣本以及當前的參數值,計算隨機梯度。MLlib包含了常用損失函數的梯度類,這些損失函數可以是:hinge, logistic, least-squares等。梯度類的輸入是訓練樣本,樣本標記以及當前的參數。Updater為L-BFGS計算損失函數和正則化梯度的類。目前支持無正則化和L2正則化。numCorrections用在L-BFGS更新中的修正次數。推薦10。maxNumIterations 最大迭代次數。regParam正則化參數。convergenceTol收斂閾值。這個值必須是非負的。值越小越嚴格,通常會導致更多的迭代次數。在Breeze LBFGS中這個值涉及到平均提升和梯度範數。
該函數的返回值是二個元素的元組。第一個元素是包含每個特征權值的列矩陣,第二個元素是包含每次迭代損失的數組。
下麵是用來訓練二分邏輯會就的例子(Scala),使用了L2正則化以及L-BFGS優化器。
import org.apache.spark.SparkContext
import org.apache.spark.mllib.evaluation.BinaryClassificationMetrics
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.util.MLUtils
import org.apache.spark.mllib.classification.LogisticRegressionModel
import org.apache.spark.mllib.optimization.{LBFGS, LogisticGradient, SquaredL2Updater}
val data = MLUtils.loadLibSVMFile(sc, "data/mllib/sample_libsvm_data.txt")
val numFeatures = data.take(1)(0).features.size
// Split data into training (60%) and test (40%).
val splits = data.randomSplit(Array(0.6, 0.4), seed = 11L)
// Append 1 into the training data as intercept.
val training = splits(0).map(x => (x.label, MLUtils.appendBias(x.features))).cache()
val test = splits(1)
// Run training algorithm to build the model
val numCorrections = 10
val convergenceTol = 1e-4
val maxNumIterations = 20
val regParam = 0.1
val initialWeightsWithIntercept = Vectors.dense(new Array[Double](numFeatures + 1))
val (weightsWithIntercept, loss) = LBFGS.runLBFGS(
training,
new LogisticGradient(),
new SquaredL2Updater(),
numCorrections,
convergenceTol,
maxNumIterations,
regParam,
initialWeightsWithIntercept)
val model = new LogisticRegressionModel(
Vectors.dense(weightsWithIntercept.toArray.slice(0, weightsWithIntercept.size - 1)),
weightsWithIntercept(weightsWithIntercept.size - 1))
// Clear the default threshold.
model.clearThreshold()
// Compute raw scores on the test set.
val scoreAndLabels = test.map { point =>
val score = model.predict(point.features)
(score, point.label)
}
// Get evaluation metrics.
val metrics = new BinaryClassificationMetrics(scoreAndLabels)
val auROC = metrics.areaUnderROC()
println("Loss of each step in training process")
loss.foreach(println)
println("Area under ROC = " + auROC)開發者注意事項
因為Hessian矩陣是通過對之前梯度的評估值來近似構建的,所以目標函數在優化過程中不能修改。也就是說,使用miniBatch的隨機L-BFGS不能天然正常工作,因此,在有更好的解決方案之前我們不提供隨機L-BFGS這個功能。
Updater原來隻是是為梯度下降計算設計的類。然而,我們可以將損失函數和正則化的梯度計算用於L-BFGS,不過要忽略掉隻針對梯度將下降部分的邏輯(例如:自適應步長功能)。We will refactorize this into regularizer to replace updater to separate the logic between regularization and step update later.
參考:
[1] http://blog.sina.com.cn/s/blog_5f234d47010162f7.html