scipy.stats.beta()是一个beta连续随机变量,使用标准格式和一些形状参数进行定义以完成其规格。
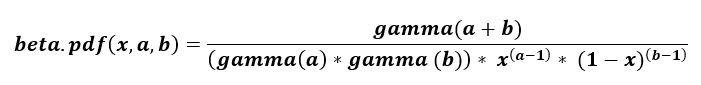
参数:
q :上下尾概率
a,b:形状参数
x :分位数
loc :[可选]位置参数。默认值= 0
scale :[可选]比例参数。默认值= 1
size :[int型元组,可选]形状或随机变量。
moments :[可选]由字母['mvsk']组成; “ m” =均值,“ v” =方差,“ s” = Fisher的偏度,“ k” = Fisher的峰度。 (默认=“ MV”)。
结果:beta连续随机变量
代码1:创建Beta连续随机变量
# importing scipy
from scipy.stats import beta
numargs = beta.numargs
[a, b] = [0.6, ] * numargs
rv = beta(a, b)
print ("RV : \n", rv)输出:
RV : <scipy.stats._distn_infrastructure.rv_frozen object at 0x0000029482FCC438>
代码2:β随机变量和概率分布函数。
import numpy as np
quantile = np.arange (0.01, 1, 0.1)
# Random Variates
R = beta.rvs(a, b, scale = 2, size = 10)
print ("Random Variates : \n", R)
# PDF
R = beta.pdf(quantile, a, b, loc = 0, scale = 1)
print ("\nProbability Distribution : \n", R)输出:
Random Variates : [1.47189604 1.47284574 1.84692416 1.0686604 0.32709236 1.96857076 0.00639731 1.97093898 1.34811881 0.34269426] Probability Distribution : [2.62281037 1.04883674 0.84934164 0.76724957 0.73040985 0.72096547 0.73529768 0.77903762 0.8752367 1.1264383 ]
代码3:图形表示。
import numpy as np
import matplotlib.pyplot as plt
distribution = np.linspace(0, np.maximum(rv.dist.b, 5))
plot = plt.plot(distribution, rv.pdf(distribution))输出:

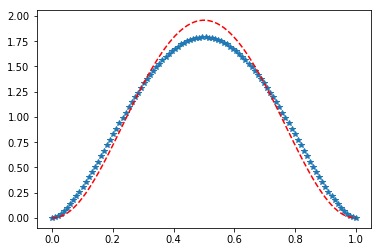
代码4:改变位置参数
from scipy.stats import arcsine
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 1.0, 100)
# Varying positional arguments
y1 = beta.pdf(x, 2.75, 2.75)
y2 = beta.pdf(x, 3.25, 3.25)
plt.plot(x, y1, "*", x, y2, "r--")输出:
相关用法
- Python Scipy stats.chi()用法及代码示例
- Python Scipy stats.f()用法及代码示例
- Python Scipy stats.hmean()用法及代码示例
- Python Scipy stats.halflogistic()用法及代码示例
- Python Scipy stats.alpha()用法及代码示例
- Python Scipy stats.halfnorm()用法及代码示例
- Python Scipy stats.gompertz()用法及代码示例
- Python Scipy stats.genlogistic()用法及代码示例
- Python Scipy stats.fatiguelife()用法及代码示例
- Python Scipy stats.fisk()用法及代码示例
- Python Scipy stats.tmean()用法及代码示例
- Python Scipy stats.genexpon()用法及代码示例
- Python Scipy stats.genpareto()用法及代码示例
- Python Scipy stats.mean()用法及代码示例
- Python Scipy stats.gumbel_r()用法及代码示例
注:本文由纯净天空筛选整理自vishal3096大神的英文原创作品 scipy stats.beta() | Python。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
