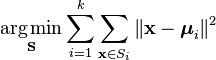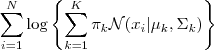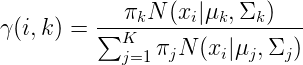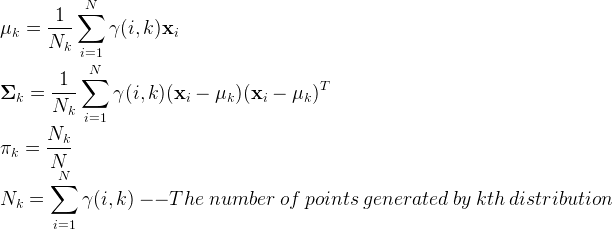当前位置: 首页>>机器学习>>正文

Spark机器学习库指南[Spark 1.3.1版]——聚类(Clustering)

@ ▣机器学习, 算法&结构 ♢, , , , , ,

下面是章节聚类的内容(其他内容参见全文目录)

聚类是一个无监督学习问题，我们基于相似的特性将数据分组成多个子集。聚类通常用于探索性分析或者作为分层监督学习管道（每个簇训练不同的分类或者回归模型）的组件。

MLlib支持下面的几个模型：

K均值(K-means)

K均值(k-means)是最通用的聚类算法之一，该算法将数据点聚类为指定数量的簇(注：基本算法原理是随机挑选N个中心点，每轮计算所有点到中心点的距离，并将点放到最近的中心，然后均值更新中心点，然后重复上述过程直至收敛，收敛的判断依据是距离阈值)。MLLib的实现包含了 k-means++的并行计算变体，该算法也叫kmeans||。它有下列参数：

  • k 需要聚簇的数量
  • maxIterations 最大迭代次数
  • initializationMode 指定初始化的模式，可以是随机初始化也可以是k-means||初始化 （k-means||初始化不全是随机选点，而是使用一个算法使选的点尽可能分散）.
  • runs 执行K均值聚簇算法的次数  (k-means不保证能找到全局最优解，同一数据集上执行多次的话，可以返回更好的聚簇结果）。
  • initializationSteps 使用k-means|| 算法选初始点时最多迭代的次数.
  • epsilon 判定k-means是否收敛的距离阈值（聚簇中心前后两次的差值小于epsilon即达到收敛条件）

补充1：kmeans的损失函数。其中(x1, x2, …, xn)是点集，每个点是d维向量，S是聚类的k个簇,μi 是Si 中所有点的均值）。这个损失函数也叫WSSS( within set sum of square)

kmeans

 

 

补充2：kmeans++方法：

kmeans++算法的主要工作体现在种子点的选择上，基本原则是使得各个种子点之间的距离尽可能的大，但是又得排除噪声的影响。 以下为基本思路：[1]

1、从输入的数据点集合（要求有k个聚类）中随机选择一个点作为第一个聚类中心
2、对于数据集中的每一个点x，计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)
3、选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大
4、重复2和3直到k个聚类中心被选出来
5、利用这k个初始的聚类中心来运行标准的k-means算法

下面的示例可以使用PySpark Shell来测试。

在下面的示例中，首先导入并解析数据，然后使用KMeans将数据聚为2类（期望的簇数量需要作为参数传递给算法）。然后计算了WSSSE(集合内平方误差和)。我们可以通过增加k来降低这个错误评估指标。事实上，最优的k通常对应WSSSE曲线中的拐点。

from pyspark.mllib.clustering import KMeans
from numpy import array
from math import sqrt

# Load and parse the data
data = sc.textFile("data/mllib/kmeans_data.txt")
parsedData = data.map(lambda line: array([float(x) for x in line.split(' ')]))

# Build the model (cluster the data)
clusters = KMeans.train(parsedData, 2, maxIterations=10,
        runs=10, initializationMode="random")

# Evaluate clustering by computing Within Set Sum of Squared Errors
def error(point):
    center = clusters.centers[clusters.predict(point)]
    return sqrt(sum([x**2 for x in (point - center)]))

WSSSE = parsedData.map(lambda point: error(point)).reduce(lambda x, y: x + y)
print("Within Set Sum of Squared Error = " + str(WSSSE))

 

高斯混合

高斯混合模型 表达的是一种混合分布，所有点都来自于k个高斯子分布中的一个，每个点都对应一个相应的概率。在MLlib的实现中，对于给定的样本集，使用最大期望算法(EM)来引导最大似然模型。算法实现由下列参数：

  • k 目标聚簇数量
  • convergenceTol 两次迭代损失(log-likelihood)变化的容忍度.
  • maxIterations 收敛之前可以运行的最大迭代次数
  • seed 随机数的种子。

 

补充：

多维度（多分量）数据的高斯混合聚类原理：

目标函数是log似然函数(log-likelihood):

1353293351_6835

 

 

相关符号说明：

  • πk : 第k个分布被选中的概率。
  • uk:  第k个分布的均值向量(维度是d)。
  • Σk:  第k个分布的协方差矩阵(d x d的矩阵)。
  • N(xi |uk , Σk)是多分量高斯分布的概率密度函数。

1. 初始化：为πk , uk , Σk生成随机初始值。(满足约束：K个πk的和为1)

2. Expectation计算：估计样本由每个高斯分布生成的概率：对于数据x它由k个分布生成的概率为(第二个等式是D维变量的高斯密度函数)：

rik

n

 

3. 最大化似然函数：在当前这一轮迭代中， 取值如下时，似然函数最大（这些公式经过一系列的数学推导得到（省略1000字））：

lk

4. 重复2,3直至收敛。

示例

下面的示例中，首先导入并解析数据，然后使用高斯混合 将数据聚为两类。最后输出混合模型的参数。

from pyspark.mllib.clustering import GaussianMixture
from numpy import array

# Load and parse the data
data = sc.textFile("data/mllib/gmm_data.txt")
parsedData = data.map(lambda line: array([float(x) for x in line.strip().split(' ')]))

# Build the model (cluster the data)
gmm = GaussianMixture.train(parsedData, 2)

# output parameters of model
for i in range(2):
    print ("weight = ", gmm.weights[i], "mu = ", gmm.gaussians[i].mu,
        "sigma = ", gmm.gaussians[i].sigma.toArray())

幂迭代聚类 (PIC)

对于图的顶点聚类（顶点相似度作为边的属性）问题，幂迭代聚类(PIC)是高效并且易扩展的算法（参考： Lin and Cohen, Power Iteration Clustering）。MLlib包含了一个使用GraphX(MLlib)为基础的实现。算法的输入是RDD[srcID, dstID, similarity]，输出是每个顶点对应的聚类的模型。相似度(similarity)必须是非负值。PIC假设相似度的衡量是对称的，也就是说在输入数据中，(srcID, dstID)顺序无关（例如：<1, 2, 0.1>, <2, 1, 0.1等价），但是只能出现一次。输入中没有指定相似度的点对，相似度会置0。MLlib中的PIC实现具有下列参数：

  • k:  聚簇的数量
  • maxIterations: 最大迭代次数
  • initializationMode: 初始化模式：默认值“random”，表示使用一个随机向量作为顶点的聚类属性；也可以是“degree”，表示使用归一化的相似度和（作为顶点的聚类属性）。

示例

下面的代码片段说明了如何使用MLlib中的PIC(这里是Scala版，Python版后续才会实现）

PowerIterationClustering 实现了PIC算法。它的输入是以RDD[srcId :Long, dstId: Long, similarity: Double]元组表示的关系矩阵。然后调用PowerIterationClustering.run并返回PowerIterationClusteringModel，它包含了计算出的类分配信息。

import org.apache.spark.mllib.clustering.PowerIterationClustering
import org.apache.spark.mllib.linalg.Vectors

val similarities: RDD[(Long, Long, Double)] = ...

val pic = new PowerIteartionClustering()
  .setK(3)
  .setMaxIterations(20)
val model = pic.run(similarities)

model.assignments.foreach { a =>
  println(s"${a.id} -> ${a.cluster}")
}

隐含狄利克雷分布 (LDA)

隐含狄利克雷分布(LDA) 是一个主题模型，它能够推理出一个文本文档集合的主体。LDA可以认为是一个聚类算法，原因如下：

  • 主题对应聚类中心，文档对应数据集中的样本（数据行）
  • 主题和文档都在一个特征空间中，其特征向量是词频向量。
  • 跟使用传统的距离来评估聚类不一样的是，LDA使用评估方式是一个函数，该函数基于文档如何生成的统计模型。

LDA以词频向量表示的文档集合作为输入。然后在最大似然函数上使用期望最大（EM）算法 来学习聚类。完成文档拟合之后，LDA提供：

  • Topics: 推断出的主题，每个主体是单词上的概率分布。
  • Topic distributions for documents: 对训练集中的每个文档，LDA给了一个在主题上的概率分布。

LDA参数如下：

  • k:  主题数量（或者说聚簇中心数量）
  • maxIterations: EM算法的最大迭代次数。
  • docConcentration: 文档在主题上分布的先验参数。当前必须大于1，值越大，推断出的分布越平滑。
  • topicConcentration: 主题在单词上的先验分布参数。当前必须大于1，值越大，推断出的分布越平滑。
  • checkpointInterval: 检查点间隔。maxIterations很大的时候，检查点可以帮助减少shuffle文件大小并且可以帮助故障恢复。

注意：当前在MLlib中，LDA是一个新特性，部分函数还没有实现。特别是，目前还不支持新文档的预测。另外也没有Python的API。这些功能后续会添加进来。

示例(Scala)

下面的例子中，首先导入词频向量表示的文档预料，然后使用LDA 推测文档的3个主题。最后，输出主题在单词上的概率分布。

import org.apache.spark.mllib.clustering.LDA
import org.apache.spark.mllib.linalg.Vectors

// Load and parse the data
val data = sc.textFile("data/mllib/sample_lda_data.txt")
val parsedData = data.map(s => Vectors.dense(s.trim.split(' ').map(_.toDouble)))
// Index documents with unique IDs
val corpus = parsedData.zipWithIndex.map(_.swap).cache()

// Cluster the documents into three topics using LDA
val ldaModel = new LDA().setK(3).run(corpus)

// Output topics. Each is a distribution over words (matching word count vectors)
println("Learned topics (as distributions over vocab of " + ldaModel.vocabSize + " words):")
val topics = ldaModel.topicsMatrix
for (topic <- Range(0, 3)) {
  print("Topic " + topic + ":")
  for (word <- Range(0, ldaModel.vocabSize)) { print(" " + topics(word, topic)); }
  println()
}

流式K均值

当数据以流式到达，就需要动态预测分类，每当新数据到来时要更新模型。MLlib提供了流式k均值聚类，该方法使用参数来控制数据的衰减。这个算法使用mini-batch k均值更新规则的一种泛化版本。对于每一批数据，将所有点赋给最近的簇，计算新的簇中心，然后使用下面的方法更新簇：

111

其中c
衰减可以通过使用halfLife参数指定。对于时刻t取得的数据，在t+halfLife时刻贡献度会降到0.5。

 

示例

 

下面的例子(scala)说明了如果对流式数据预测分类。

首先包含需要的类。

import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.clustering.StreamingKMeans

然后为训练和测试分别创建输入流。假设StreamingContext ssc已经创建好（参考Spark Streaming Programming Guide）。

val trainingData = ssc.textFileStream("/training/data/dir").map(Vectors.parse)
val testData = ssc.textFileStream("/testing/data/dir").map(LabeledPoint.parse)

创建以随机数方式生成中心的模型，并指定聚类数量。

val numDimensions = 3
val numClusters = 2
val model = new StreamingKMeans()
  .setK(numClusters)
  .setDecayFactor(1.0)
  .setRandomCenters(numDimensions, 0.0)

 

注册训练和测试数据流，并启动任务。每当有新数据到达的时候，输出预测的类。

model.trainOn(trainingData)
model.predictOnValues(testData.map(lp => (lp.label, lp.features))).print()

ssc.start()
ssc.awaitTermination()

当添加新文本文件的时候，聚类中心会被更新。训练点格式：[x1, x2, x3], 测试点格式(y, [x1,x2,x3])，y是类型标记。任意时间有文本放到/training/data/dir下，模型将被更新。任意时间，文本放到/testing/data/dir下预测值就会输出。对于新的数据，聚类中心会改变。

参考

[1] http://www.jb51.net/article/49395.htm

[2] http://en.wikipedia.org/wiki/Expectation%E2%80%93maximization_algorithm

[3] http://en.wikipedia.org/wiki/Maximum_likelihood

[4] http://en.wikipedia.org/wiki/Power_iteration

[5] http://blog.csdn.net/abcjennifer/article/details/8198352

本文由《纯净天空》出品。文章地址: https://vimsky.com/article/609.html，未经允许，请勿转载。