
目录
- 什么是聚类?
- 聚类如何应用于无监督学习问题?
- 簇(聚类)的性质
- 聚类在现实方案中的应用
- 了解聚类的不同评估指标
- 什么是K-Means聚类?
- 在Python中从头开始实现K-Means聚类
- K-Means算法面临的挑战
- K-Means++为K-Means聚类选择初始聚类质心
- 如何在K-Means中选择正确的聚类数量?
- 在Python中实现靠谱的K-Means聚类
什么是聚类?
让我们从一个简单的例子开始。一家银行希望向其客户提供信用卡优惠。当前,他们可以查看每个客户的详细信息,并根据此信息确定应向哪个客户提供报价。
然而,银行可能拥有数百万的客户,那么分别查看每个客户的详细信息然后做出决定是否有意义呢?当然不是!这是一个手动过程,将花费大量时间。
那么银行需要怎么做?一种不错的选择是将其客户划分为不同的组。例如,银行可以根据客户的收入对其进行分组:

银行现在可以制定三种不同的策略或提议,每个组一种。在这里,他们不必为单个客户创建不同的策略,而只需制定3个策略。这将大幅减少工作量和时间。
我上面显示的组称为簇,而创建这些组的过程称为聚类。正式地,我们可以这样说:
聚类是根据数据中的模式将整个数据分为几组(也称为簇)的过程。
那么聚类是哪种类型的学习问题?是有监督的还是无监督的学习问题?
从上述的示例,我们可以看到聚类是一个无监督的学习问题!
如何将聚类用于无监督学习问题?
假设您正在从事一个需要预测大型市场销量的项目:
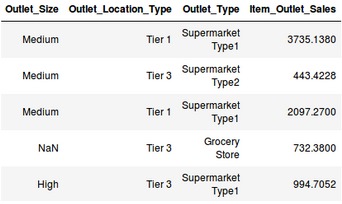
或者,您的任务是预测贷款是否会被批准的项目:
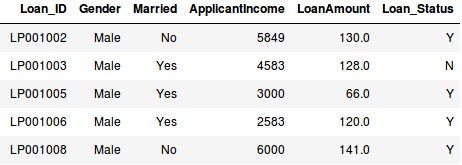
在这两种情况下,我们都有固定的预测目标。在销售预测问题中,我们必须基于outlet_size,outlet_location_type等等,预测Item_Outlet_Sales;在贷款审批问题中,我们必须基于性别,婚姻状况,客户收入等,预测Loan_Status。
因此,当我们有一个目标变量,并根据给定的一组自变量进行预测时,此类问题称为监督学习问题。
然而,有些情况下我们会没有任何目标变量可以观测到。
没有任何固定目标变量的学习问题称为无监督学习问题。在这些问题中,我们只有自变量,而没有目标/因变量。
而在聚类中,我们没有可预测的目标。我们需要尝试合并相似的观察结果来形成不同的组。因此,这是一个无监督的学习问题。
现在我们知道什么是簇以及聚类的概念。接下来,让我们看看在形成簇时必须考虑的这些簇的属性。
簇(聚类)的性质
还是以之前银行细分客户的任务为例。为简单起见,假设银行只希望使用收入和债务进行细分。他们收集了客户数据,并使用散点图将其可视化:
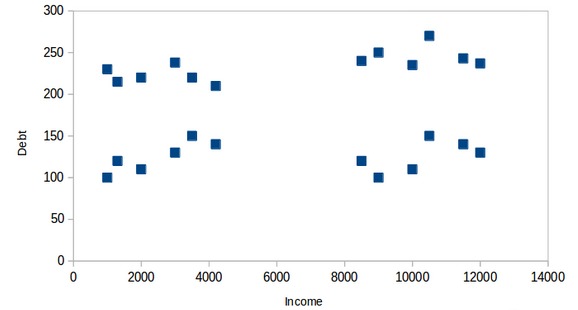
在X轴上,我们有客户的收入,而y轴代表债务的金额。在这里,我们可以清楚地看到这些客户可以分为四个不同的簇,如下图所示:
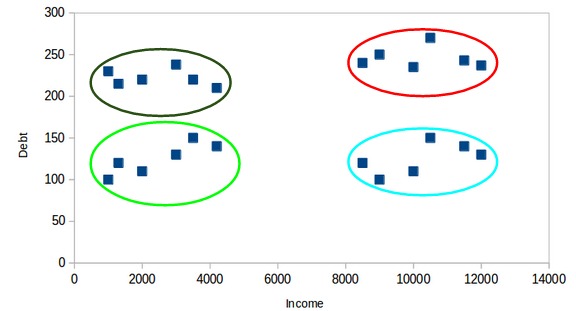
这就是聚类如何帮助从数据创建细分(簇)的方式。银行可以进一步使用这些簇来制定策略并为其客户提供折扣。接下来,让我们看一下这些簇(聚类)必须具备的属性。
属性1
簇(聚类)中的所有数据点应彼此相似。以上面的示例进行说明:
如果特定簇中的客户彼此不同,那么他们的要求可能会有所不同,对吧?而如果银行给他们相同的报价,他们可能会不喜欢。
只有同一个簇中数据点相似,才有助于银行使用它来做定向营销。
属性2
来自不同簇的数据点应尽可能不同。让我们再次前述示例来了解此属性:
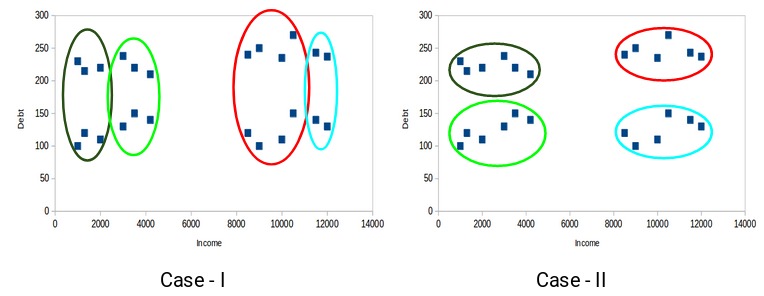
您认为以下哪种情况算作更好的聚类簇?如果您看案例I:
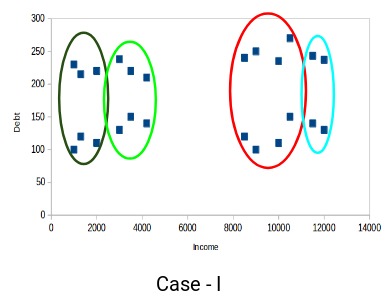
红色和蓝色簇中的客户彼此非常相似。红色簇中的前四个点(客户)与蓝色簇中的前两个客户具有相似的属性。他们有高收入和高债务的特点。而在这里,我们将它们划到不同的簇(聚类)。而如果您看案例II:
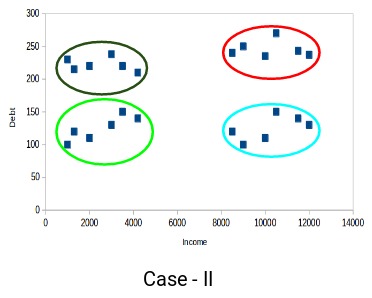
红色簇中的点(客户)与蓝色簇中的客户完全不同。红色簇中的所有客户都具有高收入和高债务,蓝色簇中的所有客户都具有高收入和低债务。显然,在这种聚类情况下,我们拥有更好的客户分群。
因此,来自不同簇的数据点应尽可能彼此不同。
到目前为止,我们已经了解了什么是聚类以及聚类的不同属性。接下来,我们研究聚类的一些应用。
聚类在真实方案中的应用
聚类是业界广泛使用的技术。实际上,它几乎在每个领域中都有使用,从银行业务到推荐引擎,文档聚类到图像分割。
客户细分
我们已经在前面进行了介绍——聚类的最常见应用之一是客户细分。而且不仅限于银行业务。该策略涉及多个领域,包括电信、电子商务、体育、广告、销售等。
文件聚类
这是聚类的另一个常见应用。假设您有多个文档,并且需要将相似的文档聚在一起。聚类可以帮助我们将这些文档分组,以使相似的文档位于同一簇中。

图像分割
我们还可以使用聚类来执行图像分割。在这里,我们尝试将图像中相似的像素合并在一起。我们可以应用聚类来创建在同一组中具有相似像素的聚类。

你可以参考本文了解如何利用聚类进行图像分割任务。
推荐引擎
聚类也可以用于推荐引擎。假设您想向朋友推荐歌曲。您可以查看Ta喜欢的歌曲,然后使用聚类法找到相似的歌曲,最后推荐这些相似歌曲。
接下来,让我们看一下如何评估聚类效果。
了解聚类的不同评估指标
聚类的主要目的不只是建立簇,而是建立良好且有意义的簇。我们在以下示例中看到了这一点:

在这里,我们仅使用了两个特征维度,因此我们很容易可视化并确定这些聚类哪个更好。
不幸的是,这不是现实方案的工作方式,现实中将有大量特征(高维)。让我们再次以客户细分为例——我们将提供客户的收入,职业,性别,年龄等特征。将所有这些特征一起可视化并确定更好和有意义的簇对我们来说是不可能的。
这就是我们为什么需要使用评估指标的地方,因为你没法通过肉眼判断聚类的好坏了。让我们讨论部分评估指标,以了解如何使用它们来评估集群的质量。
惯性
回想一下我们上面介绍的聚类簇的第一个属性,其实就是惯性评估的结果,它告诉我们簇中的点彼此有多远。所以,惯性实际上是计算簇中所有点跟簇的质心的距离总和。
簇内的距离也叫类内距离。因此,惯性给我们提供了类内距离的总和:
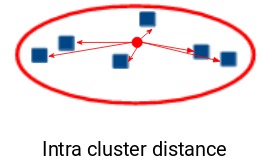
现在,您认为一个好的簇的惯性值应该是多少?较小的惯性值是好的还是更大的值?我们希望同一聚类中的点彼此相似,对吗?因此,它们之间的距离应尽可能短。
牢记这一点,我们可以说惯性值越小,我们的簇越好。
邓恩指数(Dunn Index)
如果一个簇的质心与该簇中的点之间的距离很小,则意味着这些点彼此靠近。因此,惯性确保满足簇的第一个属性。但是,它并不关心第二个属性-不同的簇应尽可能彼此不同。
这就是邓恩指数可以起作用的地方。
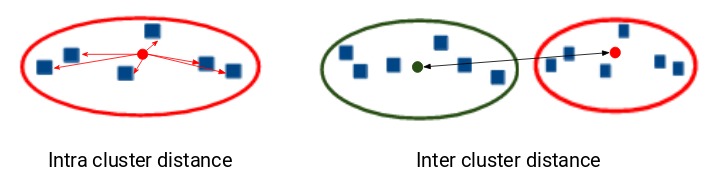
除了簇的质心和簇内点之间的距离之外,邓恩指数还考虑了两个簇之间的距离。两个不同簇的质心之间的距离称为类间(inter-cluster)距离。让我们看一下邓恩指数的公式:
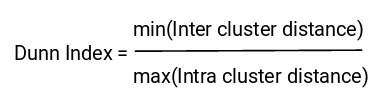
Dunn Index是类间最小距离与类内最大距离之比。
我们要最大化邓恩指数。 Dunn Index的值越大,聚类就越好。我们看下邓恩指数背后的直觉:

为了最大化Dunn Index的值,分子应为最大值。在这里,我们采用类间(inter-cluster)距离中的最小值。因此,即使是最接近的簇之间的距离也应该更大,这最终将确保簇之间的距离较远。

同样,分母应最小以最大化Dunn Index。在这里,我们采用最大的类内距离。簇的质心和点之间的最大距离应最小,这将确保簇是紧凑的。
K-Means聚类简介
我们终于到了本文的重点!
回想一下聚类的第一个属性-它指出聚类中的点应该彼此相似。所以,我们的目标是使聚类簇中的点之间的距离最小。
k-means聚类技术——一种试图将簇的质心到点的距离最小化的算法。
K-means是基于质心的算法或基于距离的算法,我们在其中计算将点分配给某个簇的距离。在K-Means中,每个聚类簇与一个质心关联。
K-Means算法的主要目标是最小化所有点与它们各自的聚类质心之间的距离之和。
现在让我们来看一个例子,以了解K-Means的实际工作原理:

有以上这8个点,我们想应用k-means为这些点创建聚类簇。方法如下:
步骤1:选择聚类簇数量k
k-means的第一步是选择聚类数k。
步骤2:从数据中选择k个随机点作为质心
接下来,我们为每个簇随机选择质心。假设我们需要2个簇,因此k等于2。然后,我们随机选择质心:

在这里,红色和绿色圆圈分别代表这2个簇的质心。
步骤3:将所有点分配给最近的聚类质心
初始化质心后,我们将每个点分配给最近的聚类质心:
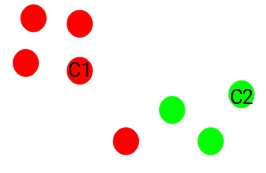
在这里,您可以看到将接近红点的点分配给红色簇,而将接近绿点的点分配给绿色簇。
步骤4:重新计算新形成的簇的质心
现在,将所有点分配给任一簇后,下一步是计算新形成的簇的质心:
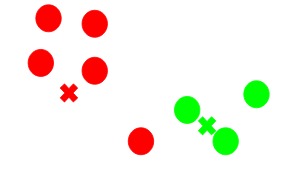
在这里,红色和绿色的十字叉是新的质心。
步骤5:重复步骤3和4
然后,我们重复步骤3和4:

计算质心并将所有点基于它们与质心的距离分配给簇的步骤,这只是一次迭代。那我们何时应停止此过程?
K-Means聚类的停止条件
基本上可以采用三种停止标准来终止K-means算法:
- 前后两次迭代新形成的簇的质心不变
- 前后两次迭代点保持在同一簇中
- 达到最大迭代次数
简单解读下3个标准:
如果新形成的簇的质心没有改变,我们可以停止算法。
另一个明确的信号是,在对算法进行多次迭代训练之后,如果点仍在同一簇中,我们也应停止训练过程。
最后,如果达到最大迭代次数,我们可以停止训练。假设我们将迭代次数设置为100。在停止之前,该过程将重复100次迭代。
在Python中从头开始实现K-Means聚类[初级版]
是时候启动我们的Jupyter Notebook(或您使用的其他任何IDE)并用Python来试水开发了!
我们将使用这个大型集市销售数据集,点这里下载。我鼓励您阅读有关数据集和问题陈述的更多信息(见这里)。这将有助于您理解我们正在做什么(以及为什么要这样做)。
首先,导入所有必需的库:
#import libraries
import pandas as pd
import numpy as np
import random as rd
import matplotlib.pyplot as plt现在,我们将读取CSV文件,并查看数据的前五行:
data = pd.read_csv('clustering.csv')
data.head()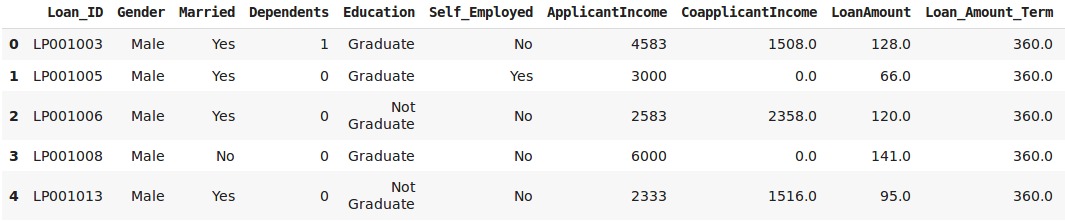
对于本文,我们仅从数据中获取两个变量-“LoanAmount”和“ApplicantIncome”。这样简化处理,数据的可视化更容易。我们选择这两个变量并可视化数据点:
X = data[["LoanAmount","ApplicantIncome"]]
#Visualise data points
plt.scatter(X["ApplicantIncome"],X["LoanAmount"],c='black')
plt.xlabel('AnnualIncome')
plt.ylabel('Loan Amount (In Thousands)')
plt.show()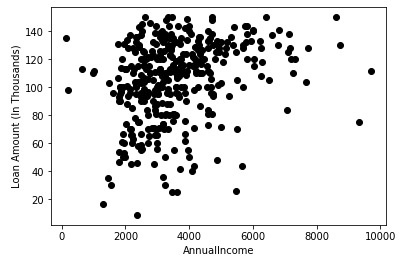
对于K-Means的步骤1和2,关于选择簇数(k)并为每个簇选择随机质心——我们将选择3个聚类,然后从数据中选择随机观测值作为质心:
# Step 1 and 2 - Choose the number of clusters (k) and select random centroid for each cluster#number of clusters
K=3
# Select random observation as centroids
Centroids = (X.sample(n=K))
plt.scatter(X[“ApplicantIncome”],X[“LoanAmount”],c=’black’)
plt.scatter(Centroids[“ApplicantIncome”],Centroids[“LoanAmount”],c=’red’)
plt.xlabel(‘AnnualIncome’)
plt.ylabel(‘Loan Amount (In Thousands)’)
plt.show()

在这里,3个红点分别代表3个簇质心。请注意,我们是随机选择这些点的,因此,每次运行此代码时,您可能会得到不同的质心。
接下来,我们将定义一些条件来实现K-Means聚类算法。首先看一下代码:
# Step 3 - Assign all the points to the closest cluster centroid
# Step 4 - Recompute centroids of newly formed clusters
# Step 5 - Repeat step 3 and 4
diff = 1
j=0
while(diff!=0):
XD=X
i=1
for index1,row_c in Centroids.iterrows():
ED=[]
for index2,row_d in XD.iterrows():
d1=(row_c["ApplicantIncome"]-row_d["ApplicantIncome"])**2
d2=(row_c["LoanAmount"]-row_d["LoanAmount"])**2
d=np.sqrt(d1+d2)
ED.append(d)
X[i]=ED
i=i+1
C=[]
for index,row in X.iterrows():
min_dist=row[1]
pos=1
for i in range(K):
if row[i+1] < min_dist:
min_dist = row[i+1]
pos=i+1
C.append(pos)
X["Cluster"]=C
Centroids_new = X.groupby(["Cluster"]).mean()[["LoanAmount","ApplicantIncome"]]
if j == 0:
diff=1
j=j+1
else:
diff = (Centroids_new['LoanAmount'] - Centroids['LoanAmount']).sum() + (Centroids_new['ApplicantIncome'] - Centroids['ApplicantIncome']).sum()
print(diff.sum())
Centroids = X.groupby(["Cluster"]).mean()[["LoanAmount","ApplicantIncome"]]
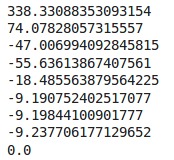
注意:因为有随机选择质心操作,每次我们运行这些值时,结果可能跟上图有所不同。在这里,当质心在两次迭代后没有变化时,我们将停止训练。我们最初定义了diff=1,在while循环中,我们计算前一次迭代与当前迭代中质心之间的差异作为diff。
当此差为0时,我们将停止训练。现在,让我们可视化结果簇:
color=['blue','green','cyan']
for k in range(K):
data=X[X["Cluster"]==k+1]
plt.scatter(data["ApplicantIncome"],data["LoanAmount"],c=color[k])
plt.scatter(Centroids["ApplicantIncome"],Centroids["LoanAmount"],c='red')
plt.xlabel('Income')
plt.ylabel('Loan Amount (In Thousands)')
plt.show()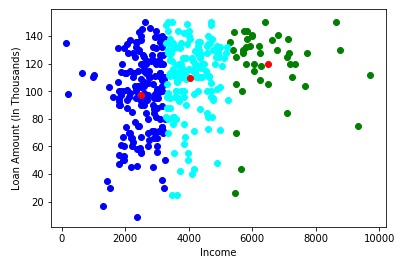
很漂亮的结果!在这里,我们可以清晰地可视化三个群集。红点代表每个簇的质心。希望您现在对K-Means的工作方式有清楚的了解。
但是,在某些情况下,该算法可能无法很好地执行。让我们看看使用k-means时可能会遇到的一些挑战。
K-Means聚类算法面临的挑战
使用K-Means时,我们面临的常见挑战之一是簇的大小不同。假设我们有以下几点:
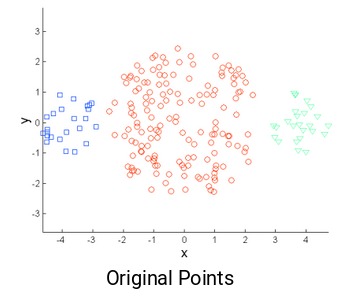
与中间的簇相比,最左侧和最右侧的簇较小。如果在这些点上应用k-means聚类,结果将是这样的:
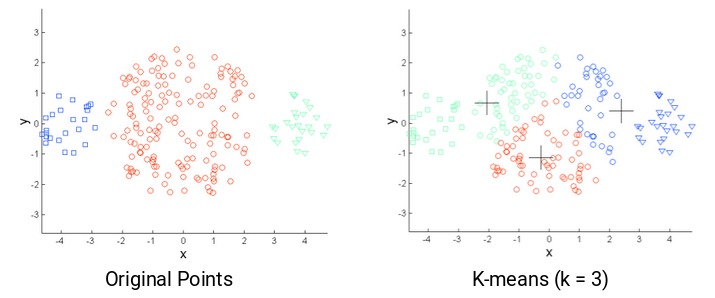
k-means的另一个挑战是原始点的密度不同。假设这些是原始点:
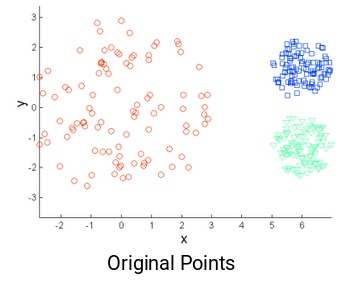
图中,红色簇中的点散开,而其余簇中的点紧密堆积在一起。如果在这些点上应用k-means,我们将获得如下所示的聚类:
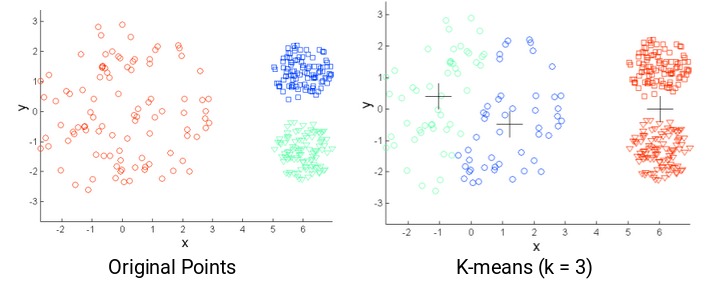
我们可以看到,2个紧促的簇已分配给单个簇。而位于同一簇中的点已分配给不同的簇。结果很不理想,该怎么办?
解决方案之一是使用更多数量的簇。因此,在上述几种情况下,我们可以使用更大的簇数量,而不是使用3个簇。也许设置k = 10可能会获得更有意义的聚类簇。
还记得我们如何在k-means聚类中随机初始化质心吗?嗯,这也是潜在的问题,因为我们每次都可能获得不同的簇。因此,为了解决随机初始化的问题,有一种算法称为K-Means++,它可用于选择K-Means的初始值后者说初始簇质心。
K-Means++为K-Means聚类选择初始聚类质心
在某些情况下,如果簇的初始化不合适,则K-Means可能会得到糟糕的聚类。这是K-Means ++产生的原因,它指定了在使用标准k-means聚类算法进行操作之前初始化聚类中心的过程。
在使用K-Means ++初始化时,我们更有可能找到与理想情况最佳K-Means解决方案接近的解决方案。
使用K-Means ++初始化质心的步骤为:
- 从我们要聚类的数据点中随机选择第一个聚类。这类似于我们在K-Means中所做的操作,但是我们不是在随机选择所有质心,而是在此处选择一个质心
- 接下来,我们计算每个数据点(x)与已经选择的聚类中心的距离(D(x))
- 然后,从数据点选择新的聚类中心,其中点x选到作为新质心的概率与(D(x))^2成正比(即与距离的平方成正比)
- 然后,我们重复步骤2和3,直到已选择K个簇心
下面举个例子来更清楚地了解这一点。假设我们有以下几点,我们想在这里建立3个聚类:

第一步是随机选择一个数据点作为聚类质心:

假设我们选择绿点作为初始质心。现在,我们将计算此质心到每个数据点的距离(D(x)):
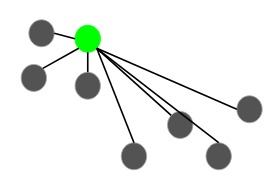
下一个质心将是其平方距离(D(x)^2)最大即离当前质心最远的那个:

也就是说,红点将被选作下一个质心。然后,要选择最后一个质心,我们计算每个点与其最近的质心的距离,并选择平方距最大的点作为下一个质心:
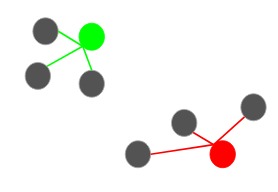
我们将最后一个质心选择为蓝色点:

初始化质心后,使用标准K-Means算法即可。使用K-Means ++初始化质心会改善聚类效果。虽然相对于随机初始化,它的计算成本很高,但随后的K-Means收敛速度通常更快。
接下来的问题是-我们应该聚类为几个簇?也就是说,执行K-Means时,簇的最佳数目应该是多少?
如何为K-Means聚类选择正确的簇数量?
使用K-Means时,最普遍的疑问之一就是如何选择正确的簇数量。
这里介绍一种技术,该技术帮助我们为K-Means算法选择正确的簇值。还是以前面看到的客户细分为例。回顾一下,该银行希望根据客户的收入和债务金额对其客户进行细分:

在这里,我们可以用2聚类将客户分开,如下所示:

所有低收入客户都在一个簇中,而高收入客户都在第二个簇中。我们还可以有4个聚类:
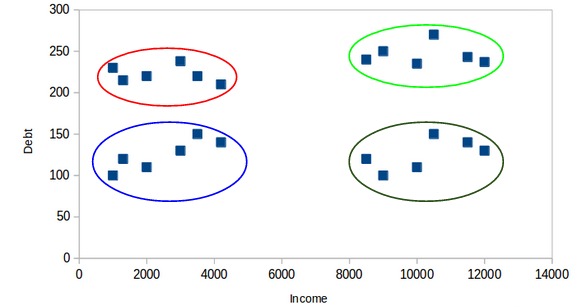
在这里,一个簇可能代表低收入和低负债的客户,另一个簇可能是那些高收入,高负债的客户,依此类推。当然,也可以有8个簇:
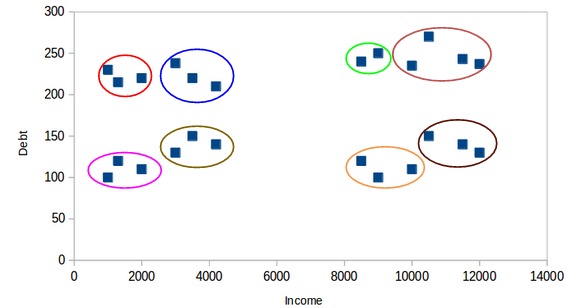
实际上,我们可以有任意数量的簇。最极端的情况,可以把每个点分配给一个单独的簇。在这种情况下,聚类簇的数量将等于观测点的数量。所以,
聚类的最大可能数目将等于数据集中的观测点数目。
但是,我们如何才能确定最佳的簇数呢?我们可以做的是绘制一个图,也称为弯头曲线,其中x轴将代表簇的数量,而y轴为评估指标(比如说:惯性)。
当然,您还可以选择任何其他评估指标,例如邓恩指数(Dunn Index):

接下来,我们将从一个小的簇数开始,比如说2。使用2个簇训练模型,计算该模型的惯性,最后将其绘制在上图中。假设我们的惯性值约为1000:

现在,我们将增加簇的数量,再次训练模型,并绘制惯性值。得到的曲线图如下:
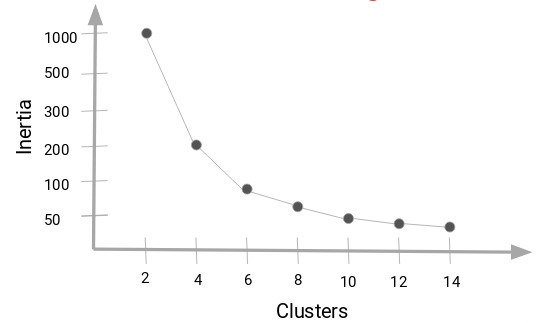
当我们将簇值从2更改为4时,惯性值会急剧下降。随着我们进一步增加簇的数量,惯性值将减小并最终变为恒定值。所以,
可以将惯性值的减小变为恒定的聚类值作为我们数据的正确聚类值。
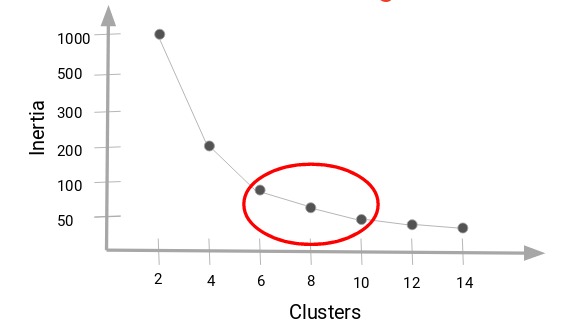
在这里,我们可以选择6到10之间的任意值作为簇数。在确定聚类簇数时,还必须考虑计算成本。如果我们增加聚类的数量,计算成本也会增加。因此,如果您没有大量的计算资源,我的建议是选择数量较少的簇数。
接下来,我们在Python使用算法库实现真正的K-Means聚类算法。我们还将看到如何使用K-Means++初始化质心,并且绘制出弯头曲线以决定数据集上合适的聚类数量。
在Python中实现K-Means集群[算法库库版】
我们将致力于解决批发客户细分问题。您可以使用这个连结下载数据集。数据托管在UCI机器学习存储库中。
此问题的目的是根据批发分销商的客户每年在各种产品类别(如牛奶,杂货,地区等)上的支出进行细分。接下来,看代码吧!
首先导入所需的库:
# importing required libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.cluster import KMeans接下来,加载数据并查看前五行:
# reading the data and looking at the first five rows of the data
data=pd.read_csv("Wholesale customers data.csv")
data.head()
我们拥有客户在牛奶,杂货,冷冻,洗涤剂等不同产品上的支出明细。然后,我们必须根据提供的明细对客户进行细分。在此之前,我们先提取一些与数据有关的统计信息:
# statistics of the data
data.describe()
在这里,我们看到数据大小存在很多变化。渠道和区域等变量的幅度较小,而鲜食,牛奶,杂货等变量的幅度较高。
由于K-Means是基于距离的算法,因此,这种幅度上的差异会产生问题。因此,首先标准化变量达到相同的尺度:
# standardizing the data
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)# statistics of scaled data
pd.DataFrame(data_scaled).describe()

现在的大小看起来相似。接下来,让我们创建一个kmeans模型并将其拟合到数据上:
# defining the kmeans function with initialization as k-means++
kmeans = KMeans(n_clusters=2, init='k-means++')# fitting the k means algorithm on scaled data
kmeans.fit(data_scaled)
我们初始化了两个簇。注意:初始化在这里不是随机的,我们使用了k-means ++初始化,这通常会产生更好的结果,正如我们在上一节中所讨论的那样。
接下来评估形成的簇效果。为此,我们将计算聚类的惯性:
# inertia on the fitted data
kmeans.inertia_输出:2599.38555935614
我们得到的惯性值几乎为2600。现在,让我们看看如何使用弯头曲线来确定最佳簇数。
首先拟合多个k-means模型: 每个聚类模型使用不同的簇数量,簇数量依次增加。计算每个模型的惯性值,然后将其绘制以可视化结果:
# fitting multiple k-means algorithms and storing the values in an empty list
SSE = []
for cluster in range(1,20):
kmeans = KMeans(n_jobs = -1, n_clusters = cluster, init='k-means++')
kmeans.fit(data_scaled)
SSE.append(kmeans.inertia_)# converting the results into a dataframe and plotting them
frame = pd.DataFrame({‘Cluster’:range(1,20), ‘SSE’:SSE})
plt.figure(figsize=(12,6))
plt.plot(frame[‘Cluster’], frame[‘SSE’], marker=’o’)
plt.xlabel(‘Number of clusters’)
plt.ylabel(‘Inertia’)
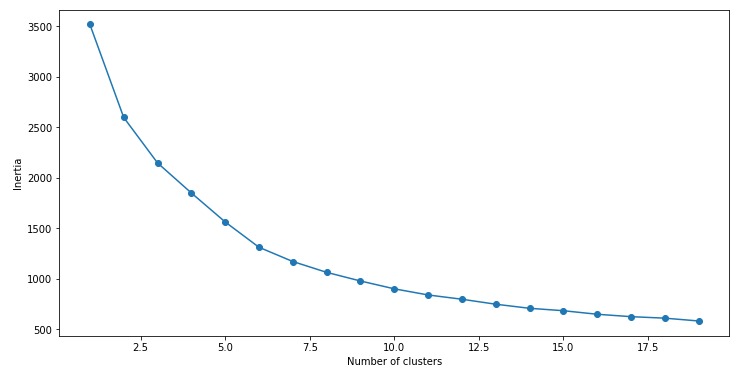
您能从该图中得知最佳聚类值吗?看上面的肘弯,我们可以选择5到8之间的任意数量的聚类簇值。比如我们将簇数设置为6并拟合模型:
# k means using 5 clusters and k-means++ initialization
kmeans = KMeans(n_jobs = -1, n_clusters = 5, init='k-means++')
kmeans.fit(data_scaled)
pred = kmeans.predict(data_scaled)最后,让我们看一下每个上述聚类中的点数计数:
frame = pd.DataFrame(data_scaled)
frame['cluster'] = pred
frame['cluster'].value_counts()
可以看到,属于聚类4的有234个数据点(索引3),然后属于聚类2的有125个数据点(索引1),依此类推。
以上就是我们如何在Python中实现K-Means聚类的方法。
尾注
在本文中,我们讨论了最著名的聚类算法之一——K-Means。我们从头开始实现Kmens算法,并研究了一步一步如何实现。另外,也探讨了使用K-Means时可能面临的挑战,并介绍了K-Means ++在初始化聚类质心时如何提供帮助。
最后,我们实现了Python版本的k-means,并绘制了弯头曲线,该曲线有助于在K-Means算法中找到最佳的簇数。
