目錄

1. 什麽是聚類？
2. 聚類如何應用於無監督學習問題？
3. 簇(聚類)的性質
4. 聚類在現實方案中的應用
5. 了解聚類的不同評估指標
6. 什麽是K-Means聚類？
7. 在Python中從頭開始實現K-Means聚類
8. K-Means算法麵臨的挑戰
9. K-Means++為K-Means聚類選擇初始聚類質心
10. 如何在K-Means中選擇正確的聚類數量？
11. 在Python中實現靠譜的K-Means聚類

什麽是聚類？

讓我們從一個簡單的例子開始。一家銀行希望向其客戶提供信用卡優惠。當前，他們可以查看每個客戶的詳細信息，並根據此信息確定應向哪個客戶提供報價。

然而，銀行可能擁有數百萬的客戶，那麽分別查看每個客戶的詳細信息然後做出決定是否有意義呢？當然不是！這是一個手動過程，將花費大量時間。

那麽銀行需要怎麽做？一種不錯的選擇是將其客戶劃分為不同的組。例如，銀行可以根據客戶的收入對其進行分組：

銀行現在可以製定三種不同的策略或提議，每個組一種。在這裏，他們不必為單個客戶創建不同的策略，而隻需製定3個策略。這將大幅減少工作量和時間。

我上麵顯示的組稱為簇，而創建這些組的過程稱為聚類。正式地，我們可以這樣說：

聚類是根據數據中的模式將整個數據分為幾組(也稱為簇)的過程。

那麽聚類是哪種類型的學習問題？是有監督的還是無監督的學習問題？

從上述的示例，我們可以看到聚類是一個無監督的學習問題！

如何將聚類用於無監督學習問題？

假設您正在從事一個需要預測大型市場銷量的項目：

或者，您的任務是預測貸款是否會被批準的項目：

在這兩種情況下，我們都有固定的預測目標。在銷售預測問題中，我們必須基於outlet_size，outlet_location_type等等，預測Item_Outlet_Sales；在貸款審批問題中，我們必須基於性別，婚姻狀況，客戶收入等，預測Loan_Status。

因此，當我們有一個目標變量，並根據給定的一組自變量進行預測時，此類問題稱為監督學習問題。

然而，有些情況下我們會沒有任何目標變量可以觀測到。

沒有任何固定目標變量的學習問題稱為無監督學習問題。在這些問題中，我們隻有自變量，而沒有目標/因變量。

而在聚類中，我們沒有可預測的目標。我們需要嘗試合並相似的觀察結果來形成不同的組。因此，這是一個無監督的學習問題。

現在我們知道什麽是簇以及聚類的概念。接下來，讓我們看看在形成簇時必須考慮的這些簇的屬性。

簇(聚類)的性質

還是以之前銀行細分客戶的任務為例。為簡單起見，假設銀行隻希望使用收入和債務進行細分。他們收集了客戶數據，並使用散點圖將其可視化：

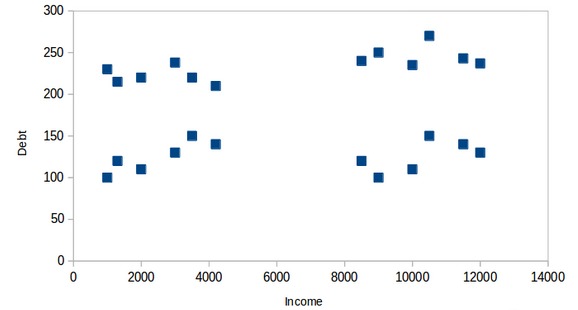
在X軸上，我們有客戶的收入，而y軸代表債務的金額。在這裏，我們可以清楚地看到這些客戶可以分為四個不同的簇，如下圖所示：

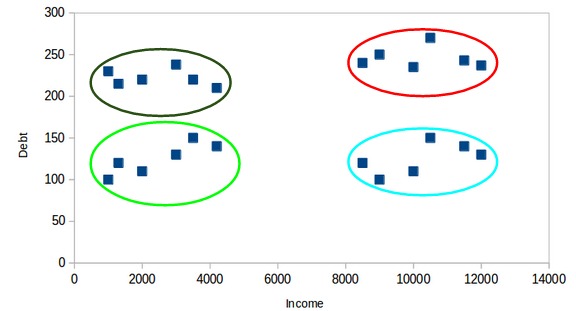
這就是聚類如何幫助從數據創建細分(簇)的方式。銀行可以進一步使用這些簇來製定策略並為其客戶提供折扣。接下來，讓我們看一下這些簇(聚類)必須具備的屬性。

屬性1

簇(聚類)中的所有數據點應彼此相似。以上麵的示例進行說明：

如果特定簇中的客戶彼此不同，那麽他們的要求可能會有所不同，對吧？而如果銀行給他們相同的報價，他們可能會不喜歡。

隻有同一個簇中數據點相似，才有助於銀行使用它來做定向營銷。

屬性2

來自不同簇的數據點應盡可能不同。讓我們再次前述示例來了解此屬性：

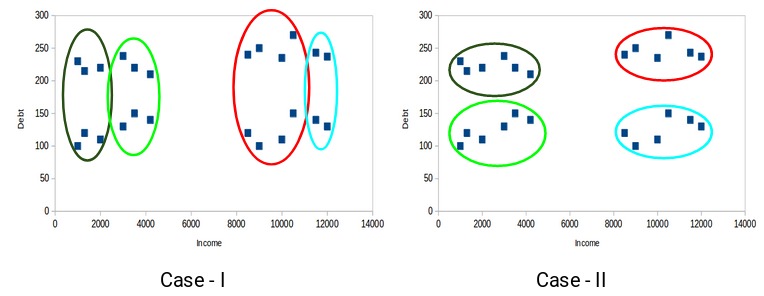
您認為以下哪種情況算作更好的聚類簇？如果您看案例I：

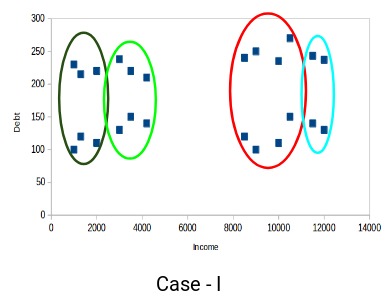
紅色和藍色簇中的客戶彼此非常相似。紅色簇中的前四個點(客戶)與藍色簇中的前兩個客戶具有相似的屬性。他們有高收入和高債務的特點。而在這裏，我們將它們劃到不同的簇(聚類)。而如果您看案例II：

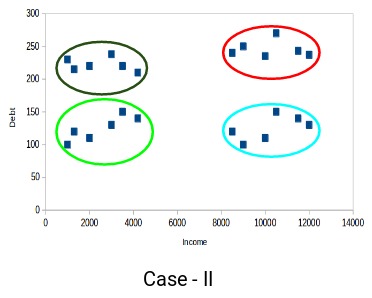
紅色簇中的點(客戶)與藍色簇中的客戶完全不同。紅色簇中的所有客戶都具有高收入和高債務，藍色簇中的所有客戶都具有高收入和低債務。顯然，在這種聚類情況下，我們擁有更好的客戶分群。

因此，來自不同簇的數據點應盡可能彼此不同。

到目前為止，我們已經了解了什麽是聚類以及聚類的不同屬性。接下來，我們研究聚類的一些應用。

聚類在真實方案中的應用

聚類是業界廣泛使用的技術。實際上，它幾乎在每個領域中都有使用，從銀行業務到推薦引擎，文檔聚類到圖像分割。

客戶細分

我們已經在前麵進行了介紹——聚類的最常見應用之一是客戶細分。而且不僅限於銀行業務。該策略涉及多個領域，包括電信、電子商務、體育、廣告、銷售等。

文件聚類

這是聚類的另一個常見應用。假設您有多個文檔，並且需要將相似的文檔聚在一起。聚類可以幫助我們將這些文檔分組，以使相似的文檔位於同一簇中。

圖像分割

我們還可以使用聚類來執行圖像分割。在這裏，我們嘗試將圖像中相似的像素合並在一起。我們可以應用聚類來創建在同一組中具有相似像素的聚類。

你可以參考本文了解如何利用聚類進行圖像分割任務。

推薦引擎

聚類也可以用於推薦引擎。假設您想向朋友推薦歌曲。您可以查看Ta喜歡的歌曲，然後使用聚類法找到相似的歌曲，最後推薦這些相似歌曲。

接下來，讓我們看一下如何評估聚類效果。

了解聚類的不同評估指標

聚類的主要目的不隻是建立簇，而是建立良好且有意義的簇。我們在以下示例中看到了這一點：

在這裏，我們僅使用了兩個特征維度，因此我們很容易可視化並確定這些聚類哪個更好。

不幸的是，這不是現實方案的工作方式，現實中將有大量特征(高維)。讓我們再次以客戶細分為例——我們將提供客戶的收入，職業，性別，年齡等特征。將所有這些特征一起可視化並確定更好和有意義的簇對我們來說是不可能的。

這就是我們為什麽需要使用評估指標的地方，因為你沒法通過肉眼判斷聚類的好壞了。讓我們討論部分評估指標，以了解如何使用它們來評估集群的質量。

慣性

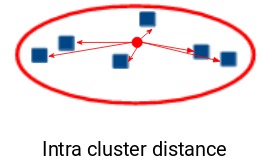
回想一下我們上麵介紹的聚類簇的第一個屬性，其實就是慣性評估的結果，它告訴我們簇中的點彼此有多遠。所以，慣性實際上是計算簇中所有點跟簇的質心的距離總和。

簇內的距離也叫類內距離。因此，慣性給我們提供了類內距離的總和：

現在，您認為一個好的簇的慣性值應該是多少？較小的慣性值是好的還是更大的值？我們希望同一聚類中的點彼此相似，對嗎？因此，它們之間的距離應盡可能短。

牢記這一點，我們可以說慣性值越小，我們的簇越好。

鄧恩指數(Dunn Index)

如果一個簇的質心與該簇中的點之間的距離很小，則意味著這些點彼此靠近。因此，慣性確保滿足簇的第一個屬性。但是，它並不關心第二個屬性-不同的簇應盡可能彼此不同。

這就是鄧恩指數可以起作用的地方。

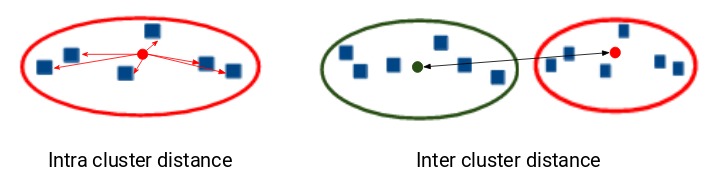
除了簇的質心和簇內點之間的距離之外，鄧恩指數還考慮了兩個簇之間的距離。兩個不同簇的質心之間的距離稱為類間(inter-cluster)距離。讓我們看一下鄧恩指數的公式：

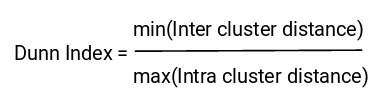
Dunn Index是類間最小距離與類內最大距離之比。

我們要最大化鄧恩指數。 Dunn Index的值越大，聚類就越好。我們看下鄧恩指數背後的直覺：

為了最大化Dunn Index的值，分子應為最大值。在這裏，我們采用類間(inter-cluster)距離中的最小值。因此，即使是最接近的簇之間的距離也應該更大，這最終將確保簇之間的距離較遠。

同樣，分母應最小以最大化Dunn Index。在這裏，我們采用最大的類內距離。簇的質心和點之間的最大距離應最小，這將確保簇是緊湊的。

K-Means聚類簡介

我們終於到了本文的重點！

回想一下聚類的第一個屬性-它指出聚類中的點應該彼此相似。所以，我們的目標是使聚類簇中的點之間的距離最小。

k-means聚類技術——一種試圖將簇的質​​心到點的距離最小化的算法。

K-means是基於質心的算法或基於距離的算法，我們在其中計算將點分配給某個簇的距離。在K-Means中，每個聚類簇與一個質心關聯。

K-Means算法的主要目標是最小化所有點與它們各自的聚類質心之間的距離之和。

現在讓我們來看一個例子，以了解K-Means的實際工作原理：

有以上這8個點，我們想應用k-means為這些點創建聚類簇。方法如下：

步驟1：選擇聚類簇數量k

k-means的第一步是選擇聚類數k。

步驟2：從數據中選擇k個隨機點作為質心

接下來，我們為每個簇隨機選擇質心。假設我們需要2個簇，因此k等於2。然後，我們隨機選擇質心：

在這裏，紅色和綠色圓圈分別代表這2個簇的質心。

步驟3：將所有點分配給最近的聚類質心

初始化質心後，我們將每個點分配給最近的聚類質心：

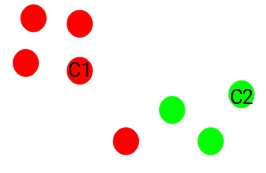
在這裏，您可以看到將接近紅點的點分配給紅色簇，而將接近綠點的點分配給綠色簇。

步驟4：重新計算新形成的簇的質心

現在，將所有點分配給任一簇後，下一步是計算新形成的簇的質心：

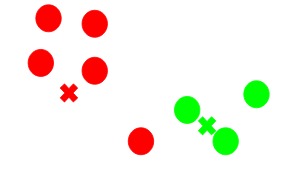
在這裏，紅色和綠色的十字叉是新的質心。

步驟5：重複步驟3和4

然後，我們重複步驟3和4：

計算質心並將所有點基於它們與質心的距離分配給簇的步驟，這隻是一次迭代。那我們何時應停止此過程？

K-Means聚類的停止條件

基本上可以采用三種停止標準來終止K-means算法：

1. 前後兩次迭代新形成的簇的質心不變
2. 前後兩次迭代點保持在同一簇中
3. 達到最大迭代次數

簡單解讀下3個標準：

如果新形成的簇的質心沒有改變，我們可以停止算法。

另一個明確的信號是，在對算法進行多次迭代訓練之後，如果點仍在同一簇中，我們也應停止訓練過程。

最後，如果達到最大迭代次數，我們可以停止訓練。假設我們將迭代次數設置為100。在停止之前，該過程將重複100次迭代。

在Python中從頭開始實現K-Means聚類[初級版]

是時候啟動我們的Jupyter Notebook(或您使用的其他任何IDE)並用Python來試水開發了！

我們將使用這個大型集市銷售數據集，點這裏下載。我鼓勵您閱讀有關數據集和問題陳述的更多信息(見這裏)。這將有助於您理解我們正在做什麽(以及為什麽要這樣做)。

首先，導入所有必需的庫：

#import libraries
import pandas as pd
import numpy as np
import random as rd
import matplotlib.pyplot as plt

現在，我們將讀取CSV文件，並查看數據的前五行：

data = pd.read_csv('clustering.csv')
data.head()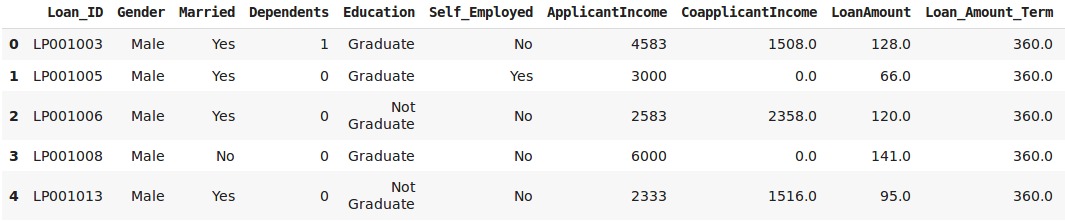

對於本文，我們僅從數據中獲取兩個變量-“LoanAmount”和“ApplicantIncome”。這樣簡化處理，數據的可視化更容易。我們選擇這兩個變量並可視化數據點：

X = data[["LoanAmount","ApplicantIncome"]]
#Visualise data points
plt.scatter(X["ApplicantIncome"],X["LoanAmount"],c='black')
plt.xlabel('AnnualIncome')
plt.ylabel('Loan Amount (In Thousands)')
plt.show()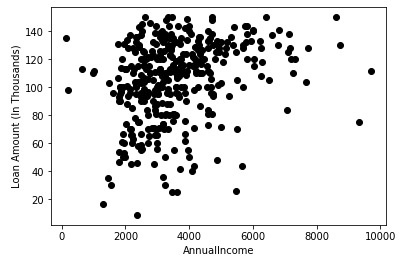

對於K-Means的步驟1和2，關於選擇簇數(k)並為每個簇選擇隨機質心——我們將選擇3個聚類，然後從數據中選擇隨機觀測值作為質心：

# Step 1 and 2 - Choose the number of clusters (k) and select random centroid for each cluster

#number of clusters
K=3

# Select random observation as centroids
Centroids = (X.sample(n=K))
plt.scatter(X[“ApplicantIncome”],X[“LoanAmount”],c=’black’)
plt.scatter(Centroids[“ApplicantIncome”],Centroids[“LoanAmount”],c=’red’)
plt.xlabel(‘AnnualIncome’)
plt.ylabel(‘Loan Amount (In Thousands)’)
plt.show()

在這裏，3個紅點分別代表3個簇質心。請注意，我們是隨機選擇這些點的，因此，每次運行此代碼時，您可能會得到不同的質心。

接下來，我們將定義一些條件來實現K-Means聚類算法。首先看一下代碼：

# Step 3 - Assign all the points to the closest cluster centroid
# Step 4 - Recompute centroids of newly formed clusters
# Step 5 - Repeat step 3 and 4

diff = 1
j=0

while(diff!=0):
    XD=X
    i=1
    for index1,row_c in Centroids.iterrows():
        ED=[]
        for index2,row_d in XD.iterrows():
            d1=(row_c["ApplicantIncome"]-row_d["ApplicantIncome"])**2
            d2=(row_c["LoanAmount"]-row_d["LoanAmount"])**2
            d=np.sqrt(d1+d2)
            ED.append(d)
        X[i]=ED
        i=i+1

    C=[]
    for index,row in X.iterrows():
        min_dist=row[1]
        pos=1
        for i in range(K):
            if row[i+1] < min_dist:
                min_dist = row[i+1]
                pos=i+1
        C.append(pos)
    X["Cluster"]=C
    Centroids_new = X.groupby(["Cluster"]).mean()[["LoanAmount","ApplicantIncome"]]
    if j == 0:
        diff=1
        j=j+1
    else:
        diff = (Centroids_new['LoanAmount'] - Centroids['LoanAmount']).sum() + (Centroids_new['ApplicantIncome'] - Centroids['ApplicantIncome']).sum()
        print(diff.sum())
    Centroids = X.groupby(["Cluster"]).mean()[["LoanAmount","ApplicantIncome"]]

注意：因為有隨機選擇質心操作，每次我們運行這些值時，結果可能跟上圖有所不同。在這裏，當質心在兩次迭代後沒有變化時，我們將停止訓練。我們最初定義了diff=1，在while循環中，我們計算前一次迭代與當前迭代中質心之間的差異作為diff。

當此差為0時，我們將停止訓練。現在，讓我們可視化結果簇：

color=['blue','green','cyan']
for k in range(K):
    data=X[X["Cluster"]==k+1]
    plt.scatter(data["ApplicantIncome"],data["LoanAmount"],c=color[k])
plt.scatter(Centroids["ApplicantIncome"],Centroids["LoanAmount"],c='red')
plt.xlabel('Income')
plt.ylabel('Loan Amount (In Thousands)')
plt.show()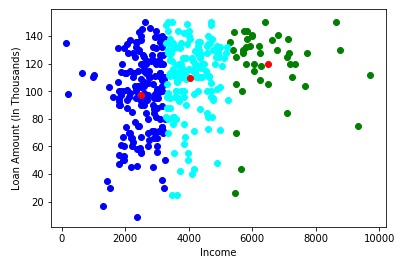

很漂亮的結果！在這裏，我們可以清晰地可視化三個群集。紅點代表每個簇的質心。希望您現在對K-Means的工作方式有清楚的了解。

但是，在某些情況下，該算法可能無法很好地執行。讓我們看看使用k-means時可能會遇到的一些挑戰。

K-Means聚類算法麵臨的挑戰

使用K-Means時，我們麵臨的常見挑戰之一是簇的大小不同。假設我們有以下幾點：

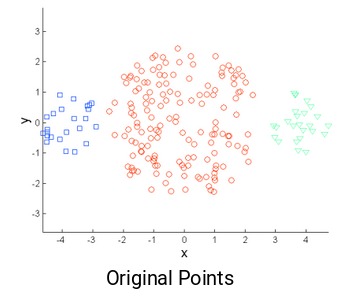
與中間的簇相比，最左側和最右側的簇較小。如果在這些點上應用k-means聚類，結果將是這樣的：

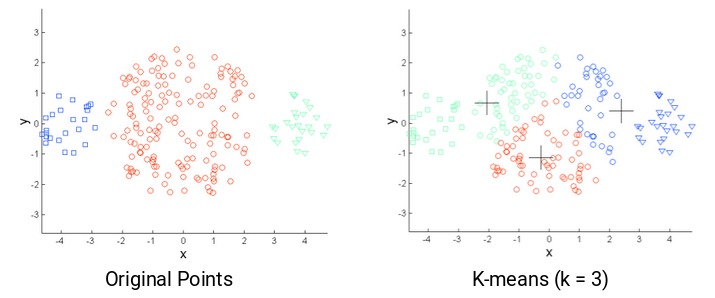
k-means的另一個挑戰是原始點的密度不同。假設這些是原始點：

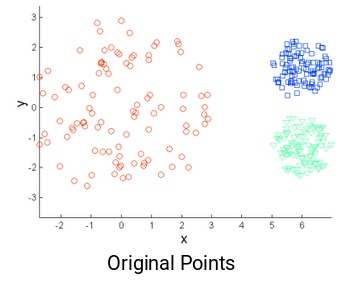
圖中，紅色簇中的點散開，而其餘簇中的點緊密堆積在一起。如果在這些點上應用k-means，我們將獲得如下所示的聚類：

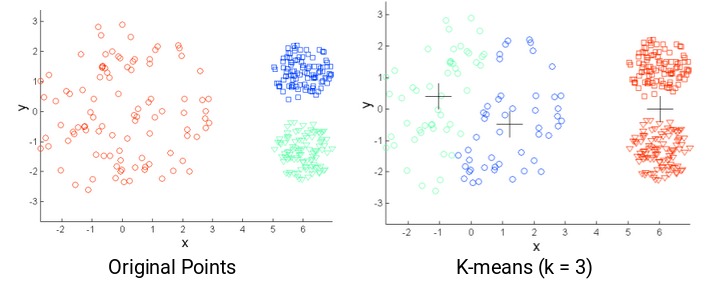
我們可以看到，2個緊促的簇已分配給單個簇。而位於同一簇中的點已分配給不同的簇。結果很不理想，該怎麽辦？

解決方案之一是使用更多數量的簇。因此，在上述幾種情況下，我們可以使用更大的簇數量，而不是使用3個簇。也許設置k = 10可能會獲得更有意義的聚類簇。

還記得我們如何在k-means聚類中隨機初始化質心嗎？嗯，這也是潛在的問題，因為我們每次都可能獲得不同的簇。因此，為了解決隨機初始化的問題，有一種算法稱為K-Means++，它可用於選擇K-Means的初始值後者說初始簇質心。

K-Means++為K-Means聚類選擇初始聚類質心

在某些情況下，如果簇的初始化不合適，則K-Means可能會得到糟糕的聚類。這是K-Means ++產生的原因，它指定了在使用標準k-means聚類算法進行操作之前初始化聚類中心的過程。

在使用K-Means ++初始化時，我們更有可能找到與理想情況最佳K-Means解決方案接近的解決方案。

使用K-Means ++初始化質心的步驟為：

1. 從我們要聚類的數據點中隨機選擇第一個聚類。這類似於我們在K-Means中所做的操作，但是我們不是在隨機選擇所有質心，而是在此處選擇一個質心
2. 接下來，我們計算每個數據點(x)與已經選擇的聚類中心的距離(D(x))
3. 然後，從數據點選擇新的聚類中心，其中點x選到作為新質心的概率與(D(x))^2成正比(即與距離的平方成正比)
4. 然後，我們重複步驟2和3，直到已選擇K個簇心

下麵舉個例子來更清楚地了解這一點。假設我們有以下幾點，我們想在這裏建立3個聚類：

第一步是隨機選擇一個數據點作為聚類質心：

假設我們選擇綠點作為初始質心。現在，我們將計算此質心到每個數據點的距離(D(x))：

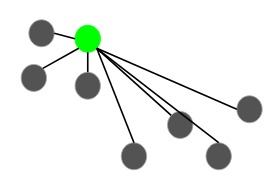
下一個質心將是其平方距離(D(x)^2)最大即離當前質心最遠的那個：

也就是說，紅點將被選作下一個質心。然後，要選擇最後一個質心，我們計算每個點與其最近的質心的距離，並選擇平方距最大的點作為下一個質心：

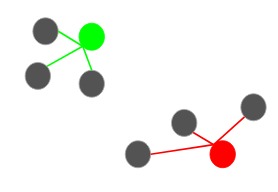
我們將最後一個質心選擇為藍色點：

初始化質心後，使用標準K-Means算法即可。使用K-Means ++初始化質心會改善聚類效果。雖然相對於隨機初始化，它的計算成本很高，但隨後的K-Means收斂速度通常更快。

接下來的問題是-我們應該聚類為幾個簇？也就是說，執行K-Means時，簇的最佳數目應該是多少？

如何為K-Means聚類選擇正確的簇數量？

使用K-Means時，最普遍的疑問之一就是如何選擇正確的簇數量。

這裏介紹一種技術，該技術幫助我們為K-Means算法選擇正確的簇值。還是以前麵看到的客戶細分為例。回顧一下，該銀行希望根據客戶的收入和債務金額對其客戶進行細分：

在這裏，我們可以用2聚類將客戶分開，如下所示：

所有低收入客戶都在一個簇中，而高收入客戶都在第二個簇中。我們還可以有4個聚類：

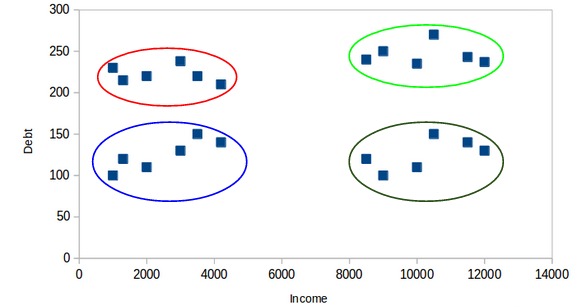
在這裏，一個簇可能代表低收入和低負債的客戶，另一個簇可能是那些高收入，高負債的客戶，依此類推。當然，也可以有8個簇：

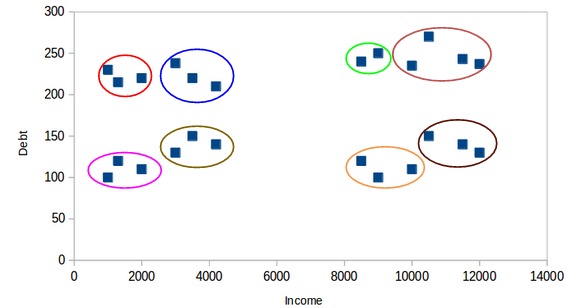
實際上，我們可以有任意數量的簇。最極端的情況，可以把每個點分配給一個單獨的簇。在這種情況下，聚類簇的數量將等於觀測點的數量。所以，

聚類的最大可能數目將等於數據集中的觀測點數目。

但是，我們如何才能確定最佳的簇數呢？我們可以做的是繪製一個圖，也稱為彎頭曲線，其中x軸將代表簇的數量，而y軸為評估指標(比如說：慣性)。

當然，您還可以選擇任何其他評估指標，例如鄧恩指數(Dunn Index)：

接下來，我們將從一個小的簇數開始，比如說2。使用2個簇訓練模型，計算該模型的慣性，最後將其繪製在上圖中。假設我們的慣性值約為1000：

現在，我們將增加簇的數量，再次訓練模型，並繪製慣性值。得到的曲線圖如下：

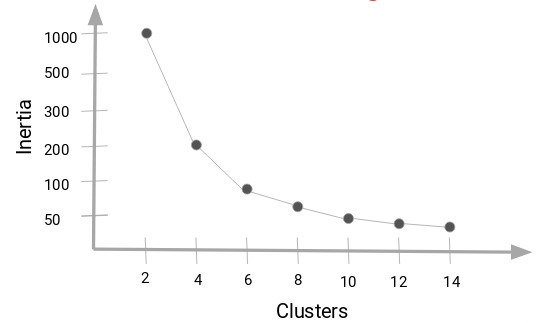
當我們將簇值從2更改為4時，慣性值會急劇下降。隨著我們進一步增加簇的數量，慣性值將減小並最終變為恒定值。所以，

可以將慣性值的減小變為恒定的聚類值作為我們數據的正確聚類值。

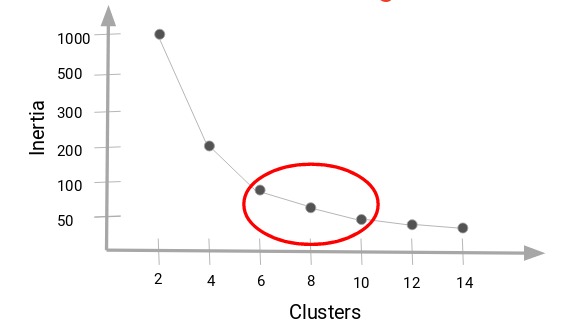
在這裏，我們可以選擇6到10之間的任意值作為簇數。在確定聚類簇數時，還必須考慮計算成本。如果我們增加聚類的數量，計算成本也會增加。因此，如果您沒有大量的計算資源，我的建議是選擇數量較少的簇數。

接下來，我們在Python使用算法庫實現真正的K-Means聚類算法。我們還將看到如何使用K-Means++初始化質心，並且繪製出彎頭曲線以決定數據集上合適的聚類數量。

在Python中實現K-Means集群[算法庫庫版】

我們將致力於解決批發客戶細分問題。您可以使用這個連結下載數據集。數據托管在UCI機器學習存儲庫中。

此問題的目的是根據批發分銷商的客戶每年在各種產品類別(如牛奶，雜貨，地區等)上的支出進行細分。接下來，看代碼吧！

首先導入所需的庫：

# importing required libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.cluster import KMeans

接下來，加載數據並查看前五行：

# reading the data and looking at the first five rows of the data
data=pd.read_csv("Wholesale customers data.csv")
data.head()

我們擁有客戶在牛奶，雜貨，冷凍，洗滌劑等不同產品上的支出明細。然後，我們必須根據提供的明細對客戶進行細分。在此之前，我們先提取一些與數據有關的統計信息：

# statistics of the data                       
data.describe()

在這裏，我們看到數據大小存在很多變化。渠道和區域等變量的幅度較小，而鮮食，牛奶，雜貨等變量的幅度較高。

由於K-Means是基於距離的算法，因此，這種幅度上的差異會產生問題。因此，首先標準化變量達到相同的尺度：

# standardizing the data
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
data_scaled = scaler.fit_transform(data)

# statistics of scaled data
pd.DataFrame(data_scaled).describe()

現在的大小看起來相似。接下來，讓我們創建一個kmeans模型並將其擬合到數據上：

# defining the kmeans function with initialization as k-means++
kmeans = KMeans(n_clusters=2, init='k-means++')

# fitting the k means algorithm on scaled data
kmeans.fit(data_scaled)

我們初始化了兩個簇。注意：初始化在這裏不是隨機的，我們使用了k-means ++初始化，這通常會產生更好的結果，正如我們在上一節中所討論的那樣。

接下來評估形成的簇效果。為此，我們將計算聚類的慣性：

# inertia on the fitted data
kmeans.inertia_

輸出：2599.38555935614

我們得到的慣性值幾乎為2600。現在，讓我們看看如何使用彎頭曲線來確定最佳簇數。

首先擬合多個k-means模型: 每個聚類模型使用不同的簇數量，簇數量依次增加。計算每個模型的慣性值，然後將其繪製以可視化結果：

# fitting multiple k-means algorithms and storing the values in an empty list
SSE = []
for cluster in range(1,20):
    kmeans = KMeans(n_jobs = -1, n_clusters = cluster, init='k-means++')
    kmeans.fit(data_scaled)
    SSE.append(kmeans.inertia_)

# converting the results into a dataframe and plotting them
frame = pd.DataFrame({‘Cluster’:range(1,20), ‘SSE’:SSE})
plt.figure(figsize=(12,6))
plt.plot(frame[‘Cluster’], frame[‘SSE’], marker=’o’)
plt.xlabel(‘Number of clusters’)
plt.ylabel(‘Inertia’)

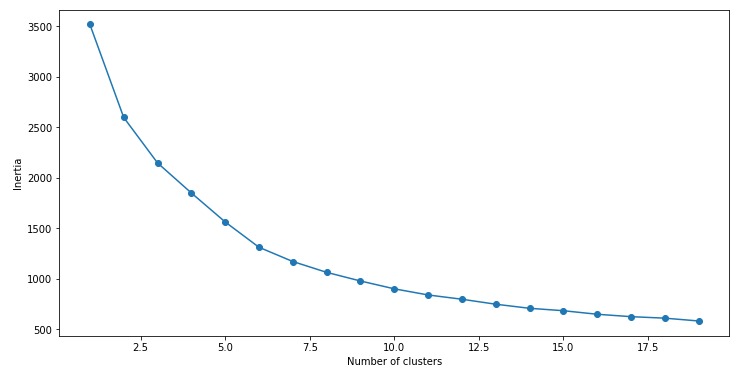
您能從該圖中得知最佳聚類值嗎？看上麵的肘彎，我們可以選擇5到8之間的任意數量的聚類簇值。比如我們將簇數設置為6並擬合模型：

# k means using 5 clusters and k-means++ initialization
kmeans = KMeans(n_jobs = -1, n_clusters = 5, init='k-means++')
kmeans.fit(data_scaled)
pred = kmeans.predict(data_scaled)

最後，讓我們看一下每個上述聚類中的點數計數：

frame = pd.DataFrame(data_scaled)
frame['cluster'] = pred
frame['cluster'].value_counts()

可以看到，屬於聚類4的有234個數據點(索引3)，然後屬於聚類2的有125個數據點(索引1)，依此類推。

以上就是我們如何在Python中實現K-Means聚類的方法。

尾注

在本文中，我們討論了最著名的聚類算法之一——K-Means。我們從頭開始實現Kmens算法，並研究了一步一步如何實現。另外，也探討了使用K-Means時可能麵臨的挑戰，並介紹了K-Means ++在初始化聚類質心時如何提供幫助。

最後，我們實現了Python版本的k-means，並繪製了彎頭曲線，該曲線有助於在K-Means算法中找到最佳的簇數。