保序回归简介
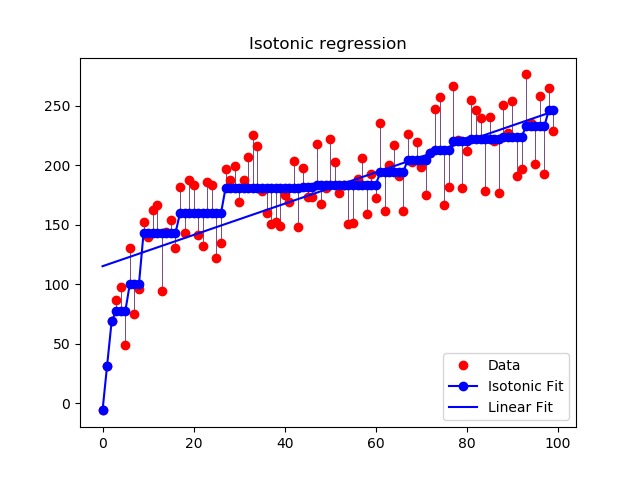
本示例是对保序回归处理生成数据的说明。保序回归发现函数的非递减近似,同时使训练数据的均方误差最小。这种模型的好处是它不会为目标函数采用任何形式的假设,例如线性。为了比较,示例中还给出了线性回归。
代码实现[Python]
# -*- coding: utf-8 -*-
print(__doc__)
# 码农: Nelle Varoquaux
# Alexandre Gramfort
# 协议: BSD
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection
from sklearn.linear_model import LinearRegression
from sklearn.isotonic import IsotonicRegression
from sklearn.utils import check_random_state
n = 100
x = np.arange(n)
rs = check_random_state(0)
y = rs.randint(-50, 50, size=(n,)) + 50. * np.log1p(np.arange(n))
# #############################################################################
# 拟合IsotonicRegression和LinearRegression models模型
ir = IsotonicRegression()
y_ = ir.fit_transform(x, y)
lr = LinearRegression()
lr.fit(x[:, np.newaxis], y) # x needs to be 2d for LinearRegression
# #############################################################################
# 绘图展示结果
segments = [[[i, y[i]], [i, y_[i]]] for i in range(n)]
lc = LineCollection(segments, zorder=0)
lc.set_array(np.ones(len(y)))
lc.set_linewidths(np.full(n, 0.5))
fig = plt.figure()
plt.plot(x, y, 'r.', markersize=12)
plt.plot(x, y_, 'b.-', markersize=12)
plt.plot(x, lr.predict(x[:, np.newaxis]), 'b-')
plt.gca().add_collection(lc)
plt.legend(('Data', 'Isotonic Fit', 'Linear Fit'), loc='lower right')
plt.title('Isotonic regression')
plt.show()
代码执行
代码运行时间大约:0分0.056秒。
运行代码输出的图片内容如下:
源码下载
- Python版源码文件: plot_isotonic_regression.py
- Jupyter Notebook版源码文件: plot_isotonic_regression.ipynb
