自动编码器概览

如下图所示[自动编码器=>AutoEncoder]：

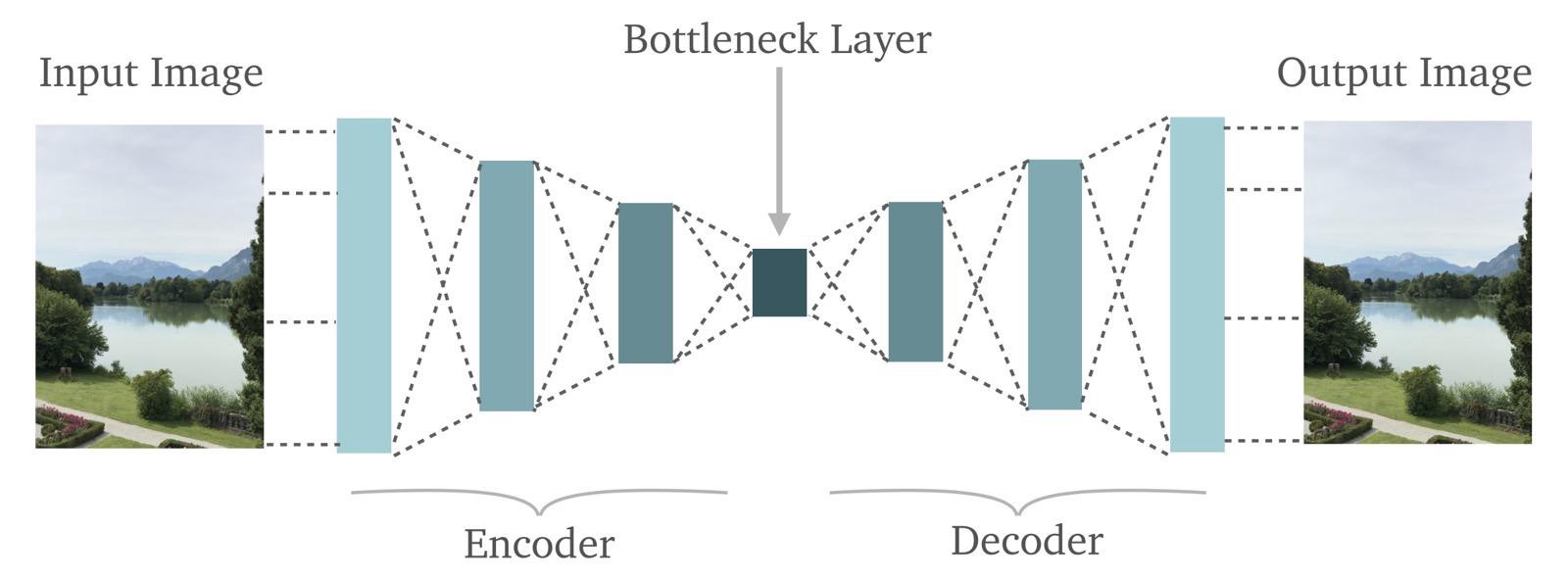
有关上图的几点：

自动编码器正是我们所说的那样：它在输出端重建了输入。即它通过：首先“编码”输入图像，然后将“编码”图像“解码”为原始图像来实现。
在图中间，我们标记了一个“瓶颈”层(Bottleneck Layer)。从这个“瓶颈”可以看到，自动编码器可以作为非常强大的信息压缩工具。

让我们从左到右细看每一层

输入图片：很明显，这我们想要重建的图像。这是一个RBG图像，这意味着它有三个维度。高度，宽度和颜色深度。
编码器：编码器只不过是神经网络(一种深度神经网络或者卷积神经网络，但因为它是一个图像，我们最好假设它是后者)。基本上，编码器接收输入并将其转换为较小的密集表示，解码器网络可以使用该表示将其转换回原始输入。
瓶颈层：瓶颈层只不过是编码器网络的最后一层。这是对图像信息的“较小，密集的表现形式”所在的地方。
解码器：解码器网络与编码器网络完全相反。编码器网络获取输入图像并将其转换为更压缩的表示。然后，解码器网络从瓶颈层获取该压缩表示并尝试重建原始图像。

揭开编码器的神秘面纱

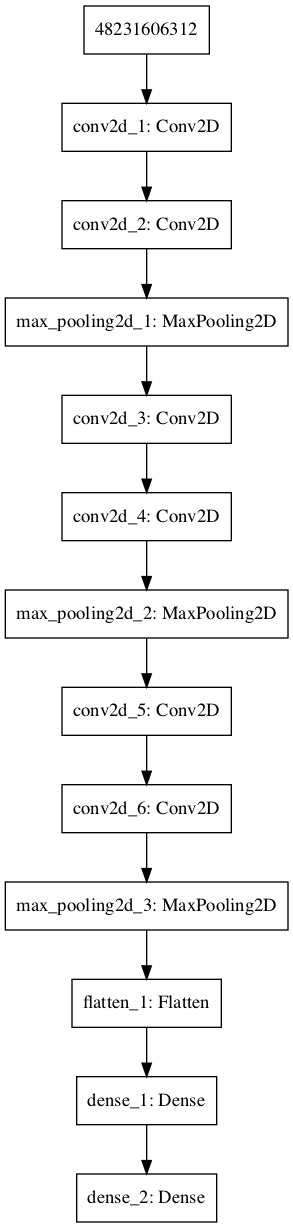
回想一下卷积神经网络的内容，例如我们将MNIST Fashion数据集分类。模型架构如下图，我们还给出了模型架构的汇总信息，其中包括层的类型、大小及其输出形状。

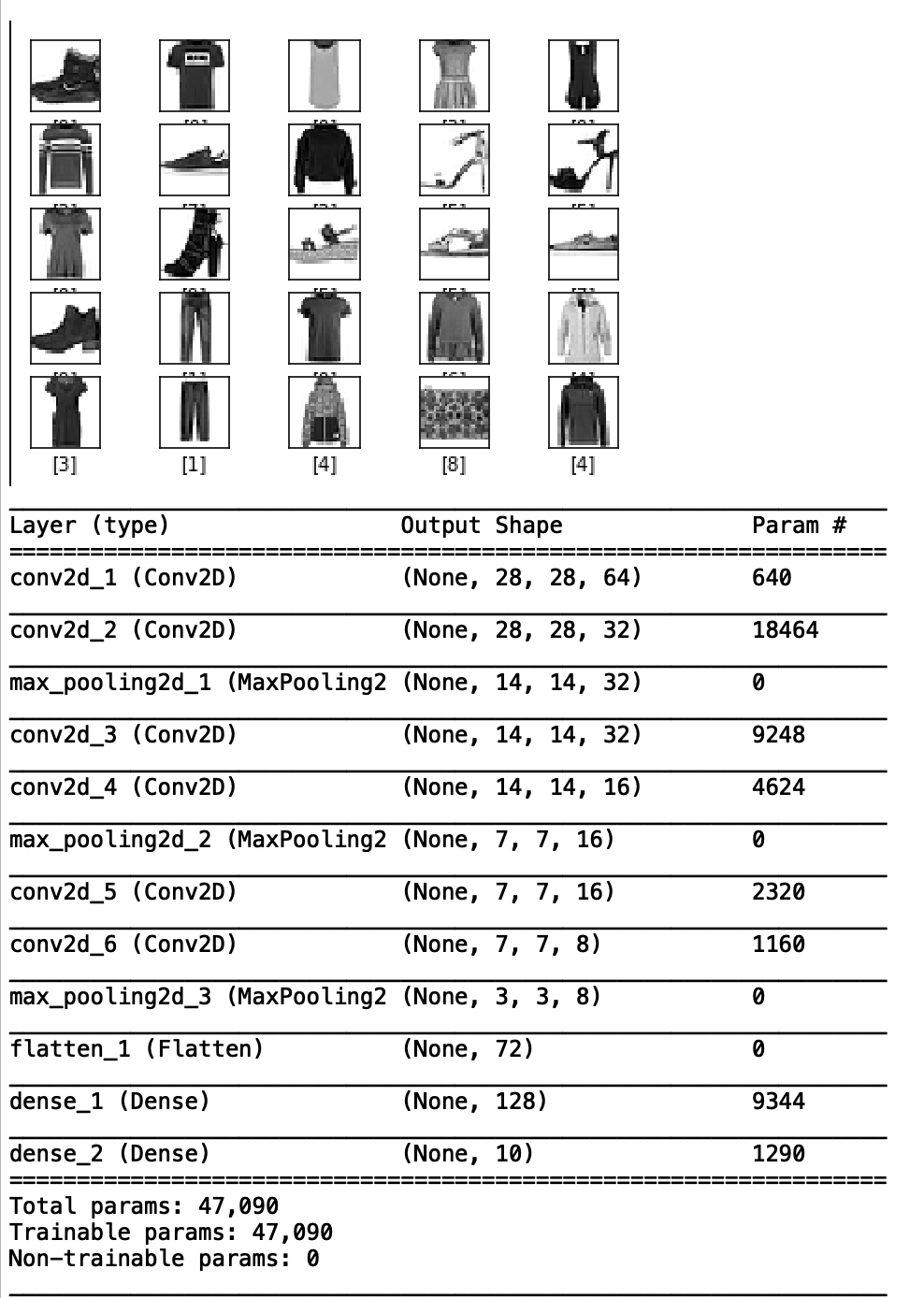
模型结构和输出形状的说明：

MNIST Fashion数据中的每张图片大小为28×28。我们的第一层是一个带有64个滤波器的卷积层。因此，第一层的输出为28x28x64。
类似地，第二层的输出是28x28x32，因为第二层是带有32个滤波器的卷积。
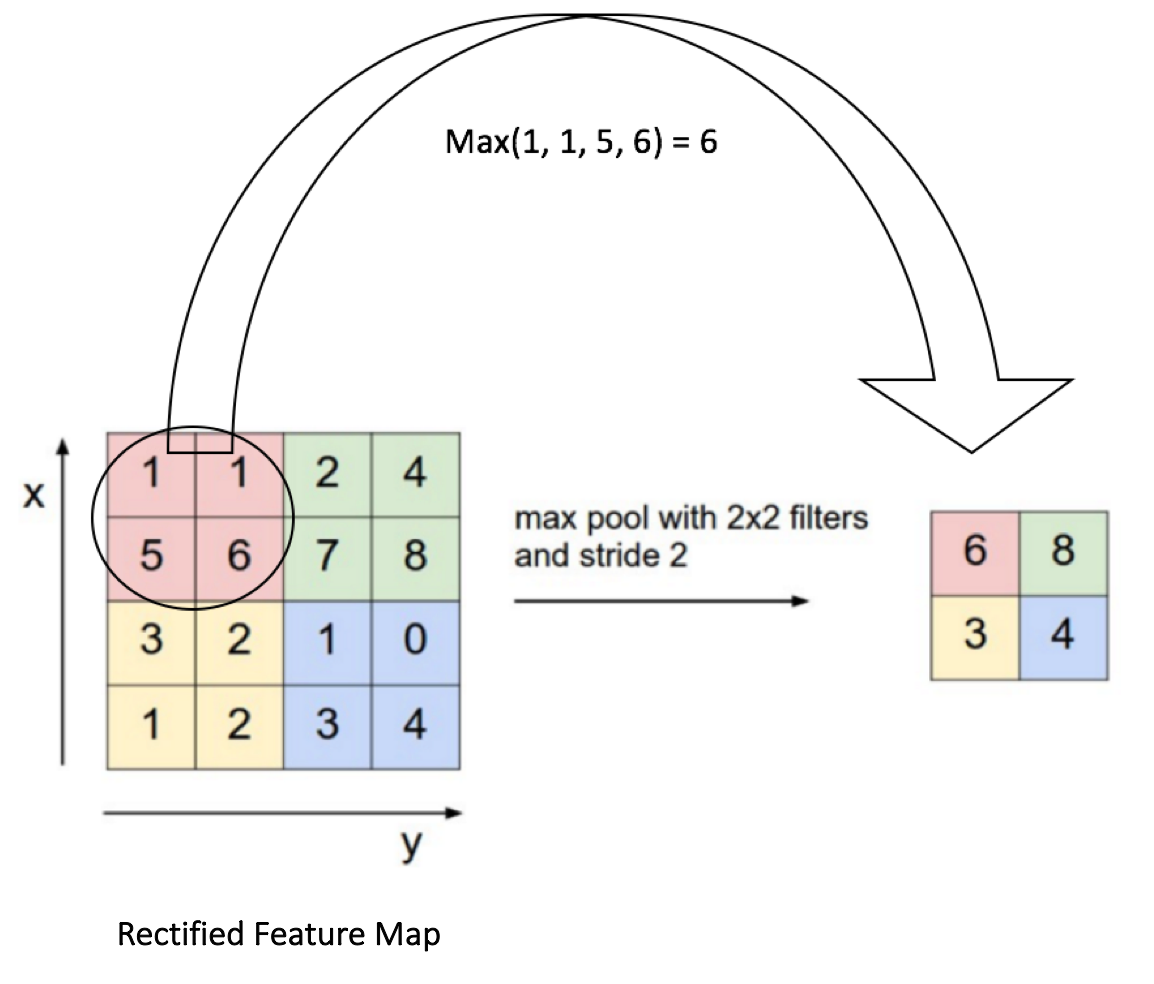
但现在考虑模型流程图中的第三层以及模型摘要。我们使用的第三层是Max Pooling Layer。这一层的功能是通过在特征图中取最大的激活来逐步减小表示的空间大小。我们在下面提供了一张图片供参考。注意图的大小从4×4到2×2。现在再次查看我们的模型摘要，可以很容易地将第三个Max Pooling图层的输出关联为14x14x32。及之前图的一半尺寸。

如何编程实现一个自动编码器？

第1步：加载数据

我们将要使用的数据是常用的MNIST手写数字数据集：

60,000张训练图像和10,000张测试图像。

数据集中的每个手写数字都是标准化的28×28灰度图像。示例如下：

加载数据很容易，因为Keras已经在其API中提供了数据集。我们使用以下行来调用它：

from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()

OUTPUT：

使用TensorFlow后端。

从中下载数据

11493376/11490434 [==============================] – 4s 0us /step

我们的目标是使用自动编码器重建这些数字。

但我们不只是重建数据集中的数字。我们实际上会通过向其添加随机噪声来破坏数字，然后我们将恢复原始数字。

这中做法叫做去燥自动编码器。

第2步：自动编码器Coding

import numpy as np
import matplotlib.pyplot as plt
from keras.datasets import mnist
from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D
from keras.models import Model
from keras import backend as K
//Load Dataset
(x_train, _), (x_test, _) = mnist.load_data()
//Scale Dataset values to lie between 0 and 1
x_train = x_train.astype(‘float32’) / 255.
x_test = x_test.astype(‘float32’) / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))
//Add Noise to our MNNIST Dataset by sampling random values from Gaussian distribution by using np.random.normal() and adding it to our original images to change pixel values
noise_factor = 0.5
x_train_noisy = x_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_train.shape)
x_test_noisy = x_test + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_test.shape)
x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)
//Visualising the Noisy Digits using Matplotlib
n = 10 //change this number to visualise more digits.
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i)
plt.imshow(x_test_noisy[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

OUTPUT：

所以现在我们有了嘈杂的数字。现在要恢复原始数字。

我们将使用卷积自动编码器，它将卷积神经网络 作为编码器和解码器。

//Specify the Input Layer size which is 28x28x1
input_img = Input(shape=(28, 28, 1))

这里用到了MaxPooling2D层。而UpSampling2D层与MaxPooling2D完全相反。如果MaxPooling2D缩小输入大小，UpSampling2D会将其变大。

这很直观，为什么我们可能需要扩大图像。在编码器将输入减少到瓶颈层的压缩表示之后，解码器需要扩展该压缩表示，因为复原的图像需要返回相同的原始尺寸。

//Model Construction
x = Conv2D(32, (3, 3), activation=’relu’, padding=’same’)(input_img)
x = MaxPooling2D((2, 2), padding=’same’)(x)
x = Conv2D(32, (3, 3), activation=’relu’, padding=’same’)(x)
encoded = MaxPooling2D((2, 2), padding=’same’)(x)
//At this point the representation is (7, 7, 32)
x = Conv2D(32, (3, 3), activation=’relu’, padding=’same’)(encoded)
x = UpSampling2D((2, 2))(x)
x = Conv2D(32, (3, 3), activation=’relu’, padding=’same’)(x)
x = UpSampling2D((2, 2))(x)
decoded = Conv2D(1, (3, 3), activation=’sigmoid’, padding=’same’)(x)
autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer=’adam’, loss=’binary_crossentropy’)

由于输入图像和重建图像都是灰度的，我们使用二元cross-entropy作为损失函数，因为值将介于0和1之间。

如果我们使用彩色图像，我们无法用二元cross-entropy获得很好的结果，因为现在目标的值(在自动编码器的情况下输入图像)不会介于0和1之间，而是介于0到255之间。

因此，您要么使用像均值平方误差(MSE)这样的损失函数，要么预处理图像素值到0到1之间。

一旦我们编译了模型，我们就可以使用.fit()方法来训练网络。训练100轮次，我们将使用x_train作为我们的标签而不是x_train_noisy，正如您对自动编码器所期望的那样，因为现在我们不再对输入重建感兴趣，我们对恢复原始输入感兴趣。

aautoencoder.fit(x_train_noisy, x_train,
epochs=100,
batch_size=128,
shuffle=True,
validation_data=(x_test_noisy, x_test),
)

在模型训练100个轮次，我们可以检查我们的模型是否真的能够消除噪音。

如下图所示，我们训练有素的卷积自动编码器已经学会了如何对图像进行去噪！事实上，尽管我们投入了很多噪音，但它在恢复原始图像方面做得非常出色！

参考资料

Autoencoders in Keras