自動編碼器概覽

如下圖所示[自動編碼器=>AutoEncoder]：

有關上圖的幾點：

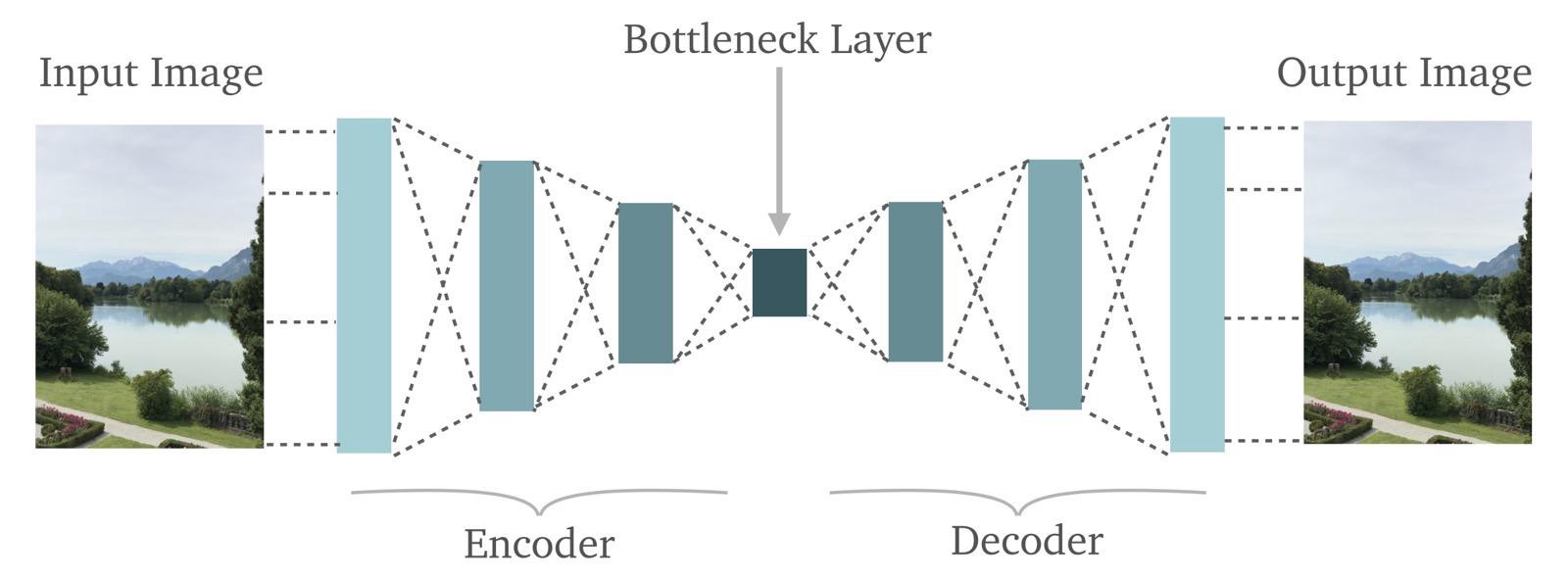
自動編碼器正是我們所說的那樣：它在輸出端重建了輸入。即它通過：首先“編碼”輸入圖像，然後將“編碼”圖像“解碼”為原始圖像來實現。
在圖中間，我們標記了一個“瓶頸”層(Bottleneck Layer)。從這個“瓶頸”可以看到，自動編碼器可以作為非常強大的信息壓縮工具。

讓我們從左到右細看每一層

輸入圖片：很明顯，這我們想要重建的圖像。這是一個RBG圖像，這意味著它有三個維度。高度，寬度和顏色深度。
編碼器：編碼器隻不過是神經網絡(一種深度神經網絡或者卷積神經網絡，但因為它是一個圖像，我們最好假設它是後者)。基本上，編碼器接收輸入並將其轉換為較小的密集表示，解碼器網絡可以使用該表示將其轉換回原始輸入。
瓶頸層：瓶頸層隻不過是編碼器網絡的最後一層。這是對圖像信息的“較小，密集的表現形式”所在的地方。
解碼器：解碼器網絡與編碼器網絡完全相反。編碼器網絡獲取輸入圖像並將其轉換為更壓縮的表示。然後，解碼器網絡從瓶頸層獲取該壓縮表示並嘗試重建原始圖像。

揭開編碼器的神秘麵紗

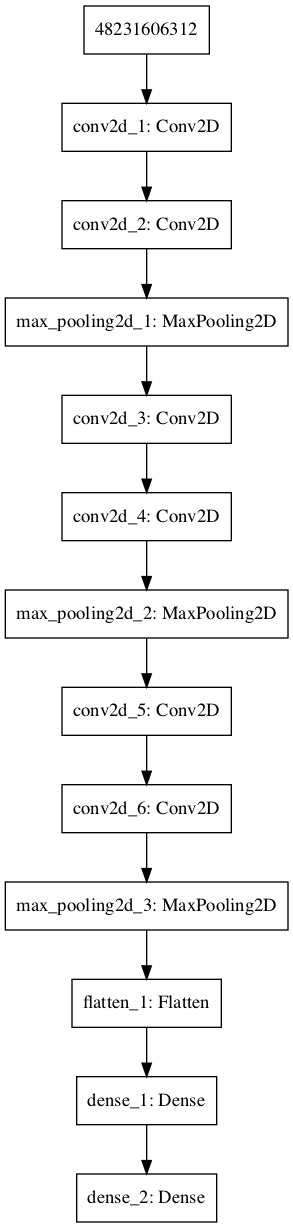
回想一下卷積神經網絡的內容，例如我們將MNIST Fashion數據集分類。模型架構如下圖，我們還給出了模型架構的匯總信息，其中包括層的類型、大小及其輸出形狀。

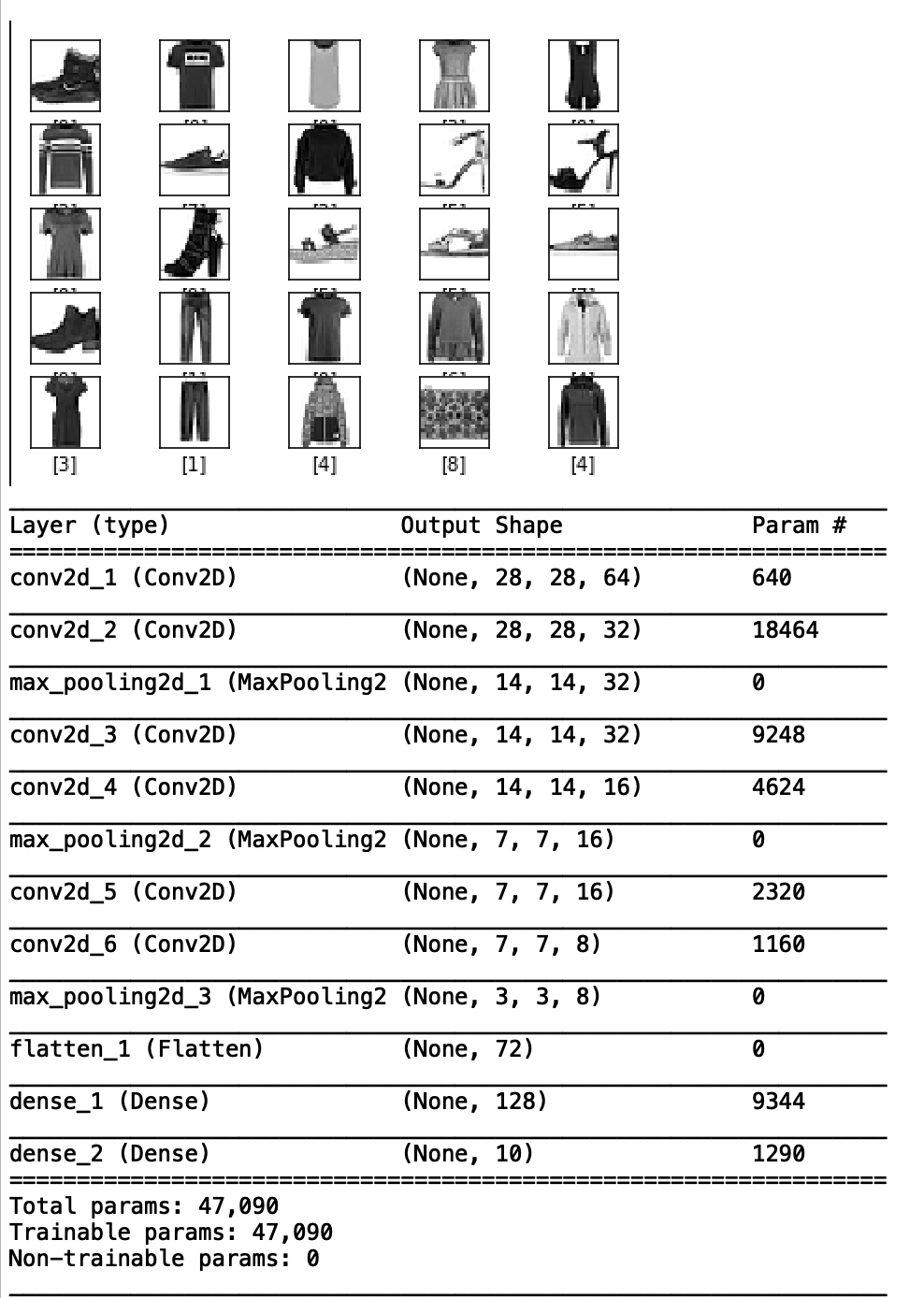
模型結構和輸出形狀的說明：

MNIST Fashion數據中的每張圖片大小為28×28。我們的第一層是一個帶有64個濾波器的卷積層。因此，第一層的輸出為28x28x64。
類似地，第二層的輸出是28x28x32，因為第二層是帶有32個濾波器的卷積。
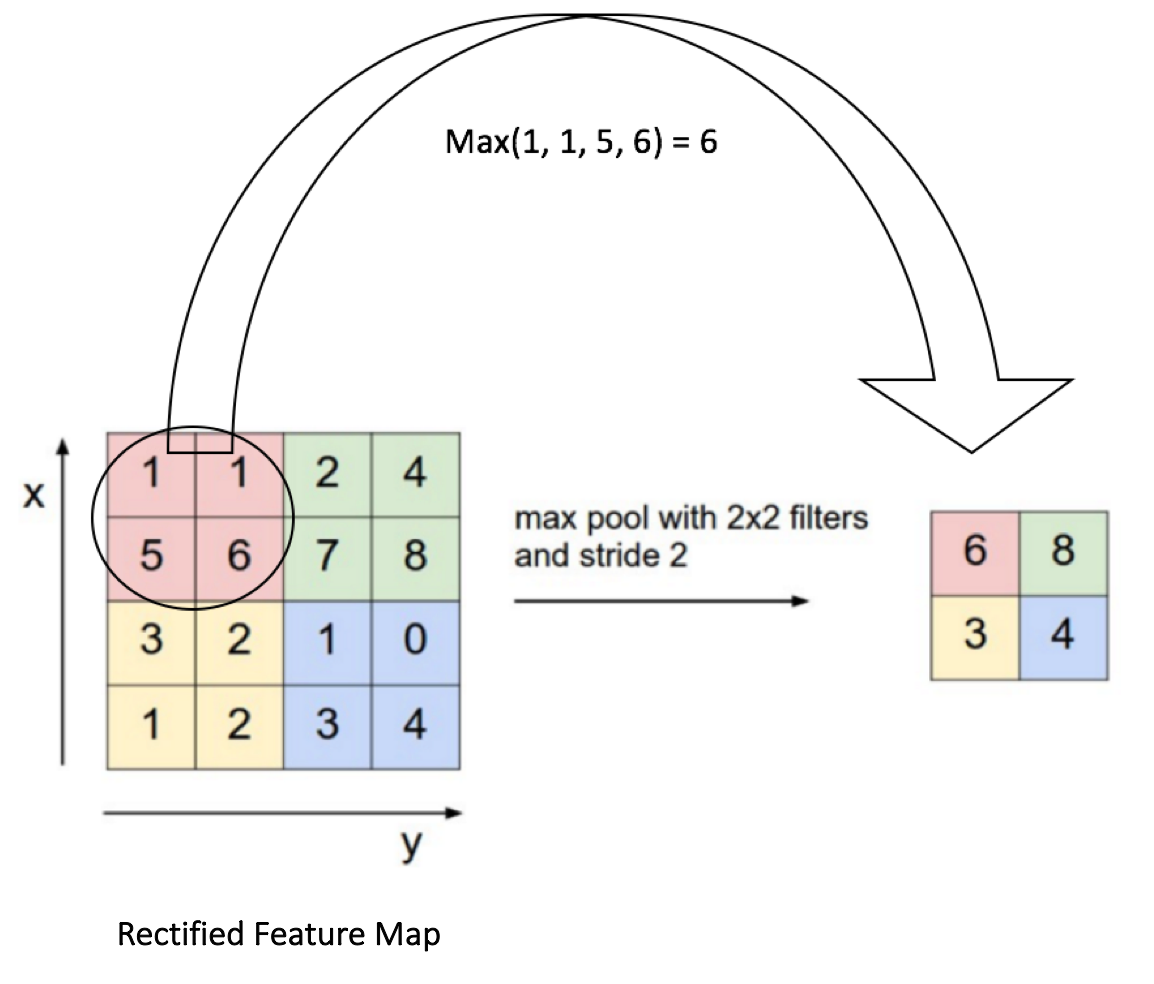
但現在考慮模型流程圖中的第三層以及模型摘要。我們使用的第三層是Max Pooling Layer。這一層的功能是通過在特征圖中取最大的激活來逐步減小表示的空間大小。我們在下麵提供了一張圖片供參考。注意圖的大小從4×4到2×2。現在再次查看我們的模型摘要，可以很容易地將第三個Max Pooling圖層的輸出關聯為14x14x32。及之前圖的一半尺寸。

如何編程實現一個自動編碼器？

第1步：加載數據

我們將要使用的數據是常用的MNIST手寫數字數據集：

60,000張訓練圖像和10,000張測試圖像。

數據集中的每個手寫數字都是標準化的28×28灰度圖像。示例如下：

加載數據很容易，因為Keras已經在其API中提供了數據集。我們使用以下行來調用它：

from keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()

OUTPUT：

使用TensorFlow後端。

從中下載數據

11493376/11490434 [==============================] – 4s 0us /step

我們的目標是使用自動編碼器重建這些數字。

但我們不隻是重建數據集中的數字。我們實際上會通過向其添加隨機噪聲來破壞數字，然後我們將恢複原始數字。

這中做法叫做去燥自動編碼器。

第2步：自動編碼器Coding

import numpy as np
import matplotlib.pyplot as plt
from keras.datasets import mnist
from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D
from keras.models import Model
from keras import backend as K
//Load Dataset
(x_train, _), (x_test, _) = mnist.load_data()
//Scale Dataset values to lie between 0 and 1
x_train = x_train.astype(‘float32’) / 255.
x_test = x_test.astype(‘float32’) / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))
//Add Noise to our MNNIST Dataset by sampling random values from Gaussian distribution by using np.random.normal() and adding it to our original images to change pixel values
noise_factor = 0.5
x_train_noisy = x_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_train.shape)
x_test_noisy = x_test + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_test.shape)
x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)
//Visualising the Noisy Digits using Matplotlib
n = 10 //change this number to visualise more digits.
plt.figure(figsize=(20, 2))
for i in range(n):
ax = plt.subplot(1, n, i)
plt.imshow(x_test_noisy[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

OUTPUT：

所以現在我們有了嘈雜的數字。現在要恢複原始數字。

我們將使用卷積自動編碼器，它將卷積神經網絡 作為編碼器和解碼器。

//Specify the Input Layer size which is 28x28x1
input_img = Input(shape=(28, 28, 1))

這裏用到了MaxPooling2D層。而UpSampling2D層與MaxPooling2D完全相反。如果MaxPooling2D縮小輸入大小，UpSampling2D會將其變大。

這很直觀，為什麽我們可能需要擴大圖像。在編碼器將輸入減少到瓶頸層的壓縮表示之後，解碼器需要擴展該壓縮表示，因為複原的圖像需要返回相同的原始尺寸。

//Model Construction
x = Conv2D(32, (3, 3), activation=’relu’, padding=’same’)(input_img)
x = MaxPooling2D((2, 2), padding=’same’)(x)
x = Conv2D(32, (3, 3), activation=’relu’, padding=’same’)(x)
encoded = MaxPooling2D((2, 2), padding=’same’)(x)
//At this point the representation is (7, 7, 32)
x = Conv2D(32, (3, 3), activation=’relu’, padding=’same’)(encoded)
x = UpSampling2D((2, 2))(x)
x = Conv2D(32, (3, 3), activation=’relu’, padding=’same’)(x)
x = UpSampling2D((2, 2))(x)
decoded = Conv2D(1, (3, 3), activation=’sigmoid’, padding=’same’)(x)
autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer=’adam’, loss=’binary_crossentropy’)

由於輸入圖像和重建圖像都是灰度的，我們使用二元cross-entropy作為損失函數，因為值將介於0和1之間。

如果我們使用彩色圖像，我們無法用二元cross-entropy獲得很好的結果，因為現在目標的值(在自動編碼器的情況下輸入圖像)不會介於0和1之間，而是介於0到255之間。

因此，您要麽使用像均值平方誤差(MSE)這樣的損失函數，要麽預處理圖像素值到0到1之間。

一旦我們編譯了模型，我們就可以使用.fit()方法來訓練網絡。訓練100輪次，我們將使用x_train作為我們的標簽而不是x_train_noisy，正如您對自動編碼器所期望的那樣，因為現在我們不再對輸入重建感興趣，我們對恢複原始輸入感興趣。

aautoencoder.fit(x_train_noisy, x_train,
epochs=100,
batch_size=128,
shuffle=True,
validation_data=(x_test_noisy, x_test),
)

在模型訓練100個輪次，我們可以檢查我們的模型是否真的能夠消除噪音。

如下圖所示，我們訓練有素的卷積自動編碼器已經學會了如何對圖像進行去噪！事實上，盡管我們投入了很多噪音，但它在恢複原始圖像方麵做得非常出色！

參考資料

Autoencoders in Keras