Python Scipy stats.kurtosis()用法及代碼示例

scipy.stats.kurtosis(array, axis=0, fisher=True, bias=True)函數計算數據集的峰度(Fisher或Pearson)。它是第四個中心矩除以方差的平方。它是“tailedness”的量度，即real-valued隨機變量的概率分布形狀的描述符。簡而言之，這可以說是衡量粗尾與正態分布相比的一種方法。

其公式-

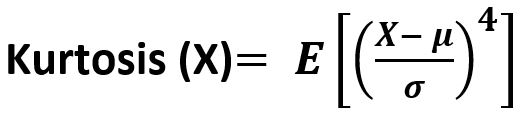
參數：
array : 具有元素的輸入數組或對象。
axis : 將測量峰度值的軸。默認情況下，軸= 0。
fisher : 布爾如果為True，則使用Fisher定義(正常為0.0)；否則，如果設置為False，則使用Pearson的定義(標準3.0)。
bias : 布爾如果設置為False，則針對統計偏差對計算進行校正。

返回值：數據集的正態分布的峰度值。

代碼1：

# Graph using numpy.linspace()  
# finding kurtosis 
  
from scipy.stats import kurtosis 
import numpy as np  
import pylab as p  
  
x1 = np.linspace( -5, 5, 1000 ) 
y1 = 1./(np.sqrt(2.*np.pi)) * np.exp( -.5*(x1)**2  ) 
  
p.plot(x1, y1, '*') 
  
  
print( '\nKurtosis for normal distribution :', kurtosis(y1)) 
  
print( '\nKurtosis for normal distribution :',  
      kurtosis(y1, fisher = False)) 
  
print( '\nKurtosis for normal distribution :',  
      kurtosis(y1, fisher = True))

輸出：



Kurtosis for normal distribution : -0.3073930877422071

Kurtosis for normal distribution : 2.692606912257793

Kurtosis for normal distribution : -0.3073930877422071

相關用法

注：本文由純淨天空篩選整理自vishal3096大神的英文原創作品 scipy stats.kurtosis() function | Python。非經特殊聲明，原始代碼版權歸原作者所有，本譯文未經允許或授權，請勿轉載或複製。