本文簡要介紹 python 語言中 scipy.stats.qmc.geometric_discrepancy 的用法。
用法:
scipy.stats.qmc.geometric_discrepancy(sample, method='mindist', metric='euclidean')#給定樣本基於其幾何特性的差異。
- sample: 數組 (n, d)
計算差異的樣本。
- method: {“mindist”, “mst”},可選
使用的方法。
mindist之一用於最小距離(默認)或mst用於最小生成樹。- metric: str 或可調用,可選
要使用的距離度量。有關可用指標和默認值,請參閱
scipy.spatial.distance.pdist的文檔。
- discrepancy: 浮點數
差異(較高的值對應於較高的樣本均勻性)。
參數 ::
返回 ::
注意:
這種差異可以作為隨機樣本質量的簡單衡量標準。該度量基於樣本中點分布的幾何特性,例如任何點對之間的最小距離,或最小生成樹中的平均邊長度。
值越高,參數空間的覆蓋性越好。請注意,這與
scipy.stats.qmc.discrepancy不同,其中較低的值對應於較高的樣本質量。另請注意,使用此函數比較不同的采樣策略時,樣本大小必須保持不變。
可以從最小生成樹計算兩個度量:平均邊長度和邊長度的標準偏差。與單獨使用任一指標相比,使用這兩個指標可以更好地說明均勻性,並且優選較高的均值和較低的標準差(請參閱 [1] 進行簡要討論)。該函數目前僅計算平均邊長。
參考:
[1]弗蘭科·J.等人。 “最小生成樹:評估計算機實驗設計質量的新方法。”化學計量學和智能實驗室係統,97 (2),第 164-169 頁,2009 年。
例子:
使用最小歐氏距離(默認值)計算樣本的質量:
>>> import numpy as np >>> from scipy.stats import qmc >>> rng = np.random.default_rng() >>> sample = qmc.LatinHypercube(d=2, seed=rng).random(50) >>> qmc.geometric_discrepancy(sample) 0.03708161435687876使用最小生成樹中的平均邊長計算質量:
>>> qmc.geometric_discrepancy(sample, method='mst') 0.1105149978798376顯示最小生成樹和距離最小的點:
>>> import matplotlib.pyplot as plt >>> from matplotlib.lines import Line2D >>> from scipy.sparse.csgraph import minimum_spanning_tree >>> from scipy.spatial.distance import pdist, squareform >>> dist = pdist(sample) >>> mst = minimum_spanning_tree(squareform(dist)) >>> edges = np.where(mst.toarray() > 0) >>> edges = np.asarray(edges).T >>> min_dist = np.min(dist) >>> min_idx = np.argwhere(squareform(dist) == min_dist)[0] >>> fig, ax = plt.subplots(figsize=(10, 5)) >>> _ = ax.set(aspect='equal', xlabel=r'$x_1$', ylabel=r'$x_2$', ... xlim=[0, 1], ylim=[0, 1]) >>> for edge in edges: ... ax.plot(sample[edge, 0], sample[edge, 1], c='k') >>> ax.scatter(sample[:, 0], sample[:, 1]) >>> ax.add_patch(plt.Circle(sample[min_idx[0]], min_dist, color='red', fill=False)) >>> markers = [ ... Line2D([0], [0], marker='o', lw=0, label='Sample points'), ... Line2D([0], [0], color='k', label='Minimum spanning tree'), ... Line2D([0], [0], marker='o', lw=0, markerfacecolor='w', markeredgecolor='r', ... label='Minimum point-to-point distance'), ... ] >>> ax.legend(handles=markers, loc='center left', bbox_to_anchor=(1, 0.5)); >>> plt.show()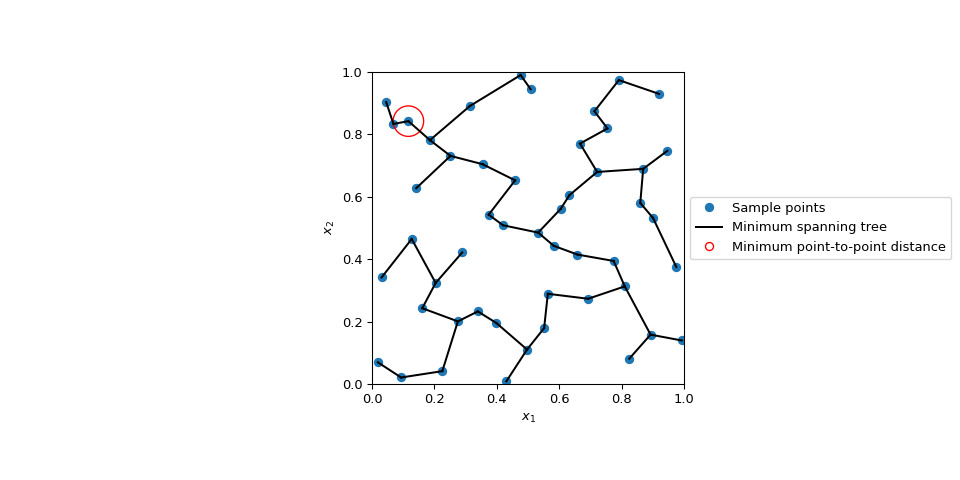
相關用法
- Python SciPy qmc.Sobol用法及代碼示例
- Python SciPy qmc.QMCEngine用法及代碼示例
- Python SciPy qmc.LatinHypercube用法及代碼示例
- Python SciPy qmc.update_discrepancy用法及代碼示例
- Python SciPy qmc.discrepancy用法及代碼示例
- Python SciPy qmc.MultinomialQMC用法及代碼示例
- Python SciPy qmc.MultivariateNormalQMC用法及代碼示例
- Python SciPy qmc.Halton用法及代碼示例
- Python SciPy qmc.scale用法及代碼示例
- Python SciPy qmc.PoissonDisk用法及代碼示例
- Python SciPy interpolate.make_interp_spline用法及代碼示例
- Python SciPy stats.anderson用法及代碼示例
- Python SciPy ClusterNode.pre_order用法及代碼示例
- Python SciPy stats.iqr用法及代碼示例
- Python SciPy FortranFile.read_record用法及代碼示例
- Python SciPy ndimage.correlate用法及代碼示例
- Python SciPy special.exp1用法及代碼示例
- Python SciPy special.expn用法及代碼示例
- Python SciPy signal.czt_points用法及代碼示例
- Python SciPy interpolate.krogh_interpolate用法及代碼示例
- Python SciPy ndimage.morphological_gradient用法及代碼示例
- Python SciPy distance.sokalmichener用法及代碼示例
- Python SciPy linalg.eigvalsh_tridiagonal用法及代碼示例
- Python SciPy linalg.cdf2rdf用法及代碼示例
- Python SciPy csc_array.diagonal用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.stats.qmc.geometric_discrepancy。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
