本文簡要介紹 python 語言中 scipy.signal.place_poles 的用法。
用法:
scipy.signal.place_poles(A, B, poles, method='YT', rtol=0.001, maxiter=30)#計算 K 使得特征值 (A - dot(B, K))=poles。
K 是增益矩陣,例如由線性係統
AX+BU說明的設備將具有其 closed-loop 極點,即特征值A - B*K,盡可能接近所要求的極點。支持 SISO、MISO 和 MIMO 係統。
- A, B: ndarray
線性係統的狀態空間表示
AX + BU。- poles: array_like
所需的實極點和/或複共軛極點。隻有
method="YT"(默認)支持複極點。- method: {‘YT’, ‘KNV0’}, optional:
選擇哪種方法來找到增益矩陣 K。其中之一:
‘YT’: Yang Tits
‘KNV0’: Kautsky, Nichols, Van Dooren update method 0
有關算法的詳細信息,請參閱引用和注釋。
- rtol: float, optional:
每次迭代後,特征向量的行列式
A - B*K當這兩個值之間的相對誤差小於rol算法停止。默認值為 1e-3。- maxiter: int, optional:
計算增益矩陣的最大迭代次數。默認值為 30。
- full_state_feedback: 束對象
- full_state_feedback 由以下部分組成:
- gain_matrix 一維ndarray
閉環矩陣K如
A-BK的特征值盡可能接近要求的極點。- computed_poles 一維ndarray
A-BK對應的極點首先按升序排列為實極點,然後按字典順序排列為複共軛。- requested_poles 一維ndarray
算法被要求放置的極點如上所示,它們可能與實現的不同。
- X 二維數組
轉移矩陣如
X * diag(poles) = (A - B*K)*X(見注釋)- rol 浮點數
實現的相對公差
det(X)(見注釋)。rol如果可以解決係統問題,將是NaNdiag(poles) = (A - B*K), 或 0 當優化算法不能做任何事情時,即當B.shape[1] == 1.- nb_iter int
收斂前執行的迭代次數。nb_iter如果可以解決係統問題,將是NaN
diag(poles) = (A - B*K), 或 0 當優化算法不能做任何事情時,即當B.shape[1] == 1.
參數 ::
返回 ::
注意:
Tits 和 Yang (YT),[2] 論文是 Kautsky 等人原始論文的更新。 (KNV)論文[1]。 KNV 依賴 1 級更新來查找傳輸矩陣 X,使得
X * diag(poles) = (A - B*K)*X,而 YT 使用 2 級更新。這平均會產生更穩健的解決方案(參見 [2] 第 21-22 頁),此外,YT 算法支持複雜極點,而 KNV 在其原始版本中不支持。這裏隻實現了 KNV 提出的更新方法 0,因此命名為'KNV0'。在 Matlab 的
place函數中使用了擴展到複極點的 KNV,YT 由 Slicot 在非自由許可下分發,名稱為robpole。目前尚不清楚 KNV0 如何擴展到複極點(Tits 和 Yang 在其論文的第 14 頁上聲稱他們的方法不能用於將 KNV 擴展到複極點),因此隻有 YT 在此實現中支持它們。由於極點放置問題的解決方案對於 MIMO 係統來說並不是唯一的,因此這兩種方法都從一個試探性的轉移矩陣開始,該矩陣以各種方式改變以增加其行列式。兩種方法都已被證明可以收斂到一個穩定的解,但是根據選擇初始傳遞矩陣的方式,它們將收斂到不同的解,因此絕對不能保證使用
'KNV0'會產生類似於 Matlab 或任何其他方法的結果這些算法的實現。在大多數情況下,使用默認方法
'YT'應該沒問題;僅提供'KNV0'是因為在某些特定情況下'YT'需要它。此外,當abs(det(X))用作穩健性指標時,'YT'給出的平均結果比'KNV0'更穩健。[2] 可通過以下 URL 獲取技術報告:https://hdl.handle.net/1903/5598
參考:
[1] (1,2)J.考茨基,N.K. Nichols 和 P. van Dooren,“線性狀態反饋中的魯棒極點分配”,國際控製雜誌,卷。 1985 年,第 41 頁,第 1129-1155 頁。
[2] (1,2,3)A.L. Tits 和 Y. Yang,“通過狀態反饋進行穩健極點分配的全局收斂算法”,IEEE Transactions on Automatic Control,Vol。 41,第 1432-1452 頁,1996。
例子:
一個使用 KNV 和 YT 算法演示實際極點放置的簡單示例。這是參考 KNV 出版物 ([1]) 第 4 節中的示例編號 1:
>>> import numpy as np >>> from scipy import signal >>> import matplotlib.pyplot as plt>>> A = np.array([[ 1.380, -0.2077, 6.715, -5.676 ], ... [-0.5814, -4.290, 0, 0.6750 ], ... [ 1.067, 4.273, -6.654, 5.893 ], ... [ 0.0480, 4.273, 1.343, -2.104 ]]) >>> B = np.array([[ 0, 5.679 ], ... [ 1.136, 1.136 ], ... [ 0, 0, ], ... [-3.146, 0 ]]) >>> P = np.array([-0.2, -0.5, -5.0566, -8.6659])現在使用 KNV 方法 0、默認 YT 方法和 YT 方法計算 K,同時強製算法迭代 100 次,並在每次調用後打印一些結果。
>>> fsf1 = signal.place_poles(A, B, P, method='KNV0') >>> fsf1.gain_matrix array([[ 0.20071427, -0.96665799, 0.24066128, -0.10279785], [ 0.50587268, 0.57779091, 0.51795763, -0.41991442]])>>> fsf2 = signal.place_poles(A, B, P) # uses YT method >>> fsf2.computed_poles array([-8.6659, -5.0566, -0.5 , -0.2 ])>>> fsf3 = signal.place_poles(A, B, P, rtol=-1, maxiter=100) >>> fsf3.X array([[ 0.52072442+0.j, -0.08409372+0.j, -0.56847937+0.j, 0.74823657+0.j], [-0.04977751+0.j, -0.80872954+0.j, 0.13566234+0.j, -0.29322906+0.j], [-0.82266932+0.j, -0.19168026+0.j, -0.56348322+0.j, -0.43815060+0.j], [ 0.22267347+0.j, 0.54967577+0.j, -0.58387806+0.j, -0.40271926+0.j]])X 行列式的絕對值是檢查結果穩健性的一個很好的指標,
'KNV0'和'YT'都旨在最大化它。下麵對比上述結果的穩健性:>>> abs(np.linalg.det(fsf1.X)) < abs(np.linalg.det(fsf2.X)) True >>> abs(np.linalg.det(fsf2.X)) < abs(np.linalg.det(fsf3.X)) True現在是複雜極點的簡單示例:
>>> A = np.array([[ 0, 7/3., 0, 0 ], ... [ 0, 0, 0, 7/9. ], ... [ 0, 0, 0, 0 ], ... [ 0, 0, 0, 0 ]]) >>> B = np.array([[ 0, 0 ], ... [ 0, 0 ], ... [ 1, 0 ], ... [ 0, 1 ]]) >>> P = np.array([-3, -1, -2-1j, -2+1j]) / 3. >>> fsf = signal.place_poles(A, B, P, method='YT')我們可以在複平麵上繪製所需和計算的極點:
>>> t = np.linspace(0, 2*np.pi, 401) >>> plt.plot(np.cos(t), np.sin(t), 'k--') # unit circle >>> plt.plot(fsf.requested_poles.real, fsf.requested_poles.imag, ... 'wo', label='Desired') >>> plt.plot(fsf.computed_poles.real, fsf.computed_poles.imag, 'bx', ... label='Placed') >>> plt.grid() >>> plt.axis('image') >>> plt.axis([-1.1, 1.1, -1.1, 1.1]) >>> plt.legend(bbox_to_anchor=(1.05, 1), loc=2, numpoints=1)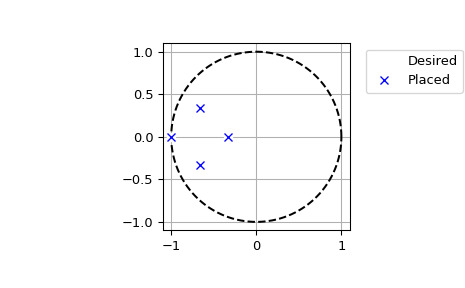
相關用法
- Python SciPy signal.peak_widths用法及代碼示例
- Python SciPy signal.peak_prominences用法及代碼示例
- Python SciPy signal.periodogram用法及代碼示例
- Python SciPy signal.czt_points用法及代碼示例
- Python SciPy signal.chirp用法及代碼示例
- Python SciPy signal.residue用法及代碼示例
- Python SciPy signal.iirdesign用法及代碼示例
- Python SciPy signal.max_len_seq用法及代碼示例
- Python SciPy signal.kaiser_atten用法及代碼示例
- Python SciPy signal.oaconvolve用法及代碼示例
- Python SciPy signal.hilbert用法及代碼示例
- Python SciPy signal.ricker用法及代碼示例
- Python SciPy signal.group_delay用法及代碼示例
- Python SciPy signal.cheb2ord用法及代碼示例
- Python SciPy signal.get_window用法及代碼示例
- Python SciPy signal.lfilter用法及代碼示例
- Python SciPy signal.morlet用法及代碼示例
- Python SciPy signal.coherence用法及代碼示例
- Python SciPy signal.dfreqresp用法及代碼示例
- Python SciPy signal.TransferFunction用法及代碼示例
- Python SciPy signal.dbode用法及代碼示例
- Python SciPy signal.residuez用法及代碼示例
- Python SciPy signal.bilinear_zpk用法及代碼示例
- Python SciPy signal.firls用法及代碼示例
- Python SciPy signal.impulse用法及代碼示例
注:本文由純淨天空篩選整理自scipy.org大神的英文原創作品 scipy.signal.place_poles。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
