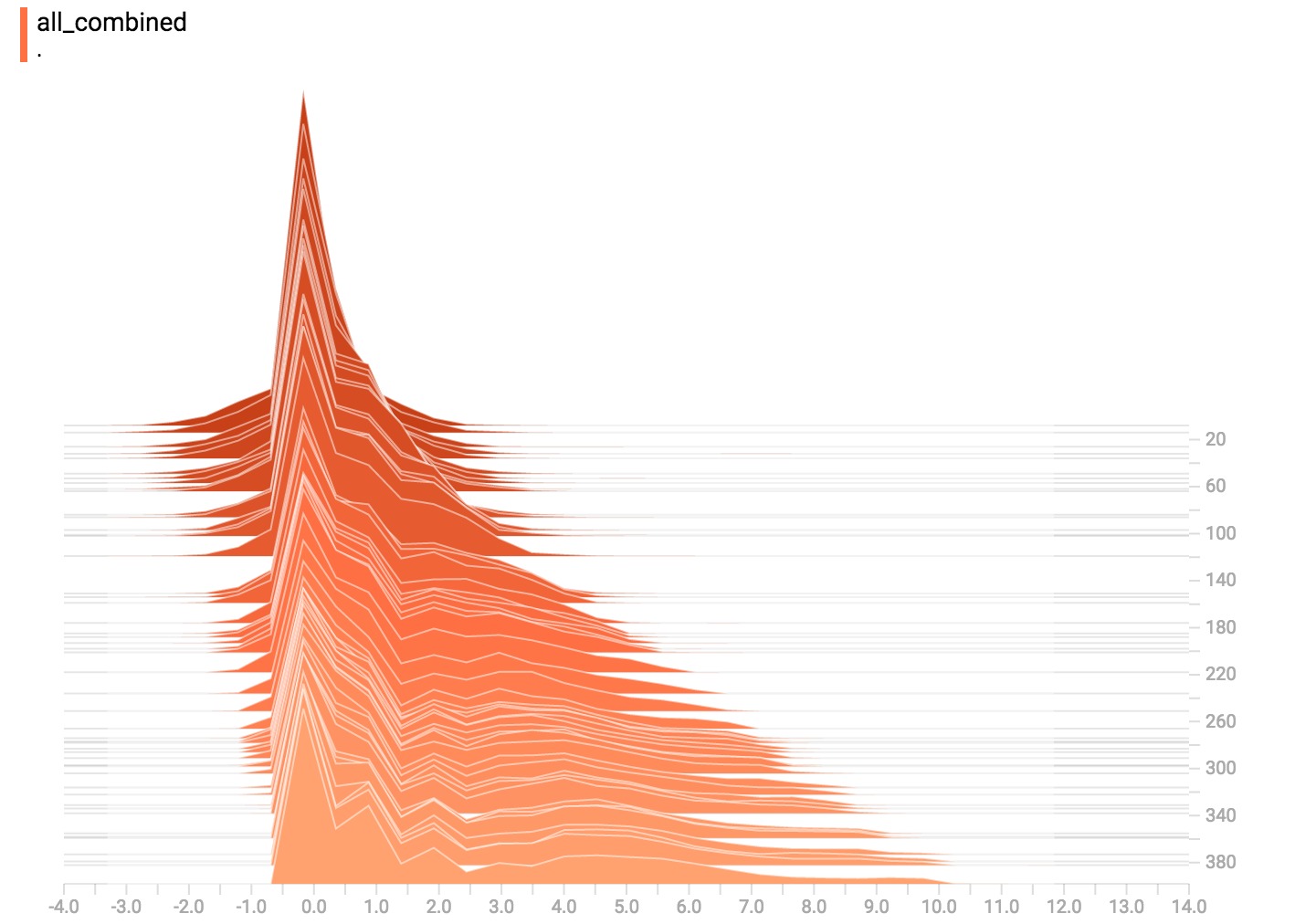
TensorBoard直方圖儀表板用於顯示Tensor的分布,這些分布對應到TensorFlow圖計算的不同時刻。它通過在不同的時間點顯示張量的直方圖可視化來實現這一點。
一個基本的例子
讓我們從一個簡單的例子開始:一個正態分布變量,其中平均值隨時間變化。 TensorFlow有一個操作:tf.random_normal,可以完美的用於這個目的。與TensorBoard通常情況一樣,我們將使用‘tf.summary.histogram’摘要操作來獲取數據。有關summary如何工作的初步介紹,請參TensorBoard教程。
這是一個代碼片段,它將生成一些包含正態分布數據的直方圖摘要,其中分布的均值隨時間而增加。
import tensorflow as tf
k = tf.placeholder(tf.float32)
# Make a normal distribution, with a shifting mean
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# Record that distribution into a histogram summary
tf.summary.histogram("normal/moving_mean", mean_moving_normal)
# Setup a session and summary writer
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")
summaries = tf.summary.merge_all()
# Setup a loop and write the summaries to disk
N = 400
for step in range(N):
k_val = step/float(N)
summ = sess.run(summaries, feed_dict={k: k_val})
writer.add_summary(summ, global_step=step)
一旦代碼運行,我們可以通過命令行將數據加載到TensorBoard中:
tensorboard --logdir=/tmp/histogram_example
一旦TensorBoard正在運行,在Chrome或Firefox中打開localhost:6006,然後導航到“柱狀圖”控製麵板。然後我們可以看到正態分布數據的直方圖。
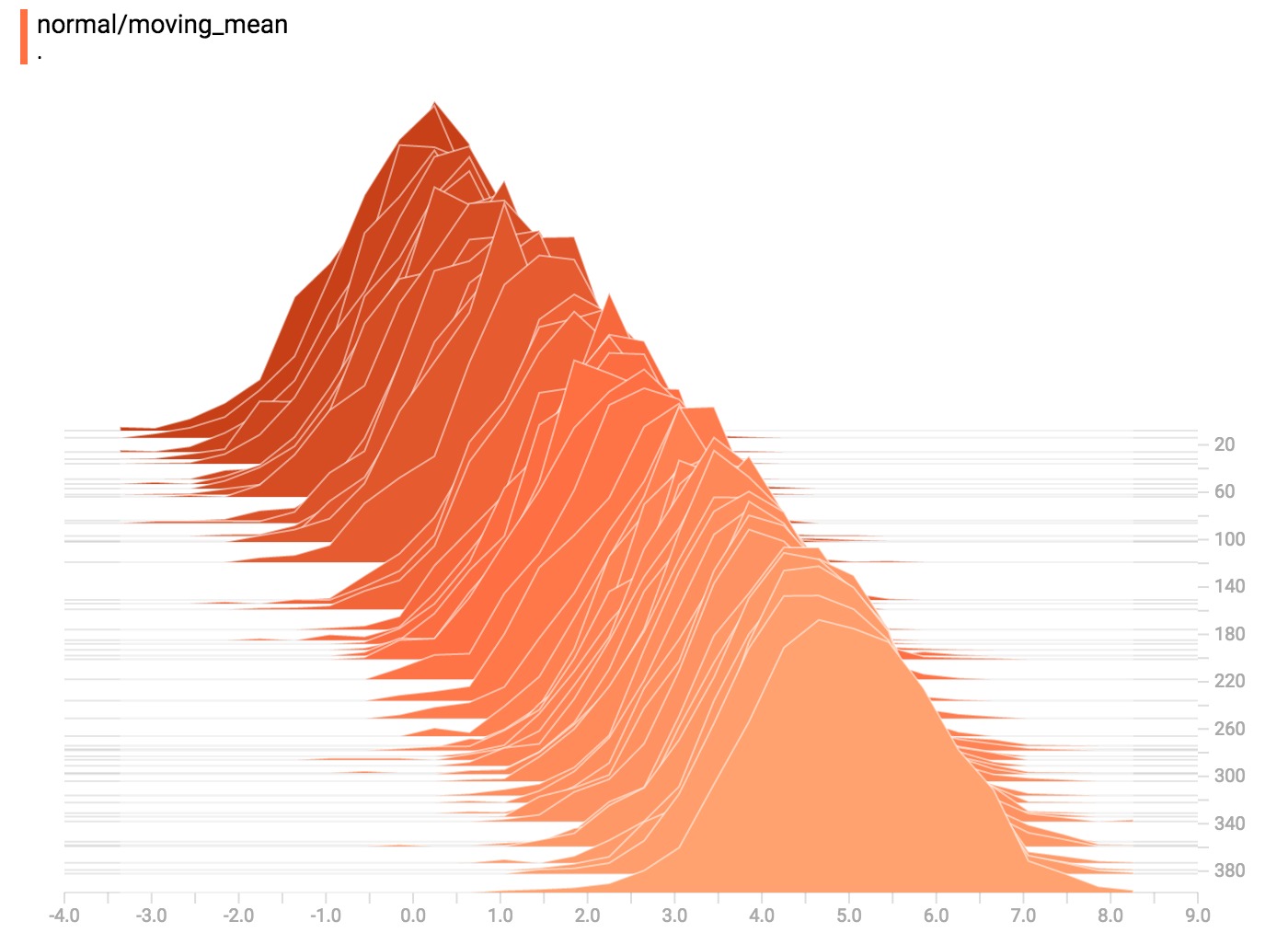
tf.summary.histogram以一個任意大小和形狀的張量作為參數,將其壓縮成一個由寬度和數量組成的直方圖數據結構。例如,假設我們要把數字[0.5, 1.1, 1.3, 2.2, 2.9, 2.99]分配到bin中。可以設計三個bin:一個bin包含從0到1的所有內容(它將包含一個元素,0.5),一個包含1-2(包含兩個元素,1.1和1.3)的所有內容的bin,*一個包含2-3的所有內容的bin(它將包含三個元素:2.2,2.9和2.99)。
TensorFlow使用類似的方法來創建分檔,但與我們的例子不同,它不會創建整數分檔。對於大而稀疏的數據集,可能會導致數千個分檔。替代方案:bins呈指數分布,許多bins接近於0,對於較大數字的bins比較少。然而,可視化指數分布的bins是棘手的;如果使用高度來編碼計數,那麽即使具有相同數量的元素,較寬的bins也需要更多的空間。相反,在該區域的編碼計數也不能用高度比較。因此,直方圖重新采樣數據到統一的bins。
直方圖可視化器中的每個切片顯示單個直方圖。切片按步驟組織;較舊的切片(例如步驟0)靠後且較暗,而較新的切片(例如,步驟400)靠前且顏色較淺。右側的y-axis顯示步驟編號。
您可以將鼠標懸停在直方圖上,查看更多詳細信息。例如,在下麵的圖像中,我們可以看到步驟176中的直方圖具有以2.25為中心的bin,該bin中有177個元素。
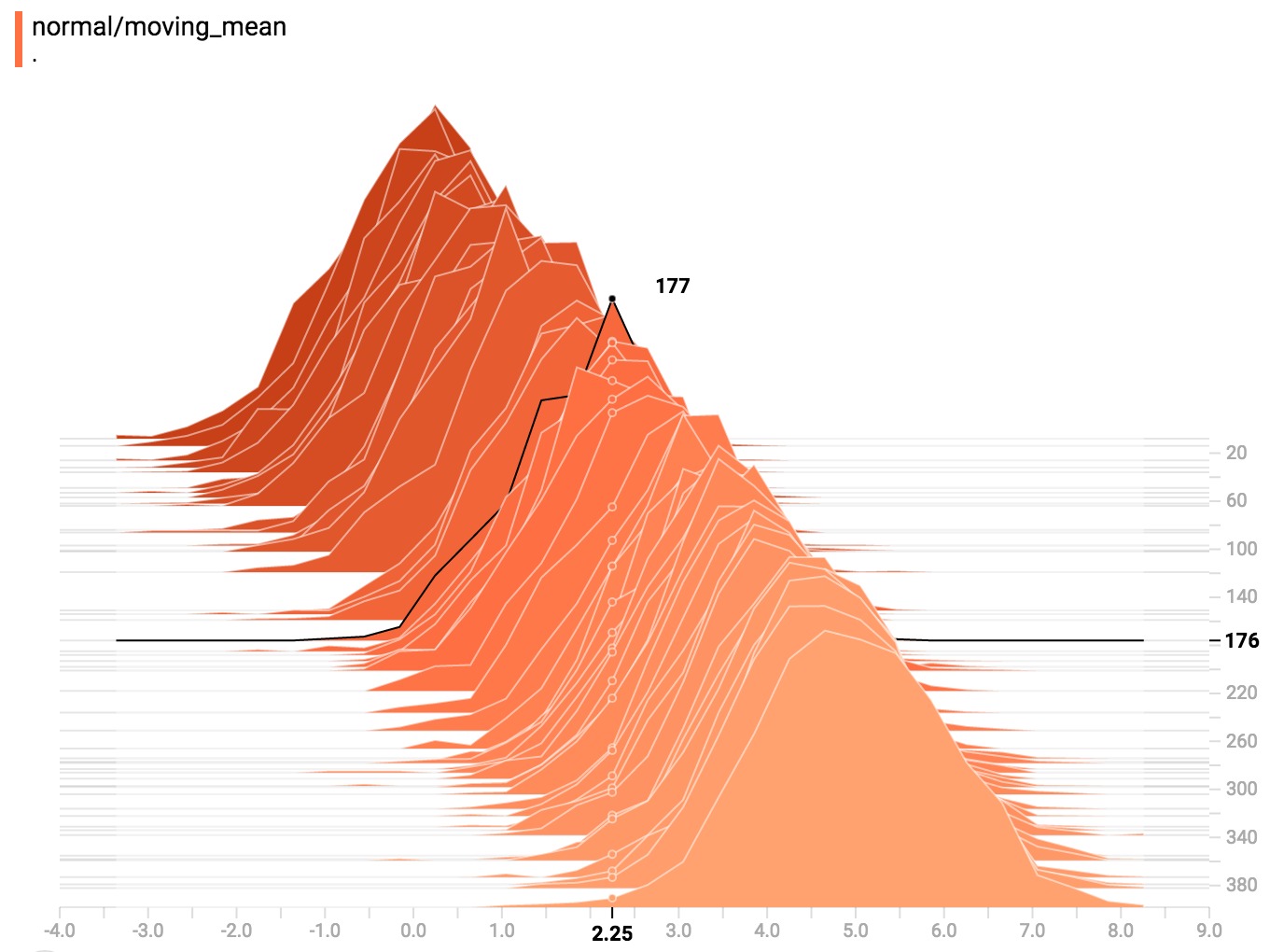
此外,您可能會注意到,直方圖切片並不總是以步驟計數或時間間隔均勻分布。這是因為TensorBoard使用蓄水池采樣保留所有直方圖的一個子集,以節省內存。蓄水池采樣保證每個樣本都有相同的被包含的可能性,但是因為它是一個隨機算法,選擇的樣本不會在每一步中出現。
覆蓋模式
儀表板左側有一個控件,可以將直方圖模式從”offset”切換到”overlay”:
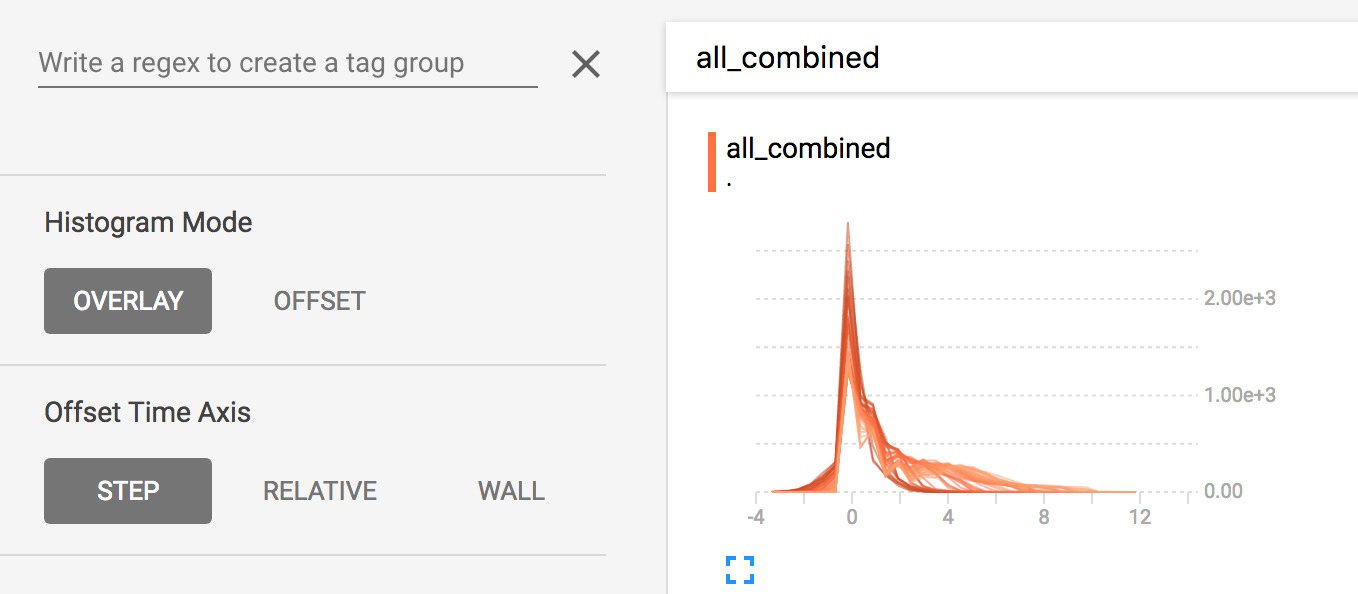
在”offset”模式下,可視化旋轉45度,以便各個直方圖切片不再按時間展開,而是全部繪製在相同的y-axis上。
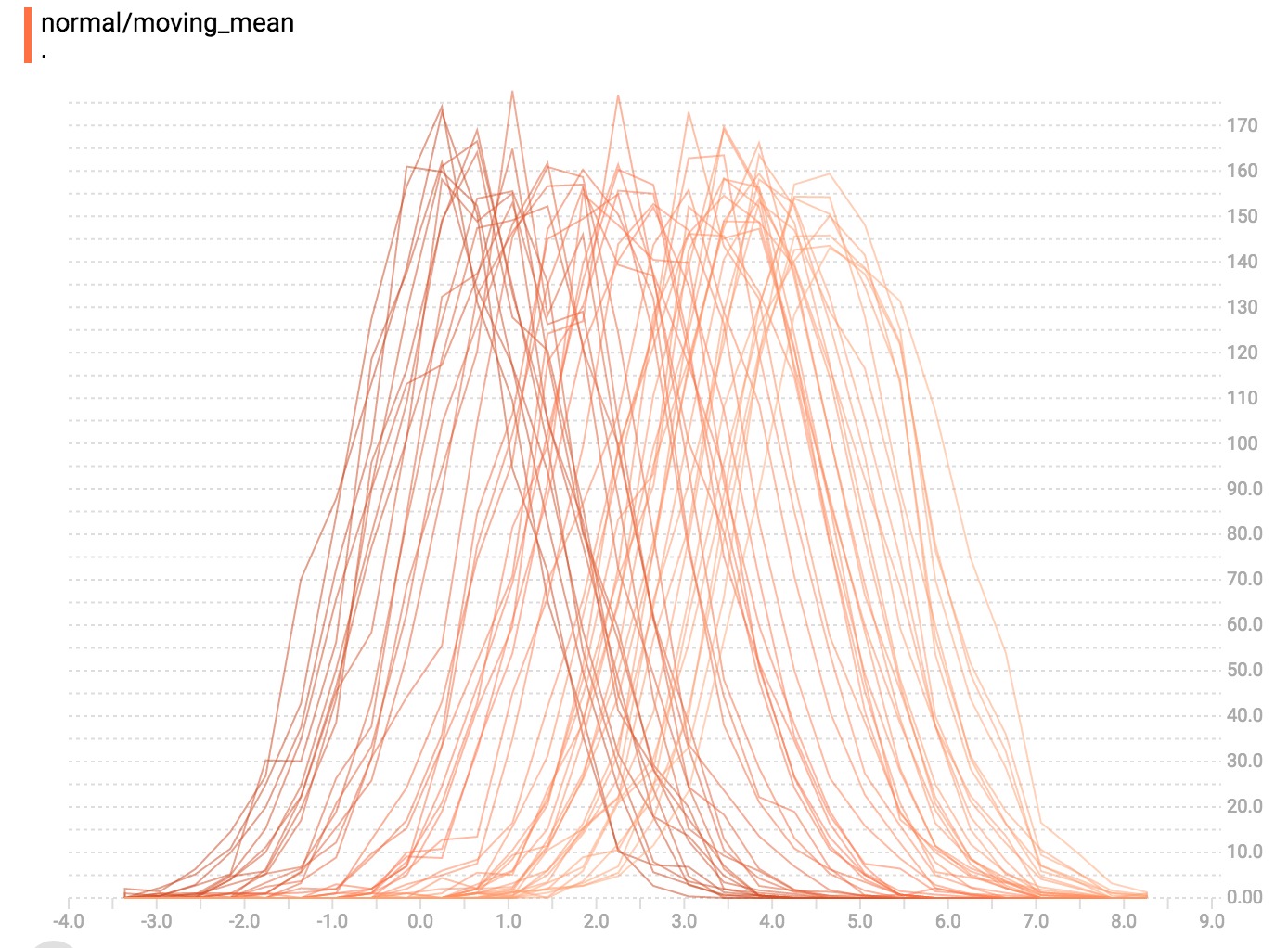 現在,每個切片都是圖表上的一個單獨的行,y-axis顯示每個桶內的項目數。較深的線條對應較舊、較早的步驟,較輕,較淺的線條對應較近、剛剛的步驟,您可以將鼠標懸停在圖表上以查看其他信息。
現在,每個切片都是圖表上的一個單獨的行,y-axis顯示每個桶內的項目數。較深的線條對應較舊、較早的步驟,較輕,較淺的線條對應較近、剛剛的步驟,您可以將鼠標懸停在圖表上以查看其他信息。
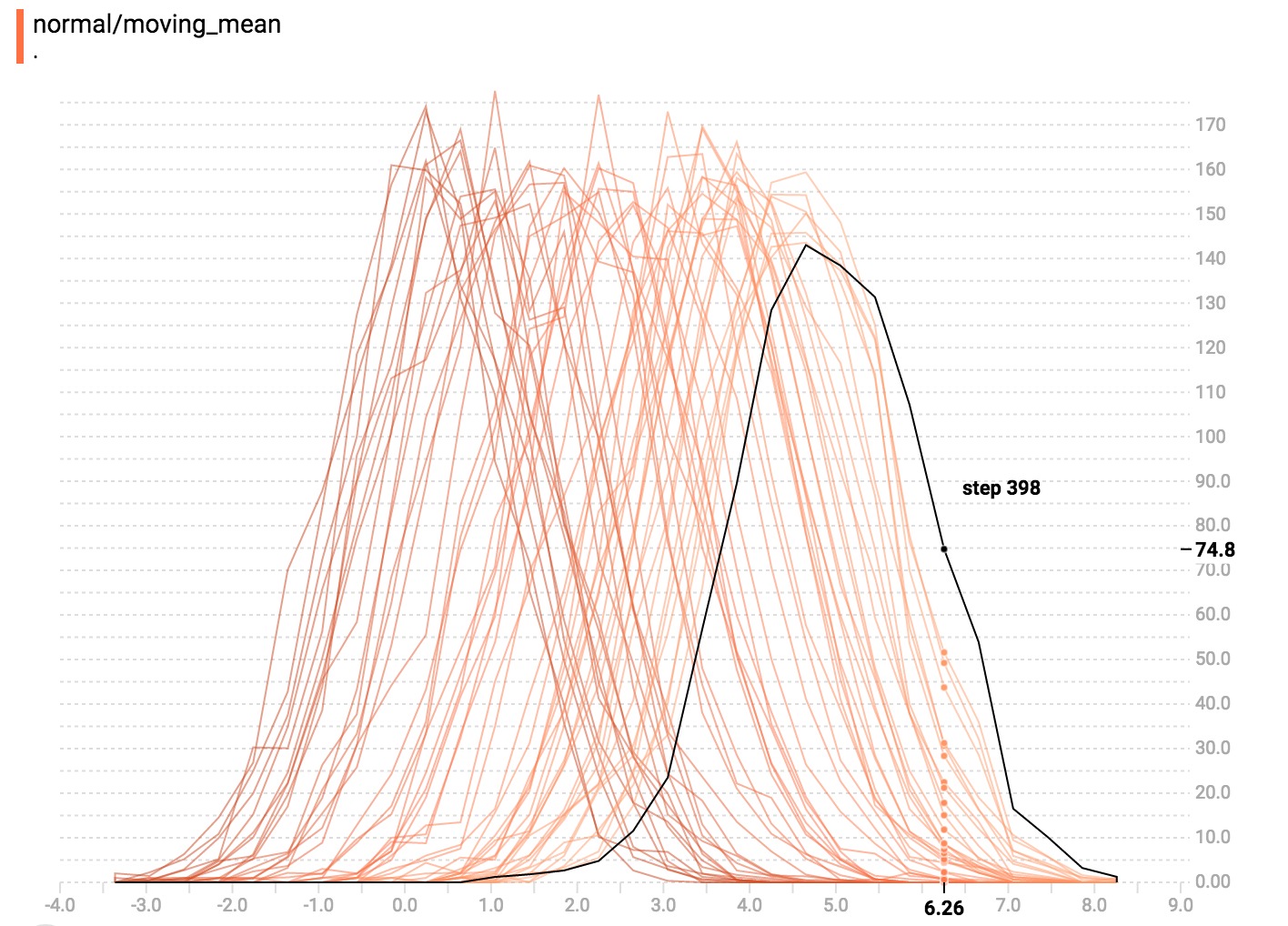
一般來說,如果要直接比較不同直方圖的計數,覆蓋模式的可視化將非常有用。
多峰分配
直方圖儀表板非常適合可視化多峰分布。讓我們通過連接兩個不同的正態分布的輸出來構造一個簡單的雙峰分布。代碼將如下所示:
import tensorflow as tf
k = tf.placeholder(tf.float32)
# Make a normal distribution, with a shifting mean
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# Record that distribution into a histogram summary
tf.summary.histogram("normal/moving_mean", mean_moving_normal)
# Make a normal distribution with shrinking variance
variance_shrinking_normal = tf.random_normal(shape=[1000], mean=0, stddev=1-(k))
# Record that distribution too
tf.summary.histogram("normal/shrinking_variance", variance_shrinking_normal)
# Let's combine both of those distributions into one dataset
normal_combined = tf.concat([mean_moving_normal, variance_shrinking_normal], 0)
# We add another histogram summary to record the combined distribution
tf.summary.histogram("normal/bimodal", normal_combined)
summaries = tf.summary.merge_all()
# Setup a session and summary writer
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")
# Setup a loop and write the summaries to disk
N = 400
for step in range(N):
k_val = step/float(N)
summ = sess.run(summaries, feed_dict={k: k_val})
writer.add_summary(summ, global_step=step)
從上麵的例子,可以想到之前的”moving mean”正態分布。現在我們有一個”shrinking variance”(改變方差)發行版本。他們並列看起來像這樣: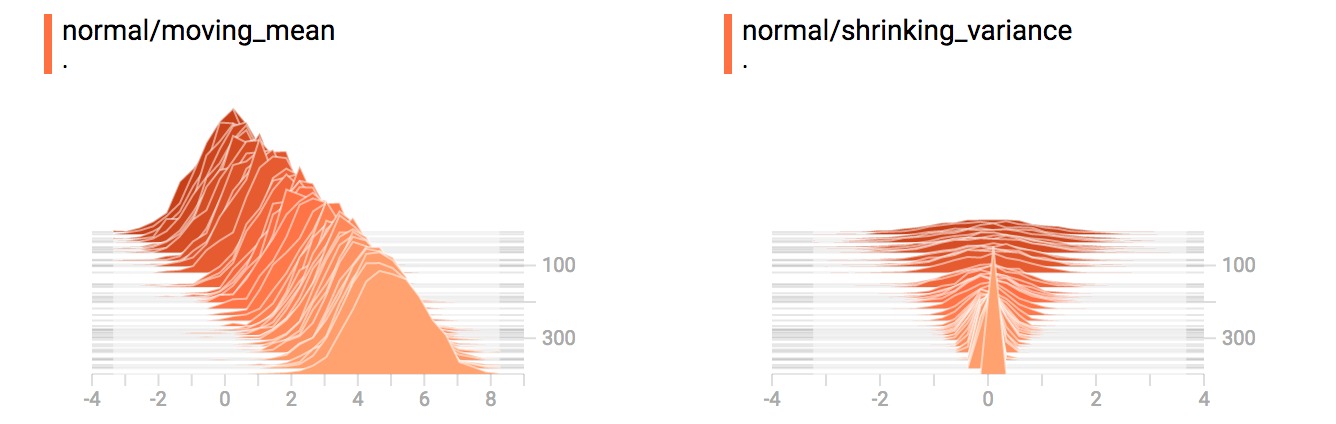
當我們把它們連接起來的時候,我們得到一個清楚地顯示出不同的雙峰結構的圖表: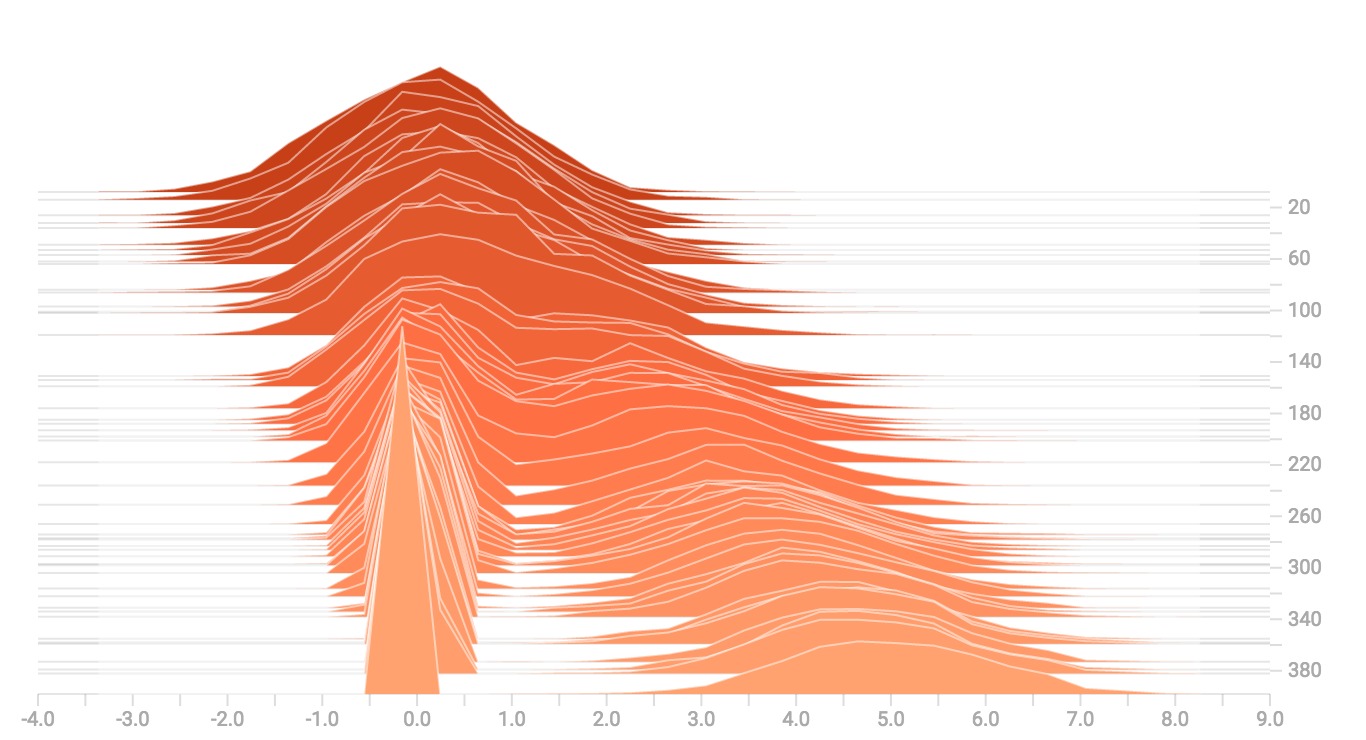
更多的分布
為了好玩,讓我們生成和可視化更多的分布,然後將它們合並成一個圖表。以下是我們將使用的代碼:
import tensorflow as tf
k = tf.placeholder(tf.float32)
# Make a normal distribution, with a shifting mean
mean_moving_normal = tf.random_normal(shape=[1000], mean=(5*k), stddev=1)
# Record that distribution into a histogram summary
tf.summary.histogram("normal/moving_mean", mean_moving_normal)
# Make a normal distribution with shrinking variance
variance_shrinking_normal = tf.random_normal(shape=[1000], mean=0, stddev=1-(k))
# Record that distribution too
tf.summary.histogram("normal/shrinking_variance", variance_shrinking_normal)
# Let's combine both of those distributions into one dataset
normal_combined = tf.concat([mean_moving_normal, variance_shrinking_normal], 0)
# We add another histogram summary to record the combined distribution
tf.summary.histogram("normal/bimodal", normal_combined)
# Add a gamma distribution
gamma = tf.random_gamma(shape=[1000], alpha=k)
tf.summary.histogram("gamma", gamma)
# And a poisson distribution
poisson = tf.random_poisson(shape=[1000], lam=k)
tf.summary.histogram("poisson", poisson)
# And a uniform distribution
uniform = tf.random_uniform(shape=[1000], maxval=k*10)
tf.summary.histogram("uniform", uniform)
# Finally, combine everything together!
all_distributions = [mean_moving_normal, variance_shrinking_normal,
gamma, poisson, uniform]
all_combined = tf.concat(all_distributions, 0)
tf.summary.histogram("all_combined", all_combined)
summaries = tf.summary.merge_all()
# Setup a session and summary writer
sess = tf.Session()
writer = tf.summary.FileWriter("/tmp/histogram_example")
# Setup a loop and write the summaries to disk
N = 400
for step in range(N):
k_val = step/float(N)
summ = sess.run(summaries, feed_dict={k: k_val})
writer.add_summary(summ, global_step=step)
伽瑪分布
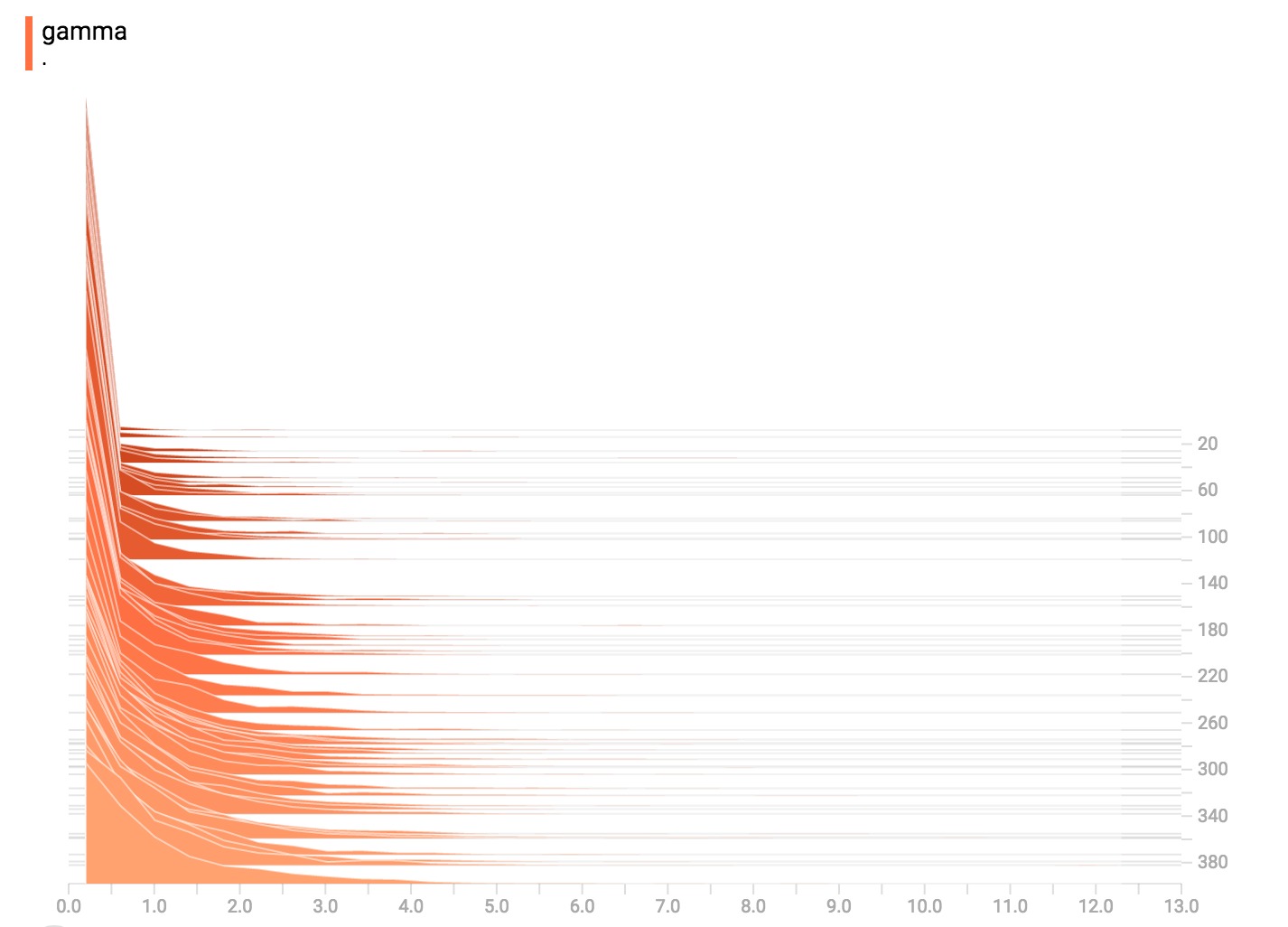
均勻分配

泊鬆分布
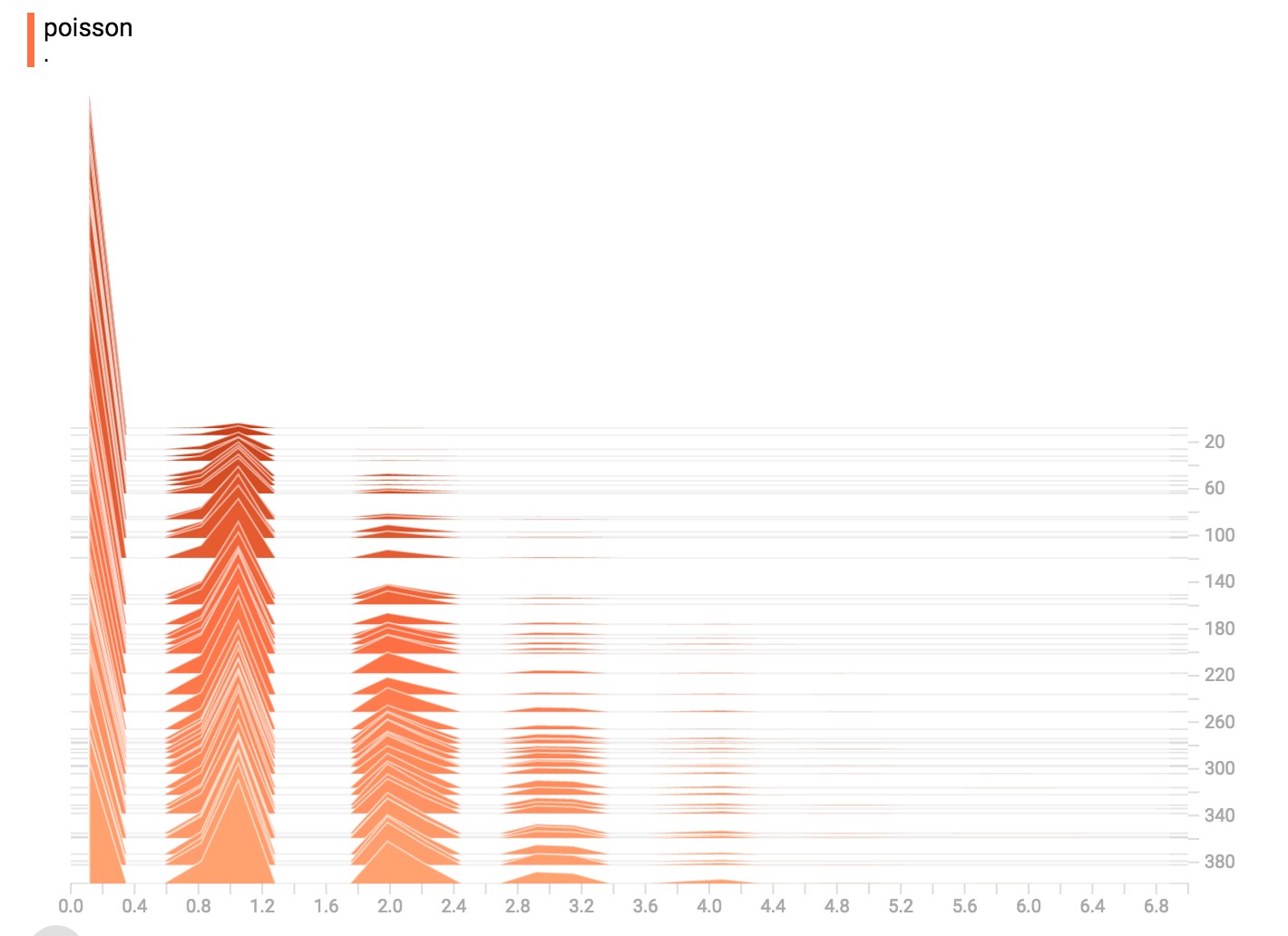 泊鬆分布是在整數上定義的。所以,所有生成的值都是完美的整數。直方圖壓縮將數據移動到浮點數分割的bin中,導致可視化在整數值上顯示出很小的隆起,而不是完美的尖峰。
泊鬆分布是在整數上定義的。所以,所有生成的值都是完美的整數。直方圖壓縮將數據移動到浮點數分割的bin中,導致可視化在整數值上顯示出很小的隆起,而不是完美的尖峰。
現在都在一起了
最後,我們可以將所有的數據連接成一個好玩的曲線。