Python numpy RandomState.normal用法及代码示例

本文简要介绍 python 语言中 numpy.random.RandomState.normal 的用法。

用法:

random.RandomState.normal(loc=0.0, scale=1.0, size=None)

从正态(高斯)分布中抽取随机样本。

正态分布的概率密度函数首先由 De Moivre 导出，200 年后由 Gauss 和 Laplace [2] 独立导出，由于其特征形状，通常被称为钟形曲线(参见下面的示例)。

正态分布在自然界中经常发生。例如，它说明了受大量微小随机扰动影响的样本的普遍分布，每个扰动都有其独特的分布 [2]。

注意

新代码应改为使用default_rng() 实例的normal 方法；请参阅快速入门。

参数：

loc： 浮点数或类似数组的浮点数

分布的平均值 (“centre”)。

scale： 浮点数或类似数组的浮点数

分布的标准差(spread 或“width”)。必须是非负数。

size： int 或整数元组，可选

输出形状。例如，如果给定的形状是 (m, n, k) ，则绘制 m * n * k 样本。如果 size 为 None(默认)，如果 loc 和 scale 都是标量，则返回单个值。否则，将抽取np.broadcast(loc, scale).size 样本。

返回：

out： ndarray 或标量

从参数化正态分布中抽取样本。

注意：

高斯分布的概率密度为

\[p(x) = \frac{1}{\sqrt{ 2 \pi \sigma^2 }} e^{ - \frac{ (x - \mu)^2 } {2 \sigma^2} },\]

其中\(\mu\) 是平均值，\(\sigma\) 是标准差。标准差的平方 \(\sigma^2\) 称为方差。

该函数在平均值处达到峰值，并且其 “spread” 随着标准差的增加而增加(该函数在 \(x + \sigma\) 和 \(x - \sigma\) 处达到其最大值的 0.607 倍 [2])。这意味着正态更有可能返回接近均值的样本，而不是远离均值的样本。

参考：

1：

维基百科，“Normal distribution”，https://en.wikipedia.org/wiki/Normal_distribution

2 (1,2,3)：

P. R. Peebles Jr.，“Central Limit Theorem”，“概率、随机变量和随机信号原理”，第 4 版，2001 年，第 51、51、125 页。

例子：

从分布中抽取样本：

>>> mu, sigma = 0, 0.1 # mean and standard deviation
>>> s = np.random.normal(mu, sigma, 1000)

验证均值和方差：

>>> abs(mu - np.mean(s))
0.0  # may vary

>>> abs(sigma - np.std(s, ddof=1))
0.1  # may vary

显示样本的直方图以及概率密度函数：

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 30, density=True)
>>> plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
...                np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
...          linewidth=2, color='r')
>>> plt.show()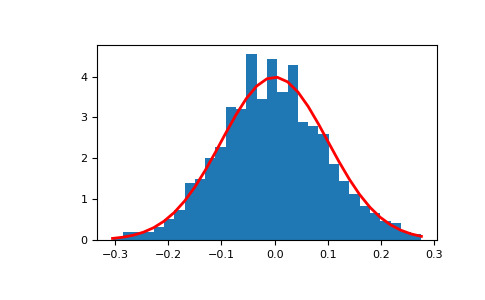

Two-by-four 来自 N(3, 6.25) 的样本数组：

>>> np.random.normal(3, 2.5, size=(2, 4))
array([[-4.49401501,  4.00950034, -1.81814867,  7.29718677],   # random
       [ 0.39924804,  4.68456316,  4.99394529,  4.84057254]])  # random