这篇文章将向您展示如何：

使用高斯核估计2个分布的PDF(PDF即Probability Density Function，概率密度函数)
使用Matplotlib表示PDF，其中密度图周围带有标记的轮廓线
如何提取轮廓线
如何在3D(3维空间)中绘制上述高斯核
如何使用2D直方图绘制相同的PDF

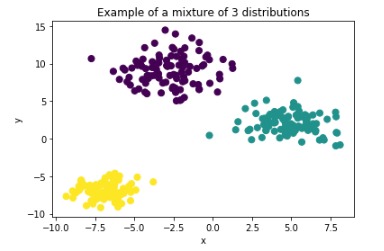
首先，生成由3个blob组成的输入数据集：(关于blob：scikit中的make_blobs方法常被用来生成聚类算法的测试数据，直观地说，make_blobs会根据用户指定的特征数量、中心点数量、范围等来生成几类数据，这些数据可用于测试聚类算法的效果。）

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st
from sklearn.datasets.samples_generator import make_blobsn_components = 3
X, truth = make_blobs(n_samples=300, centers=n_components, 
                      cluster_std = [2, 1.5, 1], 
                      random_state=42)plt.scatter(X[:, 0], X[:, 1], s=50, c = truth)
plt.title(f"Example of a mixture of {n_components} distributions")
plt.xlabel("x")
plt.ylabel("y");

为了拟合高斯核，我们指定了一个网格，该网格将在每个轴上使用100点插值(例如mgrid(xmin：xmax：100j))：

# Extract x and y
x = X[:, 0]
y = X[:, 1]# Define the borders
deltaX = (max(x) - min(x))/10
deltaY = (max(y) - min(y))/10xmin = min(x) - deltaX
xmax = max(x) + deltaXymin = min(y) - deltaY
ymax = max(y) + deltaYprint(xmin, xmax, ymin, ymax)# Create meshgrid
xx, yy = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]

我们将使用scipy的gaussian_kde方法拟合高斯核：

positions = np.vstack([xx.ravel(), yy.ravel()])
values = np.vstack([x, y])
kernel = st.gaussian_kde(values)
f = np.reshape(kernel(positions).T, xx.shape)

用带注释的轮廓绘制核

fig = plt.figure(figsize=(8,8))
ax = fig.gca()
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
cfset = ax.contourf(xx, yy, f, cmap='coolwarm')
ax.imshow(np.rot90(f), cmap='coolwarm', extent=[xmin, xmax, ymin, ymax])
cset = ax.contour(xx, yy, f, colors='k')
ax.clabel(cset, inline=1, fontsize=10)
ax.set_xlabel('X')
ax.set_ylabel('Y')
plt.title('2D Gaussian Kernel density estimation')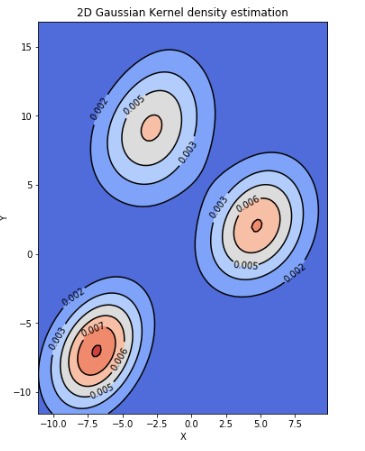

这个matplotlib对象称为QuadContour set(设置在代码中)。我们可以通过迭代访问allsegs对象以编程方式访问等高线。可从labelTexts访问计算出的标签。

plt.figure(figsize=(8,8))for j in range(len(cset.allsegs)):
    for ii, seg in enumerate(cset.allsegs[j]):
        plt.plot(seg[:,0], seg[:,1], '.-', label=f'Cluster{j}, level{ii}')plt.legend()

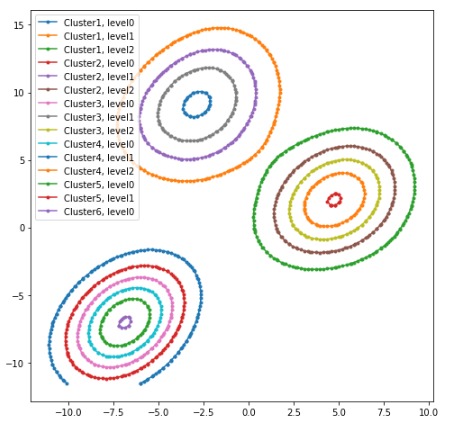
3D KDE图

我们将使用matplotlib的axis3d(来自mplot3d)。可以将密度绘制为曲面：

fig = plt.figure(figsize=(13, 7))
ax = plt.axes(projection='3d')
surf = ax.plot_surface(xx, yy, f, rstride=1, cstride=1, cmap='coolwarm', edgecolor='none')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('PDF')
ax.set_title('Surface plot of Gaussian 2D KDE')
fig.colorbar(surf, shrink=0.5, aspect=5) # add color bar indicating the PDF
ax.view_init(60, 35)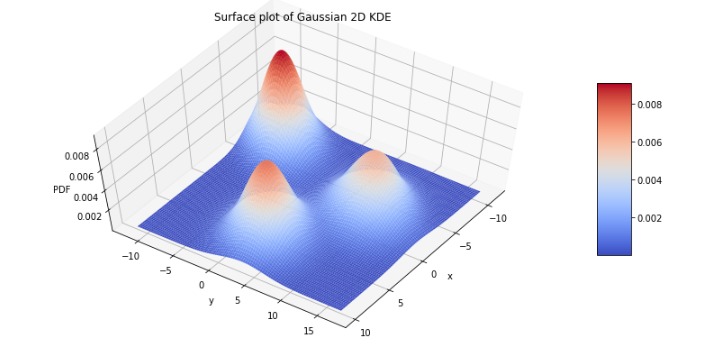

或作为线框：

fig = plt.figure(figsize=(13, 7))
ax = plt.axes(projection='3d')
w = ax.plot_wireframe(xx, yy, f)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('PDF')
ax.set_title('Wireframe plot of Gaussian 2D KDE');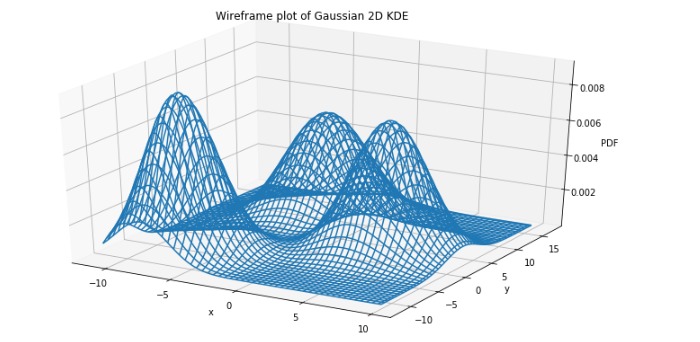

使用2D直方图表示

呈现相同信息的另一种方法是使用2D直方图。设定参数normed = False将返回实际频率，设为True将返回PDF(概率密度函数)。

h =plt.hist2d(x, y)
plt.colorbar(h[3])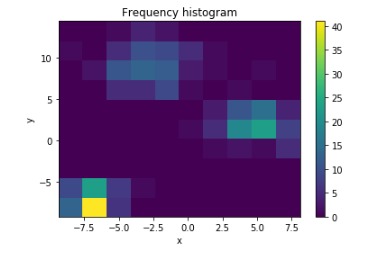

本文的完整的代码可在Github找到。

python二维密度图的例程

用带注释的轮廓绘制核

3D KDE图

参考资料