算法
如前所述,t-SNE采用高维数据集,并将其简化为保留了许多原始信息的低维图。
假设我们有一个由3个不同的类组成的数据集。
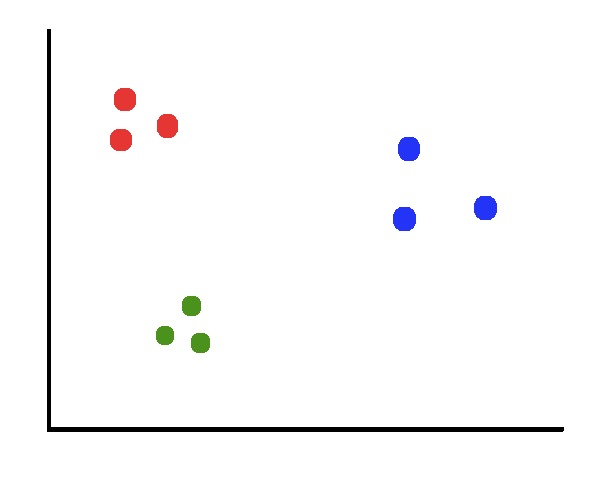
我们希望将2D图简化为1D图,同时保持群集之间的清晰边界。
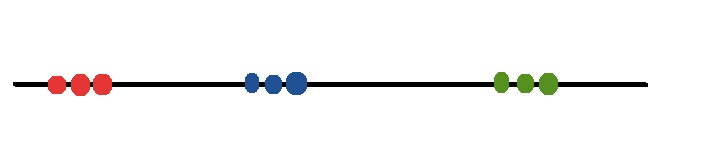
回想一下,仅将数据投影到轴上是降低维数的一种较差的方法,因为我们会丢失大量信息。

相反,我们可以使用降维技术(提示:t-SNE)来实现所需的功能。 t-SNE算法的第一步涉及测量从一个点到另一个点的距离。而不是直接处理距离,我们将它们映射到概率分布。
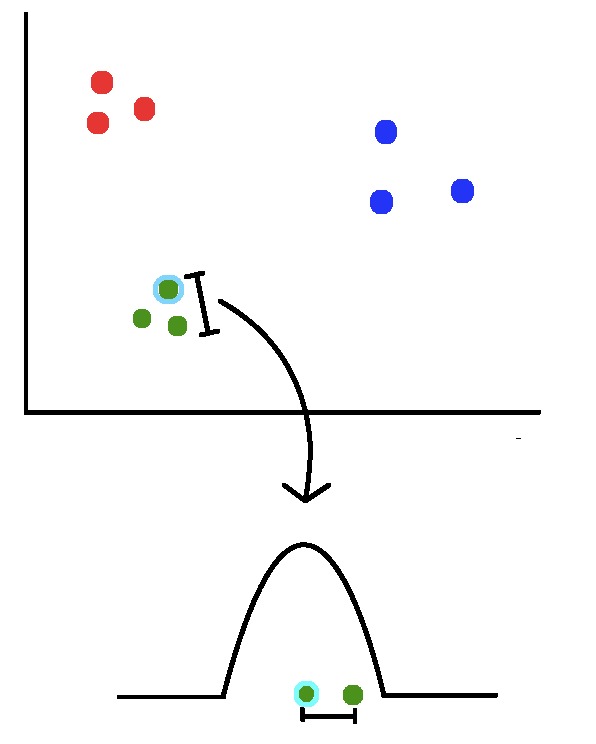
在分布中,相对于当前点距离最小的点的可能性很高,而远离当前点的点的可能性很低。

再看一下2D图,请注意蓝色簇比绿色簇更分散。如果我们不解决这种尺度差异,则绿点的可能性将大于蓝点的可能性。为了说明这个事实,我们用可能性之和做归一化。

因此,尽管两点之间的绝对距离不同,但它们被认为是相似的。
让我们尝试将这些概念与基础理论联系起来。在数学上,我们将正态分布的方程写为如下形式:
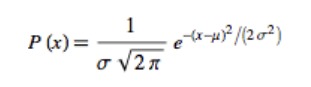
如果我们将所有项都做指数计算,并使用另一个点代替均值,同时用求和规归一化解决前面讨论的尺度问题,得到如下公式(参考论文)。

接下来,我们考虑降维到低维空间的情形。首先,我们创建一个n_samples x n_components的矩阵(在这种情况下为9×1)并用随机值(即位置)填充。

如果我们对上述情况采取类似的方法(测量点之间的距离并将其映射到概率分布),则可以得到以下等式。
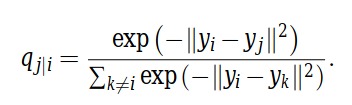
请注意,就像以前一样,我们采用正态分布方程式,将所有内容放在前面,使用其他点代替均值,然后通过除以所有其他点的似然之和来解决尺度问题(这里忽略了标准差)。
如果我们能使降维后特征空间中的点的概率分布近似于原始特征空间中的点的概率分布,则可以得到定义良好的聚类。

为此,我们使用了称为Kullback-Leiber散度的东西。 KL散度是一个概率分布与另一个概率分布之间差异的度量。

KL散度的值越小,两个分布之间的距离越近。 KL散度为0表示所讨论的两个分布是相同的。
回想一下在线性回归的情况下,我们如何通过使用梯度下降来最小化损失函数(即均方误差)来确定最佳拟合曲线。在t-SNE中,我们同样使用梯度下降法将所有数据点上Kullback-Leiber散度的总和最小化。


针对每个点取成本函数的偏导数,以便提供每次更新的方向。
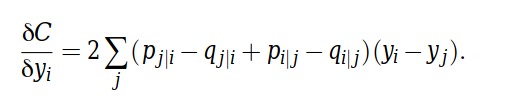
t-SNE的Python代码
在接下来的部分中,我将尝试将算法和相关的数学方程式实现为Python代码。为了完成该过程,我从scikit-learn 源代码的TSNE类 中借鉴了一些东西。
首先,我们将导入以下库并设置一些绘图属性,这些属性将在我们绘制数据时发挥作用。
import numpy as np
from sklearn.datasets import load_digits
from scipy.spatial.distance import pdist
from sklearn.manifold.t_sne import _joint_probabilities
from scipy import linalg
from sklearn.metrics import pairwise_distances
from scipy.spatial.distance import squareform
from sklearn.manifold import TSNE
from matplotlib import pyplot as plt
import seaborn as sns
sns.set(rc={'figure.figsize':(11.7,8.27)})
palette = sns.color_palette("bright", 10)在此示例中,我们将使用手写数字数据。scikit-learn库提供了一种将它们导入我们程序的方法。
X, y = load_digits(return_X_y=True)人能够理解或者可见的最多维度是3,所以这里为t-SNE选择2或3作为组件数(也就是聚类数量)。另一方面,perplexity与算法中使用的最近邻居的数量有关。不同的perplexity可能会导致最终结果发生巨大变化。在我们的情况下,我们将其设置为scitkit-learn默认值t-SNE(30)的实现。注:根据numpy文档,机器精度(epsilon)是最小的可表示正数,因此1.0 + eps != 1.0。换句话说,由于缺少必要的位,因此计算机无法操纵机器精度(epsilon)以下的任何数字。正如我们将看到的,使用np.maximum检查矩阵中的值是否小于机器的epsilon并在出现时替换它们。
MACHINE_EPSILON = np.finfo(np.double).eps
n_components = 2
perplexity = 30接下来,我们定义fit功能。我们调用fit做数据转换。
def fit(X):
n_samples = X.shape[0]
# Compute euclidean distance
distances = pairwise_distances(X, metric='euclidean', squared=True)
# Compute joint probabilities p_ij from distances.
P = _joint_probabilities(distances=distances, desired_perplexity=perplexity, verbose=False)
# The embedding is initialized with iid samples from Gaussians with standard deviation 1e-4.
X_embedded = 1e-4 * np.random.mtrand._rand.randn(n_samples, n_components).astype(np.float32)
# degrees_of_freedom = n_components - 1 comes from
# "Learning a Parametric Embedding by Preserving Local Structure"
# Laurens van der Maaten, 2009.
degrees_of_freedom = max(n_components - 1, 1)
return _tsne(P, degrees_of_freedom, n_samples, X_embedded=X_embedded)
fit函数实现了很多功能,下面分解介绍。
1.将样本数存储在变量中,以便后续使用。
2.计算每个数据点之间的欧式距离。这对应于||xi — xj||^2。

3.将上一步中计算出的欧几里德距离作为参数传递给_join_probabilities函数,然后计算并返回一个矩阵p_ji(使用相同的方程式)。
4.使用标准差为1e-4的高斯分布随机选择值来创建缩减特征空间。
5.定义degrees_of_freedom。源代码中有一条注释, 在这篇论文中有解释他们推理过程。基本上,从经验上可以看出,当将degrees_of_freedom设置为组件数减去一个时,我们会得到更好的结果(粗体)。
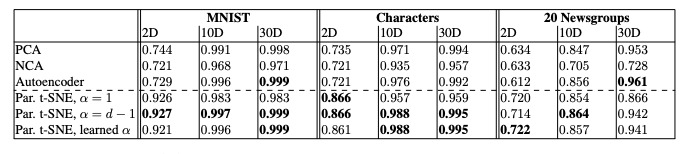
6.最后,我们调用tsne函数,该函数的实现如下。
def _tsne(P, degrees_of_freedom, n_samples, X_embedded):
params = X_embedded.ravel()
obj_func = _kl_divergence
params = _gradient_descent(obj_func, params, [P, degrees_of_freedom, n_samples, n_components])
X_embedded = params.reshape(n_samples, n_components)
return X_embedded
此函数实际上没有太多内容。首先,我们使用np.ravel将向量展平为一维数组。
>>> x = np.array([[1, 2, 3], [4, 5, 6]])
>>> np.ravel(x)
array([1, 2, 3, 4, 5, 6])然后我们使用梯度下降来最小化KL散度。完成后,我们将嵌入更改回2D数组并返回它。
接下来,看看计算细节。以下代码块负责基于kl发散和梯度计算误差。
def _kl_divergence(params, P, degrees_of_freedom, n_samples, n_components):
X_embedded = params.reshape(n_samples, n_components)dist = pdist(X_embedded, “sqeuclidean”)
dist /= degrees_of_freedom
dist += 1.
dist **= (degrees_of_freedom + 1.0) / -2.0
Q = np.maximum(dist / (2.0 * np.sum(dist)), MACHINE_EPSILON)
# Kullback-Leibler divergence of P and Q
kl_divergence = 2.0 * np.dot(P, np.log(np.maximum(P, MACHINE_EPSILON) / Q))
# Gradient: dC/dY
grad = np.ndarray((n_samples, n_components), dtype=params.dtype)
PQd = squareform((P – Q) * dist)
for i in range(n_samples):
grad[i] = np.dot(np.ravel(PQd[i], order=’K’), X_embedded[i] – X_embedded)
grad = grad.ravel()
c = 2.0 * (degrees_of_freedom + 1.0) / degrees_of_freedom
grad *= c
return kl_divergence, grad
同样,让我们一步一步地讲解代码。
1.第一部分计算低维映射中各点的概率分布。
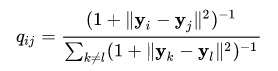
实际上使用的是上面方程式的变体,其中包括自由度。
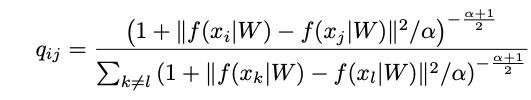
其中α表示Student-t分布的自由度数
2.计算KL散度(np.dot)。

3.计算梯度(偏导数)。dist实际上是yi — yj:
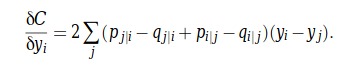
同样,他们使用自由度以上方程的变化形式。

其中α表示Student-t分布的自由度数
梯度下降函数通过最小化KL散度来更新嵌入中的值。当梯度范数低于阈值或达到最大迭代次数而没有任何进展时,我们提前停止。
def _gradient_descent(obj_func, p0, args, it=0, n_iter=1000, n_iter_check=1, n_iter_without_progress=300, momentum=0.8, learning_rate=200.0, min_gain=0.01, min_grad_norm=1e-7): p = p0.copy().ravel() update = np.zeros_like(p) gains = np.ones_like(p) error = np.finfo(np.float).max best_error = np.finfo(np.float).max best_iter = i = it for i in range(it, n_iter): error, grad = obj_func(p, *args) grad_norm = linalg.norm(grad) inc = update * grad < 0.0 dec = np.invert(inc) gains[inc] += 0.2 gains[dec] *= 0.8 np.clip(gains, min_gain, np.inf, out=gains) grad *= gains update = momentum * update - learning_rate * grad p += updateprint("[t-SNE] Iteration %d: error = %.7f," " gradient norm = %.7f" % (i + 1, error, grad_norm)) if error < best_error: best_error = error best_iter = i elif i - best_iter > n_iter_without_progress: break if grad_norm <= min_grad_norm: break return p
到这里,已经做好了在数据上执行fit了。
X_embedded = fit(X)如我们所见,该模型在根据像素位置分离不同数字方面表现很好。
sns.scatterplot(X_embedded[:,0], X_embedded[:,1], hue=y, legend='full', palette=palette)
t-SNE的Sklearn代码
下面是scikit-learn的t-SNE实现。
tsne = TSNE()
X_embedded = tsne.fit_transform(X)如我们所见,该模型成功地获取了64维数据集,并将其投影到2维空间中,从而使相似的样本聚在一起。
sns.scatterplot(X_embedded[:,0], X_embedded[:,1], hue=y, legend='full', palette=palette)
