我覺得我屬於比較笨的那一類人。當理解一個抽象/數學的想法時,我必須真正把它放在圖像中,必須在頭腦中看到並觸摸它。我需要通過幾何物體,想法背後的直覺,或者更好的現實生活中的生動隱喻,才能更好地理解這些概念。
有時候,當我發現人們沒有想到或者至少不用這種方式解釋事情時,隻是指著方程式和論文,說:“沒有簡單的解釋”,我會很生氣。往往在經過思考之後,我可以找到那些想法的直觀解釋。昨天當我試圖理解應用於機器學習的L1正則化時,就有一次這樣的經曆。因此,我想製作這個愚蠢而直觀的作品,以便即使麵對普通的路人甲也可以解釋清楚這個想法。
在小型數據集上執行機器學習任務時,常常會遇到過擬合問題,因為模型可準確記住所有訓練數據,包括噪音和不相關的特征。這種模型通常在新的測試或以前從未見過的真實數據上表現不佳。因為模型對待訓練數據過於嚴肅,所以沒有從中學習到真正有意義的模式,隻是記住它所看到的一切。
現在,解決此問題的一種解決方案稱為正規化。這個想法是將L1範數應用於機器學習問題的解決方案向量(在深度學習的情況下,它是神經網絡的權重),並使其盡可能小。因此,如果您的初始目標是找到最佳向量x來最小化損失函數f(x),那麽您的新任務應將x的L1範數納入公式中,找到最小值(f(x)+ L1norm(x))。經常有這樣的斷言:具有小L1範數的x往往是一個稀疏解。稀疏意味著x的大部分組件(權重)是零,隻有少數是非零的。而一個稀疏的解決方案可以避免過擬合。
就是這樣,這就是在大多數文章,教科書和材料中的解釋。給一個沒有任何解釋的觀點感覺就像在我的腦後部戳來一支矛。
不確定大家是什麽感受,但使用L1標準來確保稀疏並因此避免過擬合的原因對我來說並不那麽明顯。我花了一些時間來弄清楚為什麽。總結起來,有這些問題:
- 為什麽一個小的L1規範給出了一個稀疏的解決方案?
- 為什麽稀疏解決方案能避免過擬合?
- 為什麽正規化確實可以起作用?
我最初的困惑來自於我隻看L1的規範,並且隻考慮L1規範的小意味著什麽。然而,我應該做的是考慮將損失函數和L1範數懲罰作為一個整體。
讓我們從一開始就解釋過擬合的問題。我想用一個具體的例子。假設你購買了一個機器人,並且想通過查看以下示例教他對中文字符進行分類:

前5個字符屬於第一類,後5個屬於第二類。這10個字符是您擁有的唯一訓練數據。

機器人有足夠大的內存來記住5個字符。看到所有10個字符後,機器人學會了一種分類方法:它精確記住所有前5個字符。隻要角色不是這5個角色中的一員,機器人就會將角色放入第二類。
當然,這種方法在10個訓練角色上會很好地工作,因為機器人可以達到100%的準確度。但是,如果提供了一個新字符:

這個字符應該屬於第一類。但是因為它從來沒有出現在訓練數據中,所以機器人從未見過它。基於它的算法,機器人會將這個角色放到第二個類別中,但顯然這是錯誤的。

對於我們人來說,看到這個模式應該是非常明顯的。屬於第一類的所有字符都具有相同的部分。機器人不能完成任務,因為它聰明過頭,訓練數據太小。
這是過擬合的問題。但是什麽是正規化,為什麽稀疏可以避免過擬合?

現在假設你對你的機器人生氣了。你用錘子敲擊機器人的頭部,在做這件事的時候,你把它的一些內存芯片從頭上搖下來。你基本上已經讓機器人變成了笨蛋。現在,機器人隻能記住一個字符部分,而不能記住5個字符。
您讓機器人通過查看全部10個字符再次進行訓練,並仍然強製他達到相同的精度。因為這次他不記得所有5個角色,所以你基本上迫使他尋找一個更簡單的模式。現在他發現了所有A類角色的共同部分!
這正是L1規範正則化所做的。它在您的機器(型號)上觸發,使其成為“dumber”。所以不是簡單地記住東西,而是從數據中尋找更簡單的模式。在機器人的情況下,當他能夠記住5個字符時,他的“大腦”具有5的矢量:[把,打,扒,捕,拉]。現在經過正規化(打擊)後,他的記憶中 的4個插槽變得無法使用。因此,新學習的矢量是:[扌,0,0,0,0],很明顯,這是一個稀疏矢量。
更正式地說,當你用較少的訓練數據求解大向量x時。 x的解決方案可能很多。
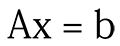
這裏A是包含所有訓練數據的矩陣。 x是您正在尋找的解決方案向量。 b是標簽矢量。
如果數據不夠,並且模型的參數大小很大,則矩陣A不會足夠“tall”,並且x很長。所以上麵的等式看起來像這樣:
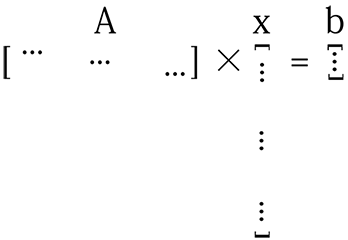
對於這樣的係統,x的解決方案可能是無限的。要從這些解決方案中找到一個好的解決方案,您需要確保所選解決方案x的每個組件都能捕獲數據的有用功能。通過L1正則化,實質上使得向量x更小(稀疏),因為其大部分組件都是無用的(零),同時,剩餘的非零組件是非常“有用的”。
我能想到的另一個比喻是:假設你是一個國家的國王,人口眾多,總體GDP還不錯,但人均收入很低。你的每一個公民都很懶惰,沒有生產力,你很生氣。因此,你的命令是“富有成效,堅強和努力工作,否則就完蛋!”並且你執行與以前相同的GDP。結果,許多人由於你的苛刻而死亡,那些從你的暴政中幸存下來的人變得非常有能力和生產力。你可以認為這裏的人口是你的解決方案向量x的大小,並命令人們生產或死亡本質上是正規化。在正則化稀疏解決方案中,確保向量x的每個分量都非常有效。每個組件都必須捕獲一些有用的功能或數據模式。
深度學習的另一種正規化方式是dropout。這個想法很簡單,從神經網絡中刪除一些隨機的神經連接,同時訓練並在一段時間後重新添加它們。從本質上講,這仍然試圖通過減少神經網絡的大小來製作模型“dumber”,並將更多的責任和壓力放在剩餘的權重上來學習一些有用的東西。一旦這些權重學習了好的功能,然後添加其他連接以接受新數據。我想把這個加回去的東西當作“在你短暫的時候把移民介紹給你的王國”這個比喻。
基於這個“making model dumber”的想法,我想我們可以想出其他類似的方法來避免過擬合,例如從一個小型網絡開始,並在有更多數據可用時逐漸向網絡添加新的神經元和連接。或者在訓練時進行修剪以消除接近於零的連接。
到目前為止,我們已經證明為什麽稀疏可以避免過擬合。但是,為什麽將L1範數添加到損失函數並迫使解的L1範數很小會產生稀疏性?
昨天當我第一次想到這個時,我使用了兩個示例向量[0.1,0.1]和[1000,0]。第一個向量顯然不稀疏,但它具有較小的L1範數。這就是為什麽我很困惑,因為單看L1準則不會讓這個想法變得可以理解。我必須考慮整個損失函數。
讓我們回到Ax = b的問題,用一個簡單而具體的例子。假設我們想要找到與2D空間中的一組點相匹配的線。我們都知道你需要至少2個點才能確定一條線。但是如果訓練數據隻有一點呢?那麽你將有無限的解決方案:通過這一點的每條線都是一個解決方案。假設該點在[10,5],並且一條線被定義為函數y = a * x + b。然後問題是找到這個方程的解決方案:
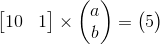
由於b = 5 – 10 * a,所以下麵這行b = 5 – 10 * a上的所有點應該是一個解決方案:
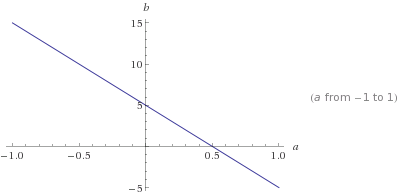
但是如何找到L1規範中的稀疏分支?
L1範數被定義為向量的所有分量的絕對值的總和。例如,如果一個向量是[x,y],那麽它的L1範數是| x | + | y |。
現在,如果我們畫出L1範數等於常數c的所有點,那麽這些點應該形成如下的東西(紅色):

這個形狀看起來像一個傾斜的正方形。在高維空間中,它將是一個八麵體。注意在這個紅色的形狀上,並不是所有的點都是稀疏的。隻有在尖點,點是稀疏的。也就是說,一個點的x或y分量是零。現在找到稀疏解決方案的方法是通過將不斷增長的c提供給“touch”藍色求解線,從原點放大該紅色形狀。直覺是觸摸點最有可能在形狀的一端。由於尖端是一個稀疏點,觸點定義的解決方案也是一個稀疏解決方案。
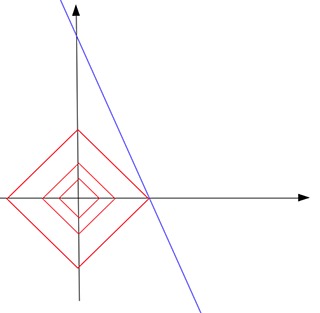
例如,在該圖中,紅色形狀增長了3倍,直到它接觸到藍色線b = 5-10 * a。如您所見,觸點位於紅色形狀的尖端。觸點[0.5,0]是一個稀疏矢量。因此,我們說,通過在所有可能的解決方案(藍線上的點)中找到具有最小L1範數(0.5)的解點,我們找到了一個針對我們的問題的稀疏解[0.5,0]。在接觸點上,常數c是所有可能解決方案中可以找到的最小L1範數。
使用L1範數的直覺是由L1範數等於常數c的所有點形成的形狀有許多碰巧稀疏的尖(尖峰)(位於坐標係的一個軸上)。現在我們擴展這種形狀以觸及為問題找到的解決方案(通常是高維的麵或cross-section)。 2個形狀的觸點位於L1標準形狀的“tips”或“spikes”之一的概率非常高。這就是為什麽要將L1範數放入損失函數公式中,以便您可以繼續尋找具有更小c的解(在L1範數的“sparse”尖端)。 (所以在實際損失函數的情況下,你實質上是縮小了紅色的形狀以找到一個觸點,而不是從原點擴大它。)
L1範數是否總能觸碰解決方案並找到我們一個稀疏的解決方案?不一定。假設我們仍然想從2D點中找出一條線,但是這一次,唯一的訓練數據是一個點[1,1000]。在這種情況下,解線b = 1000-a平行於L1範數形狀的其中一條邊:
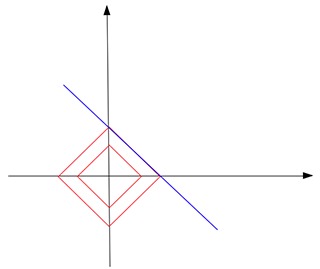
最終,它們觸及邊,而不是尖端。不僅這次你不能有獨特的解決方案,你的大多數正則化解決方案仍然不是稀疏的(除了兩個尖點)。
但是,再次碰觸尖端的可能性非常高。我想這對於高維,真實世界的問題更是如此。當你的坐標係有更多的軸時,你的L1標準形狀應該有更多的尖峰或尖端。它必須看起來像仙人掌或刺蝟!我無法想象。


如果你將一個人推向仙人掌,他被刺針刺的可能性非常高。這也是他們發明這種變形武器的原因,這也是他們為什麽要使用L1標準的原因。

但是L1標準是尋找稀疏解決方案的最佳標準嗎?那麽,事實證明,0 <= p <=1時的Lp規範可以給出最佳結果。
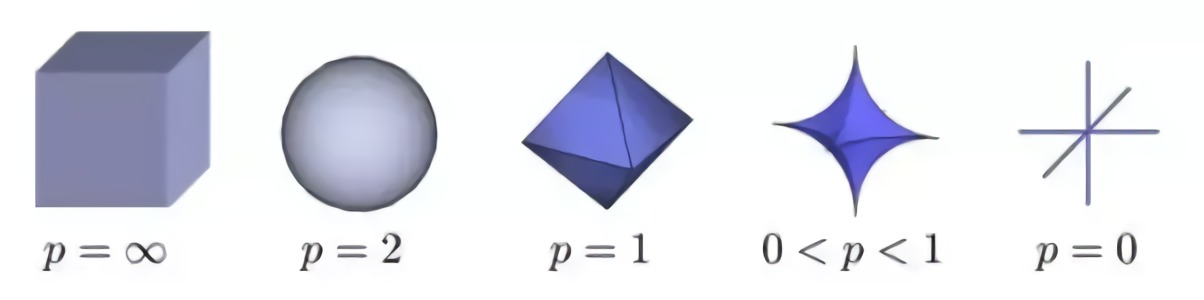
正如你所看到的那樣,當p <1時,形狀更“可怕”,更尖銳,突發尖峰。而當p = 2時,形狀變成平滑無害的球。那為什麽不讓p <1呢?那是因為當p <1時,有計算困難。
總之,過擬合是與您的可用訓練數據相比較時機器學習模型太大(參數太多)出現的問題。在這種情況下,模型傾向於記住包括嘈雜在內的所有訓練案例以獲得更好的訓練分數。為了避免這種情況,正則化應用於模型以(實質上)減小其大小。正則化的一種方法是確保訓練好的模型是稀疏的,這樣它的大部分組件都是零。這些零點基本上是無用的,而且你的模型尺寸實際上減小了。
使用L1範數尋找稀疏解的原因是由於其特殊的形狀。它的尖峰恰好處於稀疏點。使用它接觸解決方案的表麵很可能會在尖端找到接觸點,從而形成稀疏的解決方案。
想想這個:

當僵屍爆發時,哪一個應該成為首選的武器?

