我觉得我属于比较笨的那一类人。当理解一个抽象/数学的想法时,我必须真正把它放在图像中,必须在头脑中看到并触摸它。我需要通过几何物体,想法背后的直觉,或者更好的现实生活中的生动隐喻,才能更好地理解这些概念。
有时候,当我发现人们没有想到或者至少不用这种方式解释事情时,只是指着方程式和论文,说:“没有简单的解释”,我会很生气。往往在经过思考之后,我可以找到那些想法的直观解释。昨天当我试图理解应用于机器学习的L1正则化时,就有一次这样的经历。因此,我想制作这个愚蠢而直观的作品,以便即使面对普通的路人甲也可以解释清楚这个想法。
在小型数据集上执行机器学习任务时,常常会遇到过拟合问题,因为模型可准确记住所有训练数据,包括噪音和不相关的特征。这种模型通常在新的测试或以前从未见过的真实数据上表现不佳。因为模型对待训练数据过于严肃,所以没有从中学习到真正有意义的模式,只是记住它所看到的一切。
现在,解决此问题的一种解决方案称为正规化。这个想法是将L1范数应用于机器学习问题的解决方案向量(在深度学习的情况下,它是神经网络的权重),并使其尽可能小。因此,如果您的初始目标是找到最佳向量x来最小化损失函数f(x),那么您的新任务应将x的L1范数纳入公式中,找到最小值(f(x)+ L1norm(x))。经常有这样的断言:具有小L1范数的x往往是一个稀疏解。稀疏意味着x的大部分组件(权重)是零,只有少数是非零的。而一个稀疏的解决方案可以避免过拟合。
就是这样,这就是在大多数文章,教科书和材料中的解释。给一个没有任何解释的观点感觉就像在我的脑后部戳来一支矛。
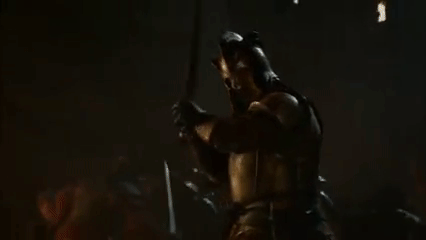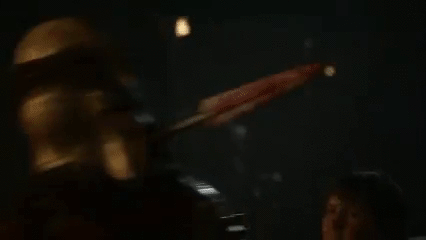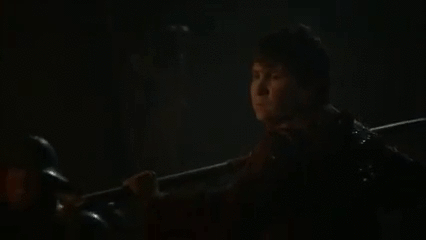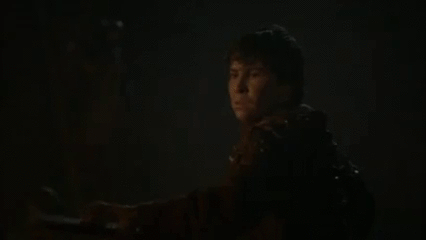
不确定大家是什么感受,但使用L1标准来确保稀疏并因此避免过拟合的原因对我来说并不那么明显。我花了一些时间来弄清楚为什么。总结起来,有这些问题:
- 为什么一个小的L1规范给出了一个稀疏的解决方案?
- 为什么稀疏解决方案能避免过拟合?
- 为什么正规化确实可以起作用?
我最初的困惑来自于我只看L1的规范,并且只考虑L1规范的小意味着什么。然而,我应该做的是考虑将损失函数和L1范数惩罚作为一个整体。
让我们从一开始就解释过拟合的问题。我想用一个具体的例子。假设你购买了一个机器人,并且想通过查看以下示例教他对中文字符进行分类:

前5个字符属于第一类,后5个属于第二类。这10个字符是您拥有的唯一训练数据。

机器人有足够大的内存来记住5个字符。看到所有10个字符后,机器人学会了一种分类方法:它精确记住所有前5个字符。只要角色不是这5个角色中的一员,机器人就会将角色放入第二类。
当然,这种方法在10个训练角色上会很好地工作,因为机器人可以达到100%的准确度。但是,如果提供了一个新字符:

这个字符应该属于第一类。但是因为它从来没有出现在训练数据中,所以机器人从未见过它。基于它的算法,机器人会将这个角色放到第二个类别中,但显然这是错误的。

对于我们人来说,看到这个模式应该是非常明显的。属于第一类的所有字符都具有相同的部分。机器人不能完成任务,因为它聪明过头,训练数据太小。
这是过拟合的问题。但是什么是正规化,为什么稀疏可以避免过拟合?

现在假设你对你的机器人生气了。你用锤子敲击机器人的头部,在做这件事的时候,你把它的一些内存芯片从头上摇下来。你基本上已经让机器人变成了笨蛋。现在,机器人只能记住一个字符部分,而不能记住5个字符。
您让机器人通过查看全部10个字符再次进行训练,并仍然强制他达到相同的精度。因为这次他不记得所有5个角色,所以你基本上迫使他寻找一个更简单的模式。现在他发现了所有A类角色的共同部分!
这正是L1规范正则化所做的。它在您的机器(型号)上触发,使其成为“dumber”。所以不是简单地记住东西,而是从数据中寻找更简单的模式。在机器人的情况下,当他能够记住5个字符时,他的“大脑”具有5的矢量:[把,打,扒,捕,拉]。现在经过正规化(打击)后,他的记忆中 的4个插槽变得无法使用。因此,新学习的矢量是:[扌,0,0,0,0],很明显,这是一个稀疏矢量。
更正式地说,当你用较少的训练数据求解大向量x时。 x的解决方案可能很多。
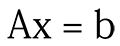
这里A是包含所有训练数据的矩阵。 x是您正在寻找的解决方案向量。 b是标签矢量。
如果数据不够,并且模型的参数大小很大,则矩阵A不会足够“tall”,并且x很长。所以上面的等式看起来像这样:
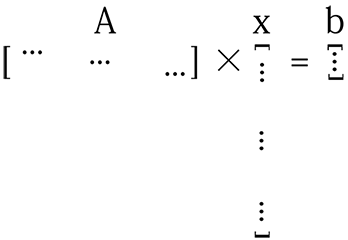
对于这样的系统,x的解决方案可能是无限的。要从这些解决方案中找到一个好的解决方案,您需要确保所选解决方案x的每个组件都能捕获数据的有用功能。通过L1正则化,实质上使得向量x更小(稀疏),因为其大部分组件都是无用的(零),同时,剩余的非零组件是非常“有用的”。
我能想到的另一个比喻是:假设你是一个国家的国王,人口众多,总体GDP还不错,但人均收入很低。你的每一个公民都很懒惰,没有生产力,你很生气。因此,你的命令是“富有成效,坚强和努力工作,否则就完蛋!”并且你执行与以前相同的GDP。结果,许多人由于你的苛刻而死亡,那些从你的暴政中幸存下来的人变得非常有能力和生产力。你可以认为这里的人口是你的解决方案向量x的大小,并命令人们生产或死亡本质上是正规化。在正则化稀疏解决方案中,确保向量x的每个分量都非常有效。每个组件都必须捕获一些有用的功能或数据模式。
深度学习的另一种正规化方式是dropout。这个想法很简单,从神经网络中删除一些随机的神经连接,同时训练并在一段时间后重新添加它们。从本质上讲,这仍然试图通过减少神经网络的大小来制作模型“dumber”,并将更多的责任和压力放在剩余的权重上来学习一些有用的东西。一旦这些权重学习了好的功能,然后添加其他连接以接受新数据。我想把这个加回去的东西当作“在你短暂的时候把移民介绍给你的王国”这个比喻。
基于这个“making model dumber”的想法,我想我们可以想出其他类似的方法来避免过拟合,例如从一个小型网络开始,并在有更多数据可用时逐渐向网络添加新的神经元和连接。或者在训练时进行修剪以消除接近于零的连接。
到目前为止,我们已经证明为什么稀疏可以避免过拟合。但是,为什么将L1范数添加到损失函数并迫使解的L1范数很小会产生稀疏性?
昨天当我第一次想到这个时,我使用了两个示例向量[0.1,0.1]和[1000,0]。第一个向量显然不稀疏,但它具有较小的L1范数。这就是为什么我很困惑,因为单看L1准则不会让这个想法变得可以理解。我必须考虑整个损失函数。
让我们回到Ax = b的问题,用一个简单而具体的例子。假设我们想要找到与2D空间中的一组点相匹配的线。我们都知道你需要至少2个点才能确定一条线。但是如果训练数据只有一点呢?那么你将有无限的解决方案:通过这一点的每条线都是一个解决方案。假设该点在[10,5],并且一条线被定义为函数y = a * x + b。然后问题是找到这个方程的解决方案:
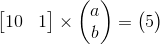
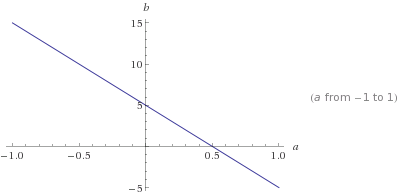
由于b = 5 – 10 * a,所以下面这行b = 5 – 10 * a上的所有点应该是一个解决方案:
但是如何找到L1规范中的稀疏分支?
L1范数被定义为向量的所有分量的绝对值的总和。例如,如果一个向量是[x,y],那么它的L1范数是| x | + | y |。
现在,如果我们画出L1范数等于常数c的所有点,那么这些点应该形成如下的东西(红色):

这个形状看起来像一个倾斜的正方形。在高维空间中,它将是一个八面体。注意在这个红色的形状上,并不是所有的点都是稀疏的。只有在尖点,点是稀疏的。也就是说,一个点的x或y分量是零。现在找到稀疏解决方案的方法是通过将不断增长的c提供给“touch”蓝色求解线,从原点放大该红色形状。直觉是触摸点最有可能在形状的一端。由于尖端是一个稀疏点,触点定义的解决方案也是一个稀疏解决方案。
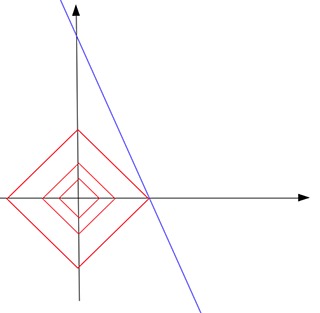
例如,在该图中,红色形状增长了3倍,直到它接触到蓝色线b = 5-10 * a。如您所见,触点位于红色形状的尖端。触点[0.5,0]是一个稀疏矢量。因此,我们说,通过在所有可能的解决方案(蓝线上的点)中找到具有最小L1范数(0.5)的解点,我们找到了一个针对我们的问题的稀疏解[0.5,0]。在接触点上,常数c是所有可能解决方案中可以找到的最小L1范数。
使用L1范数的直觉是由L1范数等于常数c的所有点形成的形状有许多碰巧稀疏的尖(尖峰)(位于坐标系的一个轴上)。现在我们扩展这种形状以触及为问题找到的解决方案(通常是高维的面或cross-section)。 2个形状的触点位于L1标准形状的“tips”或“spikes”之一的概率非常高。这就是为什么要将L1范数放入损失函数公式中,以便您可以继续寻找具有更小c的解(在L1范数的“sparse”尖端)。 (所以在实际损失函数的情况下,你实质上是缩小了红色的形状以找到一个触点,而不是从原点扩大它。)
L1范数是否总能触碰解决方案并找到我们一个稀疏的解决方案?不一定。假设我们仍然想从2D点中找出一条线,但是这一次,唯一的训练数据是一个点[1,1000]。在这种情况下,解线b = 1000-a平行于L1范数形状的其中一条边:
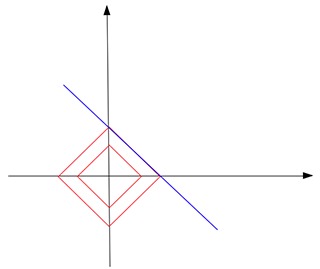
最终,它们触及边,而不是尖端。不仅这次你不能有独特的解决方案,你的大多数正则化解决方案仍然不是稀疏的(除了两个尖点)。
但是,再次碰触尖端的可能性非常高。我想这对于高维,真实世界的问题更是如此。当你的坐标系有更多的轴时,你的L1标准形状应该有更多的尖峰或尖端。它必须看起来像仙人掌或刺猬!我无法想象。


如果你将一个人推向仙人掌,他被刺针刺的可能性非常高。这也是他们发明这种变形武器的原因,这也是他们为什么要使用L1标准的原因。

但是L1标准是寻找稀疏解决方案的最佳标准吗?那么,事实证明,0 <= p <=1时的Lp规范可以给出最佳结果。
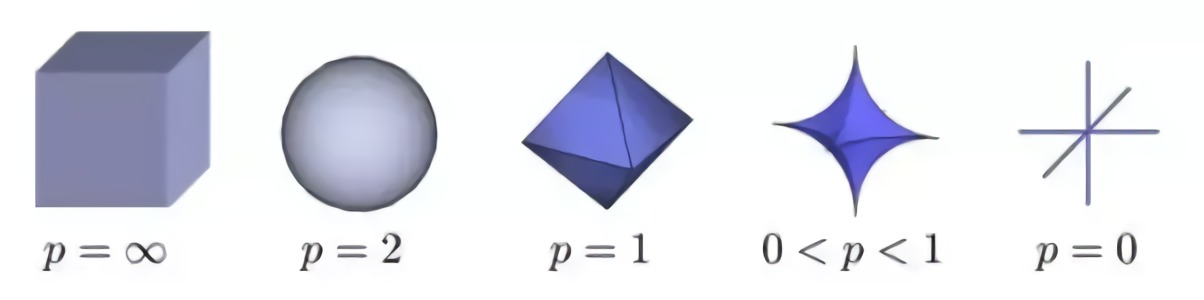
正如你所看到的那样,当p <1时,形状更“可怕”,更尖锐,突发尖峰。而当p = 2时,形状变成平滑无害的球。那为什么不让p <1呢?那是因为当p <1时,有计算困难。
总之,过拟合是与您的可用训练数据相比较时机器学习模型太大(参数太多)出现的问题。在这种情况下,模型倾向于记住包括嘈杂在内的所有训练案例以获得更好的训练分数。为了避免这种情况,正则化应用于模型以(实质上)减小其大小。正则化的一种方法是确保训练好的模型是稀疏的,这样它的大部分组件都是零。这些零点基本上是无用的,而且你的模型尺寸实际上减小了。
使用L1范数寻找稀疏解的原因是由于其特殊的形状。它的尖峰恰好处于稀疏点。使用它接触解决方案的表面很可能会在尖端找到接触点,从而形成稀疏的解决方案。
想想这个:

当僵尸爆发时,哪一个应该成为首选的武器?

