R recipes step_harmonic 添加正弦和余弦项以进行谐波分析

step_harmonic(
  recipe,
  ...,
  role = "predictor",
  trained = FALSE,
  frequency = NA_real_,
  cycle_size = NA_real_,
  starting_val = NA_real_,
  keep_original_cols = FALSE,
  columns = NULL,
  skip = FALSE,
  id = rand_id("harmonic")
)

A_j cos(\sigma_j t_i - \Phi_j) = C_j cos(\sigma_j t_i) + S_j sin(\sigma_j t_i)

A_j = \sqrt{C^2_j + S^2_j}

\Phi_j = \arctan{(S_j / C_j)}

其他单独的转换步骤：step_BoxCox() , step_YeoJohnson() , step_bs() , step_hyperbolic() , step_inverse() , step_invlogit() , step_logit() , step_log() , step_mutate() , step_ns() , step_percentile() , step_poly() , step_relu() , step_sqrt()

library(ggplot2, quietly = TRUE)
library(dplyr)

data(sunspot.year)
sunspots <-
  tibble(
    year = 1700:1988,
    n_sunspot = sunspot.year,
    type = "measured"
  ) %>%
  slice(1:75)

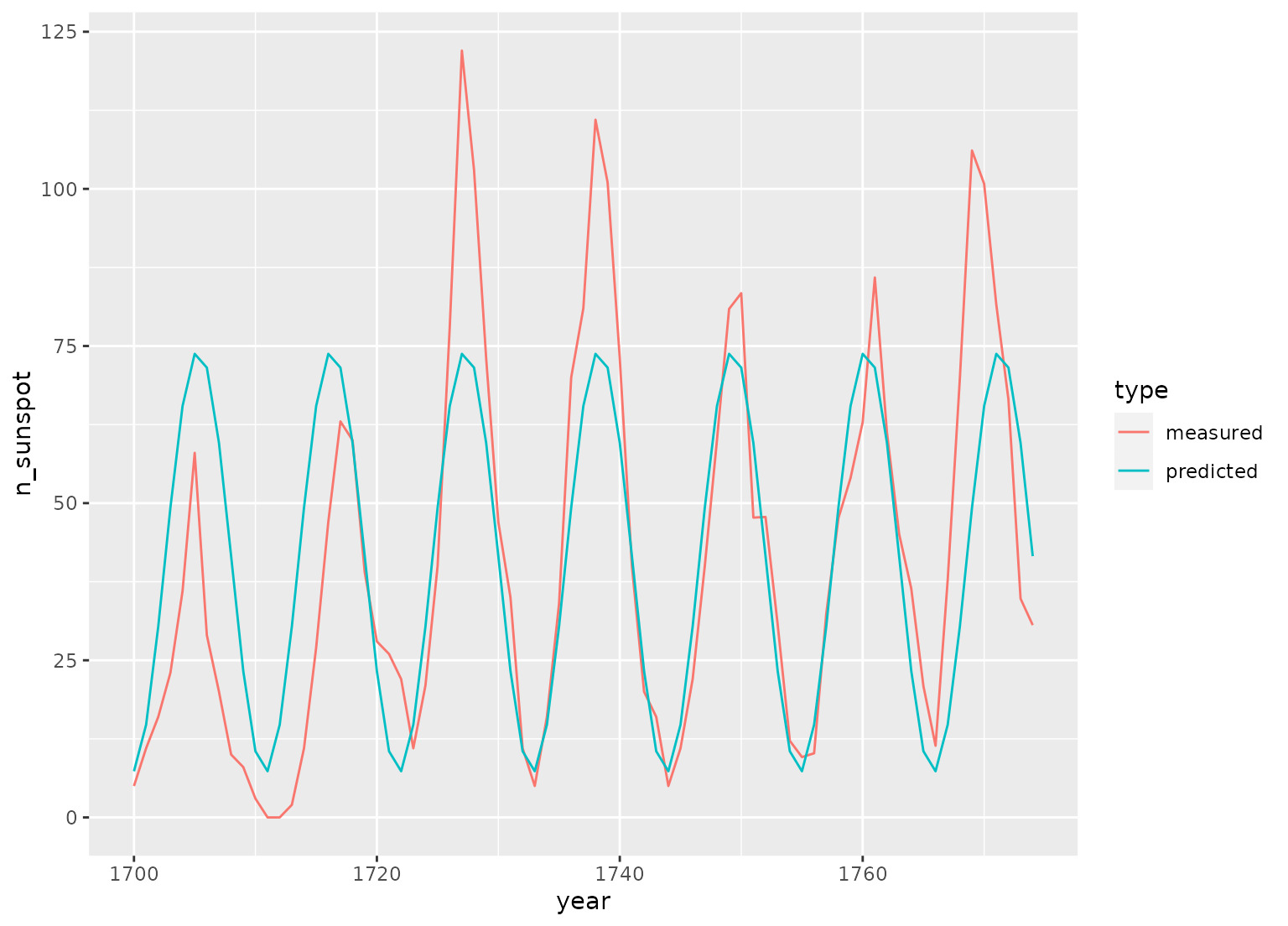
# sunspots period is around 11 years, sample spacing is one year
dat <- recipe(n_sunspot ~ year, data = sunspots) %>%
  step_harmonic(year, frequency = 1 / 11, cycle_size = 1) %>%
  prep() %>%
  bake(new_data = NULL)

fit <- lm(n_sunspot ~ year_sin_1 + year_cos_1, data = dat)

preds <- tibble(
  year = sunspots$year,
  n_sunspot = fit$fitted.values,
  type = "predicted"
)

bind_rows(sunspots, preds) %>%
  ggplot(aes(x = year, y = n_sunspot, color = type)) +
  geom_line()



# ------------------------------------------------------------------------------
# POSIXct example

date_time <-
  as.POSIXct(
    paste0(rep(1959:1997, each = 12), "-", rep(1:12, length(1959:1997)), "-01"),
    tz = "UTC"
  )

carbon_dioxide <- tibble(
  date_time = date_time,
  co2 = as.numeric(co2),
  type = "measured"
)

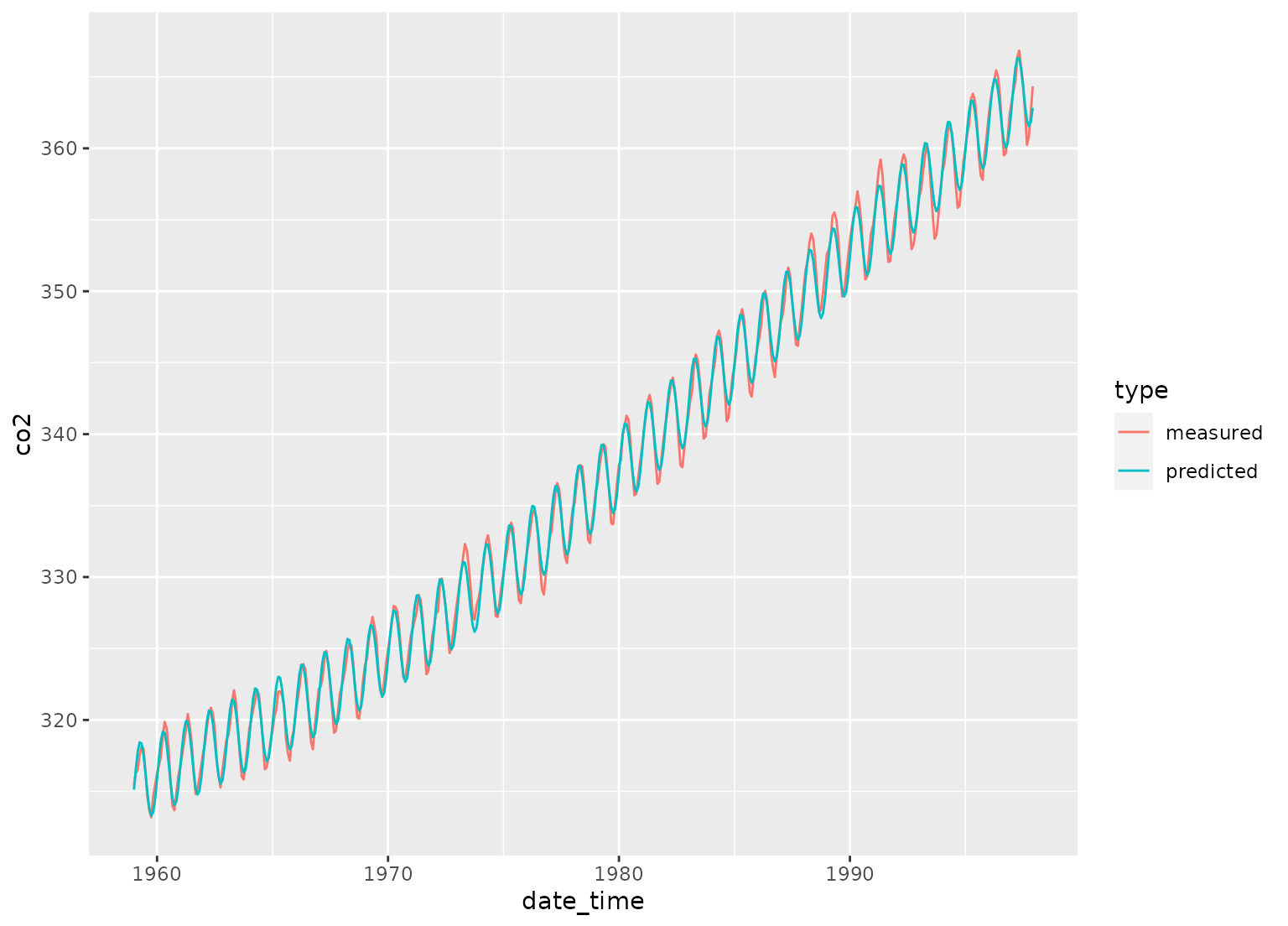
# yearly co2 fluctuations
dat <-
  recipe(co2 ~ date_time,
    data = carbon_dioxide
  ) %>%
  step_mutate(date_time_num = as.numeric(date_time)) %>%
  step_ns(date_time_num, deg_free = 3) %>%
  step_harmonic(date_time, frequency = 1, cycle_size = 86400 * 365.24) %>%
  prep() %>%
  bake(new_data = NULL)

fit <- lm(co2 ~ date_time_num_ns_1 + date_time_num_ns_2 +
  date_time_num_ns_3 + date_time_sin_1 +
  date_time_cos_1, data = dat)

preds <- tibble(
  date_time = date_time,
  co2 = fit$fitted.values,
  type = "predicted"
)

bind_rows(carbon_dioxide, preds) %>%
  ggplot(aes(x = date_time, y = co2, color = type)) +
  geom_line()