Java Bloom Filter用法及代码示例

布隆过滤器用于确定元素是否存在于集合中的集合成员资格set或不。布隆过滤器的发明者伯顿·H·布鲁姆1970 年，在一篇名为允许错误的哈希编码中的空间/时间Trade-offs (1970)。布隆过滤器是一种概率数据结构，适用于hash-coding方法(如同HashTable)。

我们什么时候需要布隆过滤器？
考虑以下任一情况：

假设我们有一个包含一些元素的列表，并且我们想检查给定元素是否存在？
考虑您正在开发电子邮件服务，并且您正在尝试使用给定用户名已经存在或不存在的函数来实现注册端点？
假设您给出了一组列入黑名单的 IP，并且您想过滤掉给定的 IP 是否属于黑名单？

如果没有布隆过滤器的帮助，这些问题可以解决吗？

让我们尝试使用HashSet来解决这些问题


import java.util.HashSet; 
import java.util.Set; 
  
public class SetDemo { 
    public static void main(String[] args) 
    { 
        Set<String> blackListedIPs 
            = new HashSet<>(); 
        blackListedIPs.add("192.170.0.1"); 
        blackListedIPs.add("75.245.10.1"); 
        blackListedIPs.add("10.125.22.20"); 
  
        // true 
        System.out.println( 
            blackListedIPs 
                .contains( 
                    "75.245.10.1")); 
  
        // false 
        System.out.println( 
            blackListedIPs 
                .contains( 
                    "101.125.20.22")); 
    } 
}

输出：

true
false

为什么像HashSet或HashTable这样的数据结构会失败？
当我们的数据集有限时，HashSet 或 HashTable 效果很好，但当我们处理大量数据集时，可能不适合。对于大数据集，需要大量时间和大量内存。

数据集大小与 HashSet 等数据结构的插入时间

----------------------------------------------
|Number of UUIDs          Insertion Time(ms) |
----------------------------------------------
|10                         <1               |
|100                         3               |
|1, 000                      58              |
|10, 000                     122             |
|100, 000                    836             |
|1, 000, 000                 7395            |
----------------------------------------------

数据集大小与 HashSet 等数据结构的 memory (JVM Heap)

----------------------------------------------
|Number of UUIDs            JVM heap used(MB) |
----------------------------------------------
|10                         <2                |   
|100                        <2                |
|1, 000                      3                |
|10, 000                     9                |
|100, 000                    37               |
|1, 000, 000                 264              |
-----------------------------------------------

所以很明显，如果我们有一个大的数据集，那么像 Set 或 HashTable 这样的普通数据结构是不可行的，这里布隆过滤器就派上用场了。有关两者比较的更多详细信息，请参阅本文：Difference between Bloom filters and Hashtable

如何借助Bloom Filter来解决这些问题呢？
让我们来看一个位数组大小的N(这里是 24)并用二进制零初始化每个位，现在取一些散列函数(你可以取任意多个，我们在这里取两个哈希函数来进行说明)。

现在将您拥有的第一个 IP 传递给两个哈希函数，该函数会生成一些随机数，如下所示
```
hashFunction_1(192.170.0.1) : 2 
hashFunction_2(192.170.0.1) : 6
```
现在，转到索引 2 和 6 并将该位标记为二进制 1。
现在传递您拥有的第二个IP，并按照相同的步骤操作。
```
hashFunction_1(75.245.10.1) : 4 
hashFunction_2(75.245.10.1) : 10
```
现在，转到索引 4 和 10 并将该位标记为二进制 1。
同样将第三个 IP 传递给两个哈希函数，并假设您得到了哈希函数的以下输出
```
hashFunction_1(10.125.22.20) : 10 
hashFunction_2(10.125.22.20) : 19
```
'
现在，转到索引 10 和 19 并将其标记为二进制 1，这里索引 10 已被前一个条目标记，因此只需将索引 19 标记为二进制 1。

现在，是时候检查数据集中是否存在 IP 了，

测试输入#1
假设我们要检查 IP75.245.10.1。使用我们用于添加上述输入的相同的两个哈希函数传递此 IP。
```
hashFunction_1(75.245.10.1) : 4 
hashFunction_2(75.245.10.1) : 10
```
现在，转到索引并检查该位，如果索引 4 和 10 都标记为二进制 1，则 IP 75.245.10.1 存在于集合中，否则它不存在于数据集中。
测试输入#2
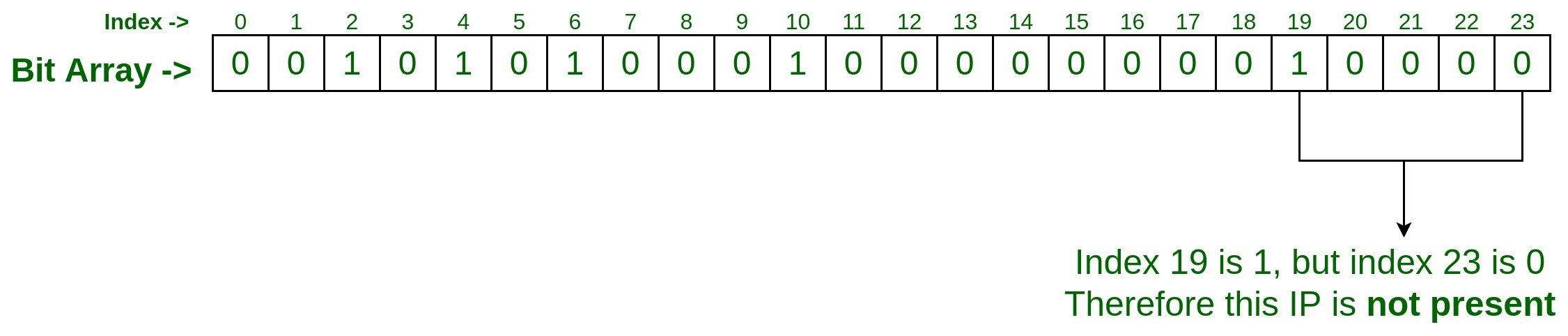
假设我们要检查 IP75.245.20.30是否存在于集合中？因此，过程将是相同的，使用我们用于添加上述输入的相同的两个哈希函数传递此 IP。
```
hashFunction_1(75.245.20.30) : 19 
hashFunction_2(75.245.20.30) : 23
```
由于在索引 19 处它被设置为 1，但在索引 23 处它被设置为 0，所以我们可以说给定的 IP 75.245.20.30 不存在于集合中。

为什么布隆过滤器是概率数据结构？
让我们通过另一个测试来理解这一点，这次考虑一个 IP101.125.20.22并检查它是否存在于集合中。将其传递给两个哈希函数。考虑我们的哈希函数结果如下。

hashFunction_1(101.125.20.22) : 19 
hashFunction_2(101.125.20.22) : 2

现在，访问索引 19 和 2(设置为 1)，它表示给定的 IP101.125.20.22 存在于集合中。

但是，这个 IP 101.125.20.22 已在上面的数据集中进行了处理，同时将 IP 添加到位数组中。这称为误报：

Expected Output: No
Actual Output: Yes (False Positive)

在本例中，索引 2 和 19 被其他输入设置为 1，而不是被该 IP 101.125.20.22 设置为 1。这就是所谓的碰撞，这就是为什么它是概率性的，发生的可能性不是 100%。

对布隆过滤器有何期望？

当布隆过滤器表示某个元素是不存在这是肯定不存在。它保证 100% 给定的元素在集合中不可用，因为哈希函数给出的索引的任何一位都将被设置为 0。
但是当布隆过滤器说给定元素是展示这是不是100%确定，因为可能由于冲突，哈希函数给出的索引的所有位都被其他输入设置为 1。

如何从布隆过滤器获得 100% 准确的结果？
那么，这只能通过采用更多数量的哈希函数来实现。我们采用的哈希函数数量越多，得到的结果就越准确，因为发生冲突的机会就越小。

布隆过滤器的时间和空间复杂度
假设我们周围有4000万个数据集我们正在使用周围H 哈希函数，然后：

Time complexity: O(H), where H is the number of hash functions used
Space complexity: 159 Mb (For 40 million data sets)
Case of False positive: 1 mistake per 10 million (for H = 23)

使用 Guava 库在 Java 中实现布隆过滤器：
我们可以使用以下方法来实现布隆过滤器Guava 提供的 Java 库.

包括以下 Maven 依赖项：


<dependency> 
    <groupId>com.google.guava</groupId> 
    <artifactId>guava</artifactId> 
    <version>19.0</version> 
</dependency>

编写以下代码来实现布隆过滤器：


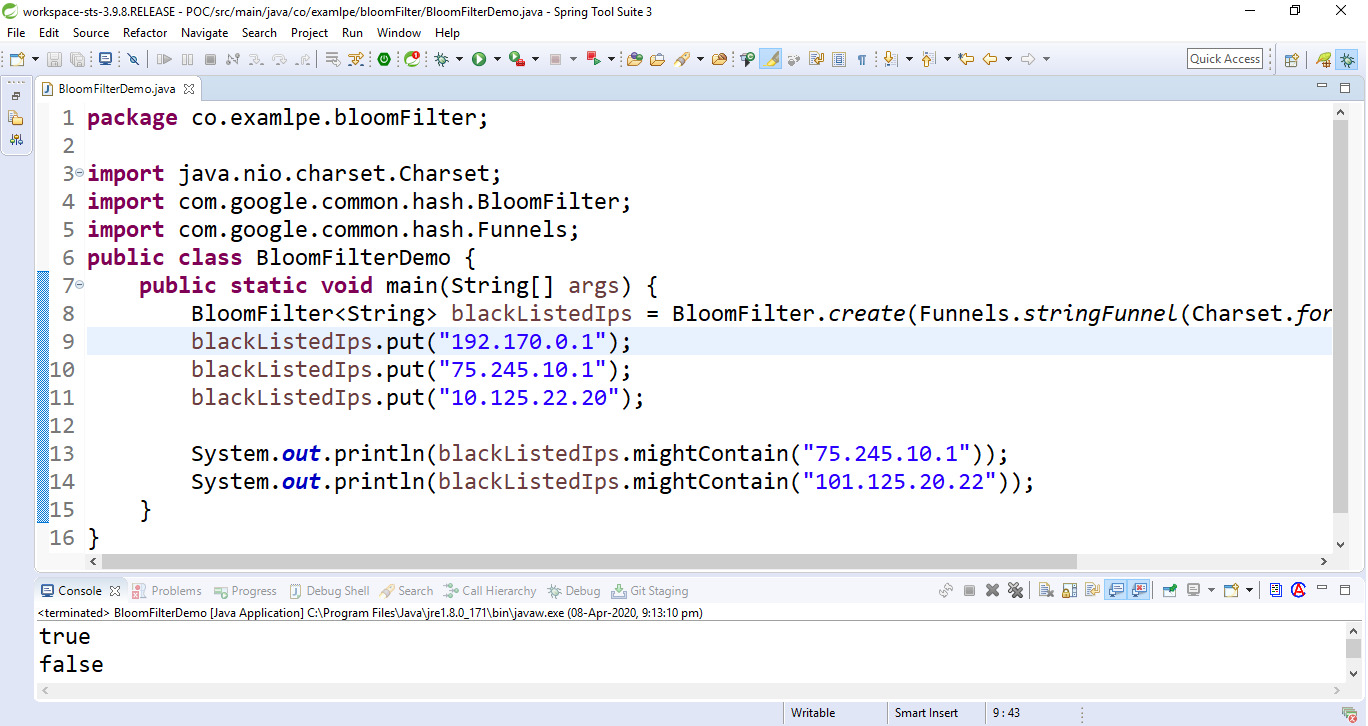
// Java program to implement 
// Bloom Filter using Guava Library 
  
import java.nio.charset.Charset; 
import com.google.common.hash.BloomFilter; 
import com.google.common.hash.Funnels; 
  
public class BloomFilterDemo { 
    public static void main(String[] args) 
    { 
  
        // Create a Bloom Filter instance 
        BloomFilter<String> blackListedIps 
            = BloomFilter.create( 
                Funnels.stringFunnel( 
                    Charset.forName("UTF-8")), 
                10000); 
  
        // Add the data sets 
        blackListedIps.put("192.170.0.1"); 
        blackListedIps.put("75.245.10.1"); 
        blackListedIps.put("10.125.22.20"); 
  
        // Test the bloom filter 
        System.out.println( 
            blackListedIps 
                .mightContain( 
                    "75.245.10.1")); 
        System.out.println( 
            blackListedIps 
                .mightContain( 
                    "101.125.20.22")); 
    } 
}

输出：

布隆过滤器输出

Note: The above Java code may return a 3% false-positive probability by default.

降低false-positive概率
在Bloom Filter对象创建中引入另一个参数，如下：
BloomFilter blackListedIps = BloomFilter.create(Funnels.stringFunnel(Charset.forName("UTF-8")), 10000, 0.005);
现在false-positive概率已从0.03减少到0.005。但调整此参数会对布隆过滤器产生影响。

降低误报概率的效果：
我们从哈希函数、数组位、时间复杂度和空间复杂度来分析这种影响。

让我们看看不同数据集的插入时间。

-----------------------------------------------------------------------------
|Number of UUIDs | Set Insertion Time(ms)  | Bloom Filter Insertion Time(ms) |
-----------------------------------------------------------------------------
|10                         <1                   71                          |   
|100                         3                   17                          |
|1, 000                      58                  84                          |
|10, 000                     122                 272                         |
|100, 000                    836                 556                         |
|1, 000, 000                 7395                5173                        |
------------------------------------------------------------------------------

现在，让我们看一下内存(JVM 堆)

--------------------------------------------------------------------------
|Number of UUIDs | Set JVM heap used(MB) | Bloom filter JVM heap used(MB) | 
--------------------------------------------------------------------------
|10                         <2                   0.01                     |   
|100                        <2                   0.01                     |
|1, 000                      3                   0.01                     |
|10, 000                     9                   0.02                     |
|100, 000                    37                  0.1                      |
|1, 000, 000                 264                 0.9                      |
---------------------------------------------------------------------------

位计数

----------------------------------------------
|Suggested size of Bloom Filter  | Bit count  |
----------------------------------------------
|10                                40         |   
|100                               378        |
|1, 000                            3654       |
|10, 000                           36231      |
|100, 000                          361992     |
|1, 000, 000                       3619846    |
-----------------------------------------------

用于各种误报概率的哈希函数数量：

-----------------------------------------------
|Suggested FPP of Bloom Filter | Hash Functions|
-----------------------------------------------
|3%                                5           |   
|1%                                7           |
|0.1%                              10          |
|0.01%                             13          |
|0.001%                            17          |
|0.0001%                           20          |
------------------------------------------------

结论：

因此可以说，当我们必须以低内存消耗处理大数据集的情况下，布隆过滤器是一个不错的选择。此外，我们想要更准确的结果，必须增加哈希函数的数量。

相关用法

注：本文由纯净天空筛选整理自asadaliasad大神的英文原创作品 Bloom Filter in Java with Examples。非经特殊声明，原始代码版权归原作者所有，本译文未经允许或授权，请勿转载或复制。