当前位置: 首页>>算法&结构>>正文

维特比算法(Viterbi Algorithm)

@ ▣算法&结构, 算法的力量 ♢, , ,

本分摘录翻译自wikipedia Viterbi algorithm。
维特比算法(Viterbi algorithm)是一种动态规划算法，它用于寻找最可能产生观测到的事件的序列，这个序列是隐含状态序列，也叫维特比路径(Viterbi path)。最典型的应用场景是马尔科夫信息源上下文和隐马尔科夫模型(HMM)。
该算法广泛应用于通信技术中的解卷积码，例如：CDMA、GSM数字蜂窝网、拨号调制解调器、卫星、深空通信以及802.11无线网。当前，该算法也经常用于语音识别、语音合成、说话人分割（diarization, 姑且这么翻译，它的意思是将同一段语音中不同人的话语归为一类）[1] 、关键词识别、计算语言学、生物信息学中。例如，在语音转文本中（语音识别），声音信号作为观察到的事件序列，而文本序列作为声音信号的隐含原因。对于给定的声音信号，维特比算法找出最可能的文本序列。

历史(History)

维特比算法是以Andrew Viterbi 的名字来命名的，他在1967年提出了这个算法，作为含噪声的数字通信链路中卷积码的解码方法。[2] 不过，该算法具有multiple invention的历史——至少有7个独立的发明者，包括：Viterbi, Needleman and Wunsch, and Wagner and Fischer.[3] “维特比（路径，算法）”已经成为使用动态规划解决概率最大化问题的标准术语。[3] 例如，在statistical parsing中，对于一个单词序列，动态规划算法能找到最可能上下文无关的语法分析结果，通常称之为“维特比分析”。[4][5][6]

算法(Algorithm)

假设在一个隐马尔科模型(HMM)中，状态空间为S, 状态i的初始概率为πi, 状态i到j的转移概率为ai,j。观察到的值为y1, y2, …, yT 。产生观察值的最可能状态序列是x1, x2, …, xT通过下面的迭代关系给出：[7] 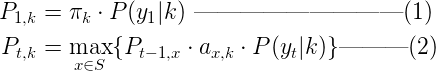gif.latex其中Pt,k是以k为最终状态的前t个观察值对应的最可能的状态序列的概率, P(yt|k)是在隐含状态k对应观察值yt的生成概率。维特比路径可以通过保存等式(2)中用到的x的反向指针得到。
根据公式（2），维特比算法计算中需要考察每个状态的|S|个值和前一状态的|S|个值从而计算当前最佳，即每个状态需要O(|S|2)次计算，总共的状态数量为T,所以总的时间复杂度为: O(T × |S|2)。

实例(Example)

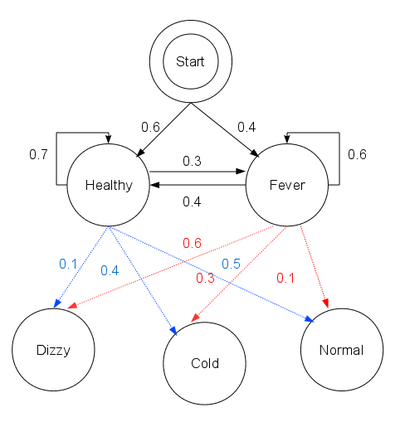
以乡村中原始的小诊所为例。村民只有两种简单的属性：健康或者发烧。他们只能通过诊所的医生知道自己是否发烧。聪明的医生通过询问病人感觉如何来诊断是否发烧；村民的回答是：正常、头晕、寒冷三者之一。
假设某病人每天都来诊所告诉医生她感觉如何。医生认为病人的健康状况是一个离散的马尔科夫链（Markov chain）。有两种状态“Healthy”和”Fever”，但是医生没法直接观察到，也就是说这两个状态对医生来说是隐藏(hidden)的。每天，病人会基于自身健康状况，以某个几率告诉医生他的感觉：可能是”normal”、”cold”或”dizzy”三者之一，这些事观察值。这里的整个系统可以看做是隐马尔科夫模型（HMM）。
医生了解村民通常的健康状况，以及是否有发热情况下的症状。也就是说，HMM的参数是已知的。这可以表示为下面的Python变成语言：

//初始状态
states = ('Healthy', 'Fever')

//观察值
observations = ('normal', 'cold', 'dizzy')
 
//初始概率
start_probability = {'Healthy': 0.6, 'Fever': 0.4}
 
//转移概率
transition_probability = {
   'Healthy' : {'Healthy': 0.7, 'Fever': 0.3},
   'Fever' : {'Healthy': 0.4, 'Fever': 0.6}
   }

//生成概率
emission_probability = {
   'Healthy' : {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
   'Fever' : {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6}
   }

这段代码中，start_probability表示病人第一次去诊所时医生认为他属于HMM某个状态的经验知识（医生所知道的只有病人更倾向于健康，0.6的概率为Healthy, 0.4的概率为Fever）。transition_probability表示马尔科夫链中的健康情况转变。在上述例子中，如果病人今天是Healthy那么明天有30%的几率是Fever. emission_probability表示的是在不同的健康状况下不同感觉的可能性，这个可以称为生成概率，也可以叫做状态发射概率。比如：如果他是Healthy的，那么感觉是normal的概率是50%；如果是Fever, 感觉dizzy的概率是60%。

400px-An_example_of_HMM

某病人连续三天就诊，医生了解到第一天她感觉是normal, 第二天是cold, 第三天是dizzy。医生的疑问是：最能解释对病人的这些观察值的健康状态序列是什么？这个问题可以通过维特比算法来回答。

def viterbi(obs, states, start_p, trans_p, emit_p):
    V = [{}]
    path = {}
 
    # Initialize base cases (t == 0)
    for y in states:
        V[0][y] = start_p[y] * emit_p[y][obs[0]]
        path[y] = [y]
 
    # Run Viterbi for t > 0
    for t in range(1, len(obs)):
        V.append({})
        newpath = {}
 
        for y in states:
            (prob, state) = max((V[t-1][y0] * trans_p[y0][y] * emit_p[y][obs[t]], y0) for y0 in states)
            V[t][y] = prob
            newpath[y] = path[state] + [y]
 
        # Don't need to remember the old paths
        path = newpath
    n = 0           # if only one element is observed max is sought in the initialization values
    if len(obs) != 1:
        n = t
    print_dptable(V)
    (prob, state) = max((V[n][y], y) for y in states)
    return (prob, path[state])
 
# Don't study this, it just prints a table of the steps.
def print_dptable(V):
    s = "    " + " ".join(("%7d" % i) for i in range(len(V))) + "\n"
    for y in V[0]:
        s += "%.5s: " % y
        s += " ".join("%.7s" % ("%f" % v[y]) for v in V)
        s += "\n"
    print(s)

viterbi函数有如下参数: obs 是观察值序列，例如[‘normal’, ‘cold’, ‘dizzy’]; states是隐含的状态；start_p是初始概率；trans_p是转移概率；emit_p是发射概率（生成概率）。为了代码的简介性，我们假设obs是非空的并且trans_p[i][j]和emit_p[i][j]对所有的状态i,j都有值。
运行上述函数的代码如下：


def example(): 
       return viterbi(observations, states, start_probability, transition_probability, emission_probability) 
print(example())

 

程序显示最可能产生观察值[‘normal’, ‘cold’, dizzy’]的状态是[‘Healthy’, ‘Healthy’, ‘Fever’].也就是说，给定观察到的活动，病人最可能在第一天和第二天都是Healthy的，她第一天感觉正常第二天感觉冷，第三天的时候就确定开始发热了。
维特比算法的操作可以通过篱笆网络图 trellis diagram来可视化。维特比路径本质上就是通过篱笆网络的最短路径。诊所的例子对应的篱笆网络如下；对应的维特比路径被加粗显示。（注，Day3第一帧右下角的概率应该是P(‘dizzy’|newstat)）

Animation of the trellis diagram for the Viterbi algorithm. After Day 3, the most likely path is ['Healthy', 'Healthy', 'Fever']

当实现维特比算法的时候，需要注意的是很多语言使用浮点运算，由于p很小，这会导致运算结果的溢出(underflow)。避免这个问题的常用技术是使用概率的对数运算（logarithm of the probabilities ）。一旦算法运行完毕，可以通过合适的指数运算来取得概率的准确值。

扩展(Extensions)

有一种维特比算法的泛化算法称为max-sum algorithm(也叫max-product algorithm), 在大量图模型（例如贝叶斯网络(Bayesian networks), 马尔科夫随机场(Markov random fields) 和 条件随机场( conditional random fields )). ）中，该算法可用于寻找全部或者部分隐含变量( latent variables )的值。
使用迭代维特比解码(iterative Viterbi decoding)算法，对于给定的HMM我们可以找到观察值子序列的最佳匹配。
另外一种算法是最近提出的Lazy Viterbi algorithm，该算法在实践中比原来的维特比算法有更好的性能，因为该算只在实际需要的时候才进行节点扩展。

伪代码(Pseudocode)

给定观察值空间O = {o1, o2, …, oN}；状态空间S = {s1, s2, …, sK}, 观察值序列Y={y1, y2, …, yT}；转移矩阵A(K×K), 其中Aij存储状态si到状态sj的转移概率；生成矩阵B(K×N), 其中Bij存储从状态si生成观察值oj的概率；大小为K的初始概率数组π, 其中πi存储x1 = Si的概率。设X = {x1, x2, …, xT}是生成观察值Y={y1, y2, …, yT}的状态序列。
在这个动态规划问题中，我们构造两个二维表T1, T2(大小均为K×T)。T1 的元存概率，T2的元素存路径。基于上述定义的伪代码如下：3

参阅(See also)

Notes

  1. Xavier Anguera et Al, “Speaker Diarization: A Review of Recent Research”, retrieved 19. August 2010, IEEE TASLP
  2. 29 Apr 2005, G. David Forney Jr: The Viterbi Algorithm: A Personal History
  3. Daniel Jurafsky; James H. Martin. Speech and Language Processing. Pearson Education International. p. 246.
  4. Schmid, Helmut (2004). Efficient parsing of highly ambiguous context-free grammars with bit vectors (PDF). Proc. 20th Int’l Conf. on Computational Linguistics (COLING). doi:10.3115/1220355.1220379. edit
  5. Klein, Dan; Manning, Christopher D. (2003). A* parsing: fast exact Viterbi parse selection (PDF). Proc. 2003 Conf. of the North American Chapter of the Association for Computational Linguistics on Human Language Technology (NAACL). pp. 40–47. doi:10.3115/1073445.1073461. edit
  6. Stanke, M.; Keller, O.; Gunduz, I.; Hayes, A.; Waack, S.; Morgenstern, B. (2006). “AUGUSTUS: Ab initio prediction of alternative transcripts”. Nucleic Acids Research 34: W435. doi:10.1093/nar/gkl200. edit
  7. Xing E, slide 11
  8. Qi Wang; Lei Wei; Rodney A. Kennedy (2002). “Iterative Viterbi Decoding, Trellis Shaping,and Multilevel Structure for High-Rate Parity-Concatenated TCM”. IEEE Transactions on Communications 50: 48–55. doi:10.1109/26.975743.
  1. A fast maximum-likelihood decoder for convolutional codes (PDF). Vehicular Technology Conference. December 2002. pp. 371–375. doi:10.1109/VETECF.2002.1040367.

References

实现（Implementations）

外部链接(External links)

本文由《纯净天空》出品。文章地址: https://vimsky.com/article/863.html，未经允许，请勿转载。