下面是章节频繁模式挖掘的内容(其他内容参见全文目录)
频繁项集挖掘是通常是大规模数据分析的第一步,多年以来它都是数据挖掘领域的活跃研究主题。建议用户参考维基百科的association rule learning 了解更多信息。MLlib支持了一个并行的FP-growth,FP-growth是很受欢迎的频繁项集挖掘算法。
FP-growth
FP-growth算法在论文Han et al., Mining frequent patterns without candidate generation 中有详细论述,其中FP指的是频繁模式(frequent pattern)。给定一个事务数据集,FP-growth算法的第一步是计算项的频度并标记频繁项。跟Apriori这类挖掘频繁项集算法不同的是,FP-growth的第二步使用了一个FP-tree结构来编码事务。第二部之后,频繁项集可以直接从FP-tree中提取。在MLlib中,我们实现了一个FP-growth的并行版本(PFP),具体方法参见论文Li et al., PFP: Parallel FP-growth for query recommendation。
MLlib中FP-growth实现的参数:
minSupport: 最小支持度。用浮点数表示比例。例如某项在5个事务中出现3次,其支持度为3/5=0.6。numPartitions: 计算的分区数量。
示例(scala)
FPGrowth 实现了 FP-growth 算法. 其输入是事务RDD, 每个事务是一个可遍历的项集。 调用 FPGrowth.run 返回FPGrowthModel ,它存储的是频繁项集以及对应频度。
import org.apache.spark.rdd.RDD
import org.apache.spark.mllib.fpm.{FPGrowth, FPGrowthModel}
val transactions: RDD[Array[String]] = ...
val fpg = new FPGrowth()
.setMinSupport(0.2)
.setNumPartitions(10)
val model = fpg.run(transactions)
model.freqItemsets.collect().foreach { itemset =>
println(itemset.items.mkString("[", ",", "]") + ", " + itemset.freq)
}
补充:
1. Apriori求频繁项集的基本原理(有点像数学归纳法):
- 首先找到频繁1项集(大于支持度的单项)
- 由k项集生成k+1项集,生成的方式是:将k项集中的元素两两组合(求并集),大于支持度的作为k+1项集。
2. FP-Growth算法求频繁项集的基本原理:
- 首先对单项按频度排序,去掉小于支持度的项
- 对每一条记录,对项按1中计算的频度排序。
- 将记录依次插入到FP-Tree(一个前缀共享树)
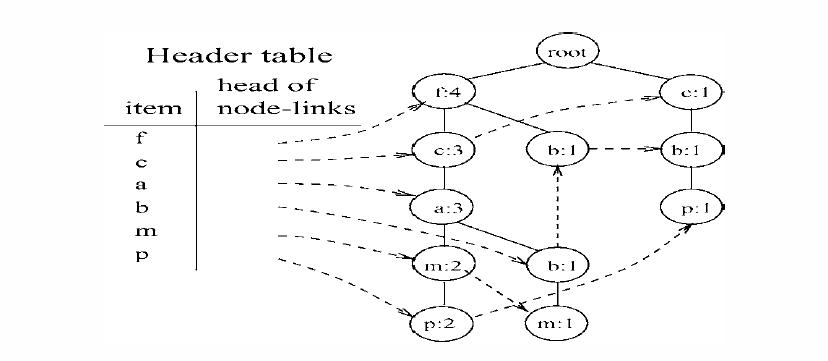
- 为相同的节点增加头表结构(见下图)。
- 找到每个头表项的条件模式基(CPB),保留后缀,将CPB作为新的数据集,回到开始递归处理(树节点为空是,输出头表项+后缀)
参考:
[1] http://zh.wikipedia.org/wiki/%E5%85%B3%E8%81%94%E5%BC%8F%E8%A7%84%E5%88%99
[2] http://www.cnblogs.com/zhangchaoyang/articles/2198946.html
[3] http://hi.baidu.com/nefzpohtpndhovr/item/9d5c371ba2dbdc0ed1d66dca