pr_curve() 構造全精度召回曲線並返回一個 tibble。請參閱 pr_auc() 了解精度召回曲線下的麵積。
用法
pr_curve(data, ...)
# S3 method for data.frame
pr_curve(
data,
truth,
...,
na_rm = TRUE,
event_level = yardstick_event_level(),
case_weights = NULL
)參數
- data
-
包含
truth和...指定的列的data.frame。 - ...
-
一組不帶引號的列名稱或一個或多個
dplyr選擇器函數,用於選擇哪些變量包含類概率。如果truth是二進製,則僅應選擇 1 列,並且它應對應於event_level的值。否則,列的數量應與truth的因子級別一樣多,並且列的順序應與truth的因子級別相同。 - truth
-
真實類結果的列標識符(即
factor)。這應該是一個不帶引號的列名,盡管此參數是通過表達式傳遞的並且支持quasiquotation(您可以不帶引號的列名)。對於_vec()函數,一個factor向量。 - na_rm
-
logical值,指示在計算繼續之前是否應剝離NA值。 - event_level
-
單個字符串。
"first"或"second"指定將truth的哪個級別視為"event"。此參數僅適用於estimator = "binary"。默認使用內部幫助程序,通常默認為"first",但是,如果設置了已棄用的全局選項yardstick.event_first,則將使用該幫助程序並發出警告。 - case_weights
-
案例權重的可選列標識符。這應該是一個不帶引號的列名稱,其計算結果為
data中的數字列。對於_vec()函數,一個數值向量。
細節
pr_curve() 計算概率列的每個唯一值(除了無窮大)的精度。
有一個ggplot2::autoplot() 方法可以快速可視化曲線。這適用於二進製和多類輸出,也適用於分組數據(即來自重新采樣)。請參閱示例。
多級
如果提供了多類 truth 列,則將采用 one-vs-all 方法來計算多條曲線,每個級別一條。在這種情況下,將有一個附加列 .level ,用於標識 one-vs-all 計算中的 "one" 列。
相關級別
在計算二元分類指標時,對於哪個因子級別應自動被視為 "event" 或 "positive" 結果,沒有通用約定。在 yardstick 中,默認使用第一級。要更改此設置,請將參數 event_level 更改為 "second" 以將因子的最後一個級別視為感興趣級別。對於涉及 one-vs-all 比較(例如宏平均)的多類擴展,此選項將被忽略,並且 "one" 級別始終是相關結果。
也可以看看
使用 pr_auc() 計算精確召回曲線下的麵積。
其他曲線指標:gain_curve()、lift_curve()、roc_curve()
例子
# ---------------------------------------------------------------------------
# Two class example
# `truth` is a 2 level factor. The first level is `"Class1"`, which is the
# "event of interest" by default in yardstick. See the Relevant Level
# section above.
data(two_class_example)
# Binary metrics using class probabilities take a factor `truth` column,
# and a single class probability column containing the probabilities of
# the event of interest. Here, since `"Class1"` is the first level of
# `"truth"`, it is the event of interest and we pass in probabilities for it.
pr_curve(two_class_example, truth, Class1)
#> # A tibble: 501 × 3
#> .threshold recall precision
#> <dbl> <dbl> <dbl>
#> 1 Inf 0 1
#> 2 1.00 0.00388 1
#> 3 1.00 0.00775 1
#> 4 1.00 0.0116 1
#> 5 1.00 0.0155 1
#> 6 1.00 0.0194 1
#> 7 1.00 0.0233 1
#> 8 1.00 0.0271 1
#> 9 1.00 0.0310 1
#> 10 1.00 0.0349 1
#> # ℹ 491 more rows
# ---------------------------------------------------------------------------
# `autoplot()`
# Visualize the curve using ggplot2 manually
library(ggplot2)
library(dplyr)
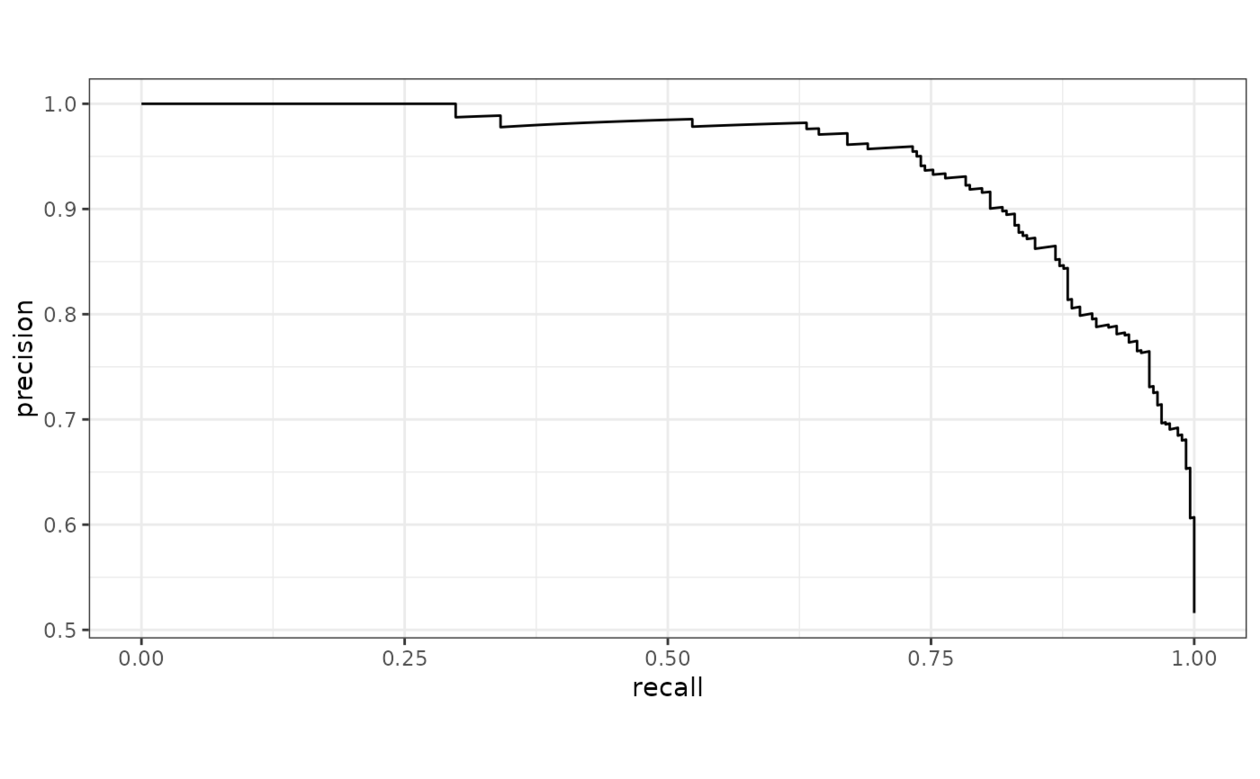
pr_curve(two_class_example, truth, Class1) %>%
ggplot(aes(x = recall, y = precision)) +
geom_path() +
coord_equal() +
theme_bw()
 # Or use autoplot
autoplot(pr_curve(two_class_example, truth, Class1))
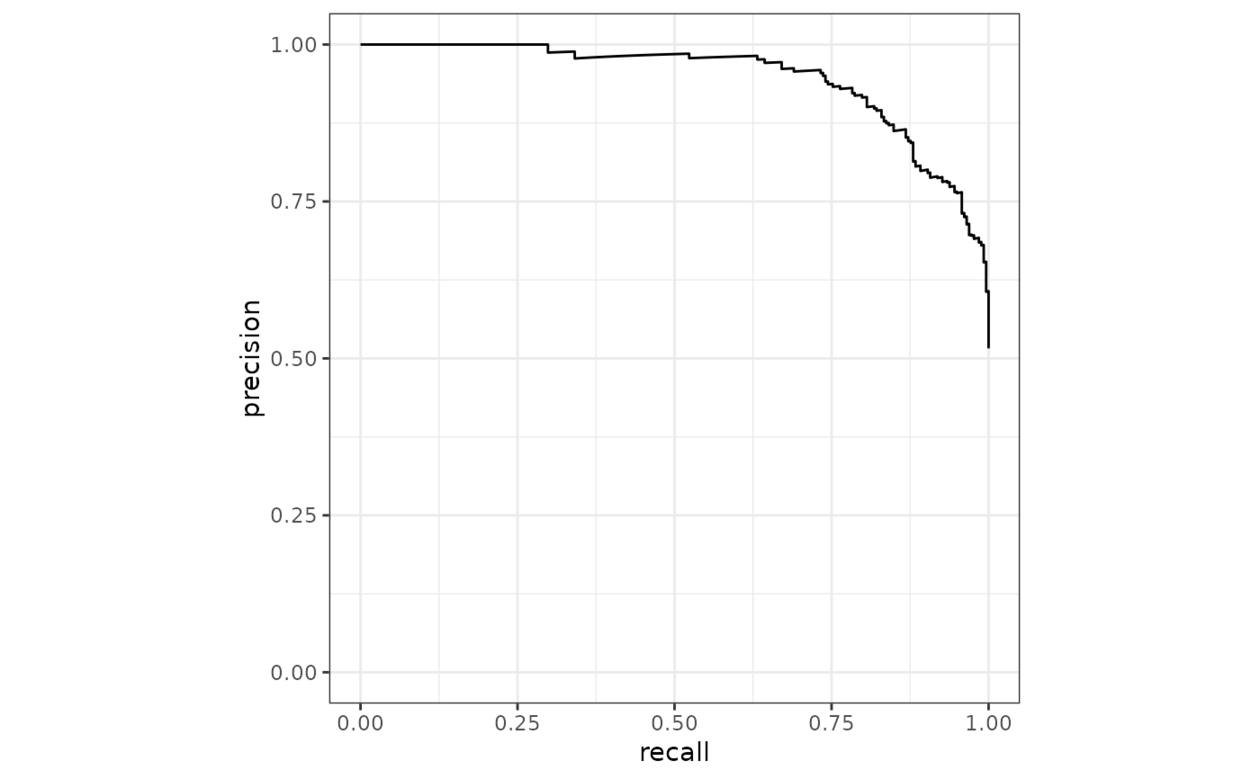
# Or use autoplot
autoplot(pr_curve(two_class_example, truth, Class1))
 # Multiclass one-vs-all approach
# One curve per level
hpc_cv %>%
filter(Resample == "Fold01") %>%
pr_curve(obs, VF:L) %>%
autoplot()
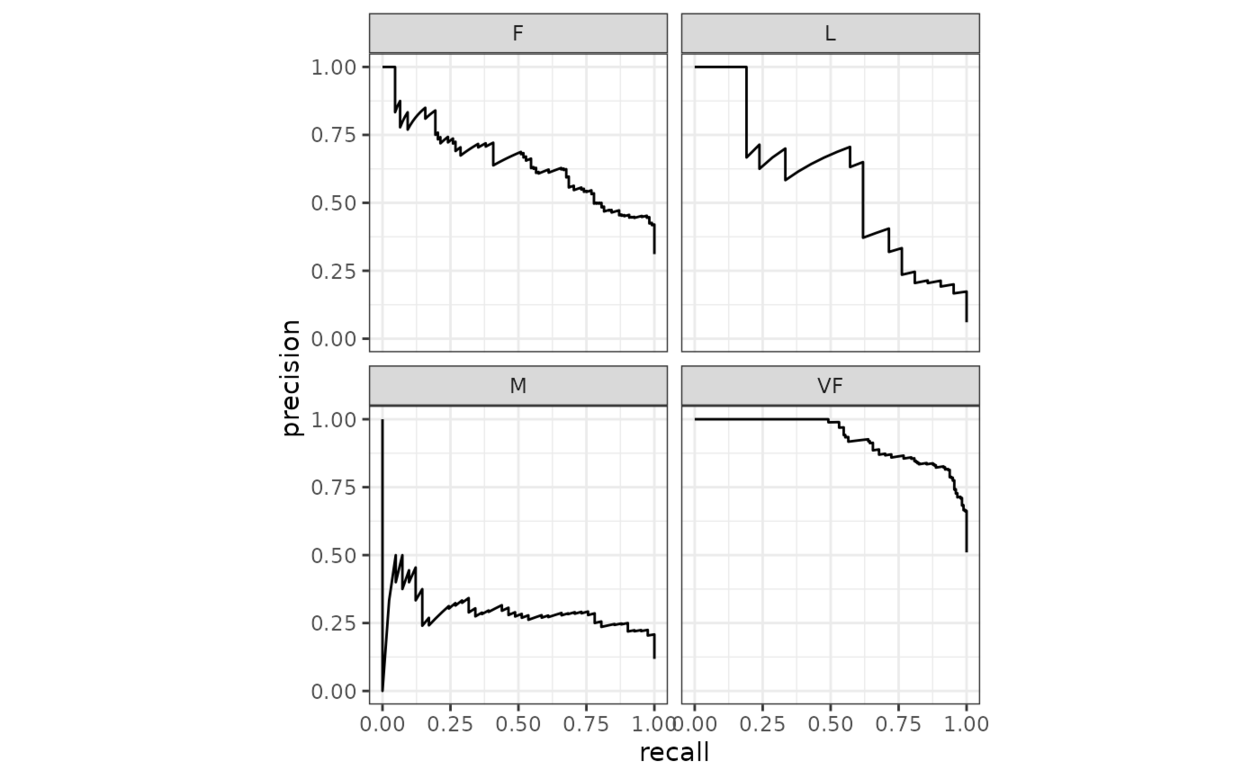
# Multiclass one-vs-all approach
# One curve per level
hpc_cv %>%
filter(Resample == "Fold01") %>%
pr_curve(obs, VF:L) %>%
autoplot()
 # Same as above, but will all of the resamples
hpc_cv %>%
group_by(Resample) %>%
pr_curve(obs, VF:L) %>%
autoplot()
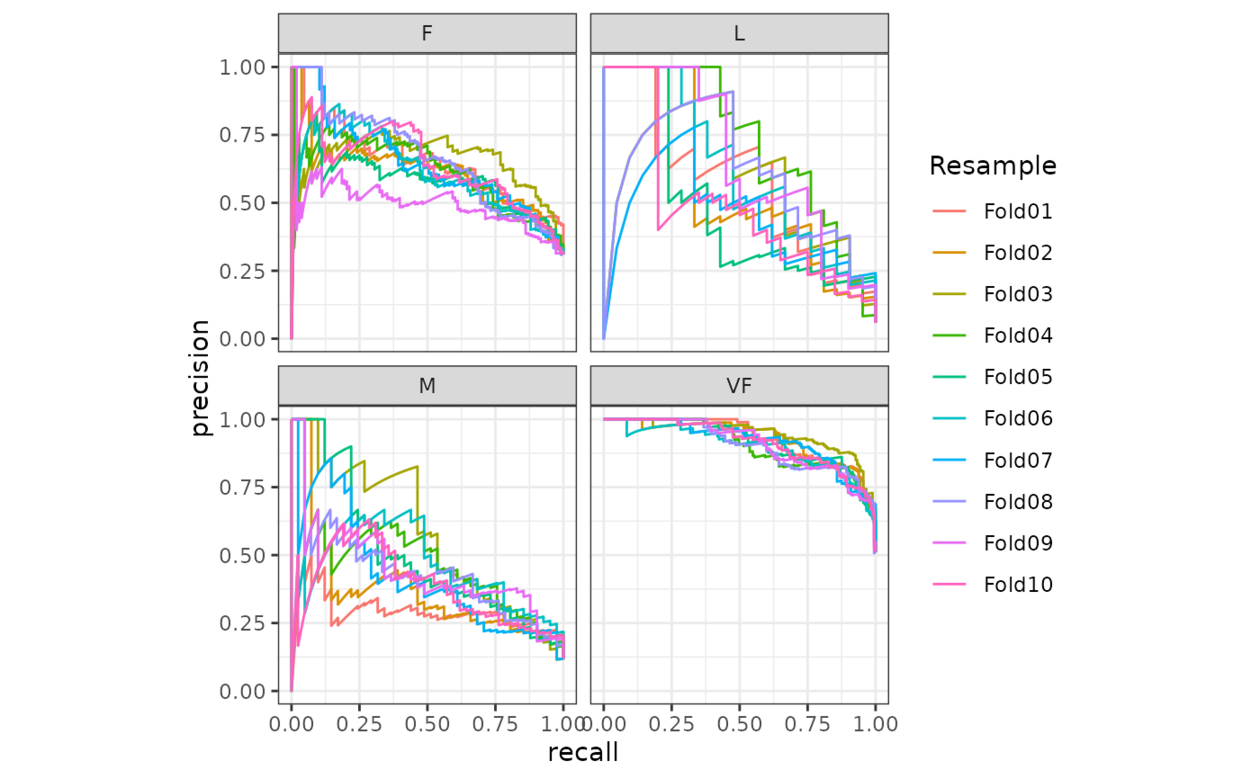
# Same as above, but will all of the resamples
hpc_cv %>%
group_by(Resample) %>%
pr_curve(obs, VF:L) %>%
autoplot()
相關用法
- R yardstick pr_auc 查準率曲線下麵積
- R yardstick precision 精確
- R yardstick poisson_log_loss 泊鬆數據的平均對數損失
- R yardstick ppv 陽性預測值
- R yardstick accuracy 準確性
- R yardstick gain_capture 增益捕獲
- R yardstick conf_mat 分類數據的混淆矩陣
- R yardstick mn_log_loss 多項數據的平均對數損失
- R yardstick rpd 性能與偏差之比
- R yardstick mae 平均絕對誤差
- R yardstick detection_prevalence 檢測率
- R yardstick bal_accuracy 平衡的精度
- R yardstick rpiq 績效與四分位間的比率
- R yardstick roc_aunp 使用先驗類別分布,每個類別相對於其他類別的 ROC 曲線下麵積
- R yardstick roc_curve 接收者算子曲線
- R yardstick rsq R 平方
- R yardstick msd 平均符號偏差
- R yardstick mpe 平均百分比誤差
- R yardstick iic 相關性理想指數
- R yardstick recall 記起
- R yardstick roc_aunu 使用均勻類別分布,每個類別相對於其他類別的 ROC 曲線下麵積
- R yardstick npv 陰性預測值
- R yardstick rmse 均方根誤差
- R yardstick sens 靈敏度
- R yardstick rsq_trad R 平方 - 傳統
注:本文由純淨天空篩選整理自Max Kuhn等大神的英文原創作品 Precision recall curve。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
