當前位置: 首頁>>技術教程>>正文

MATLAB線性回歸指南

@ ▣技術教程 ♢,

 

問題陳述

目標是通過使用線性回歸技術進行統計推斷預測，使用來自論文“(1977) Narula and Wellington, Prediction, Linear Regression and the Minimum Sum of Relative Errors, Technometrics””的數據。這個數據集為每個待預測變量(有11個不同的待預測變量)和響應變量給出了28個數據。數據見表1：

表格1：示例數據

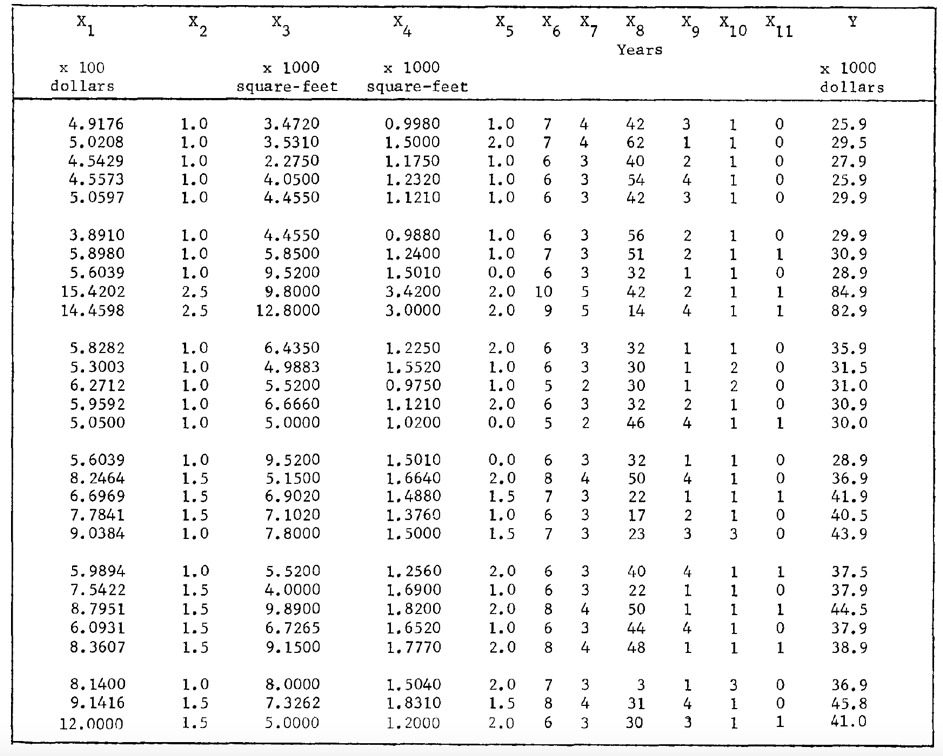
為簡單起見分析中將不包括預測變量x2，x9，x10和x11。在此數據中，變量對應於：

x1= Taxes （稅收）                x6= # of rooms （房間數）

x3= Lot size  （房屋麵積）            x7= # of bedrooms (臥室數量)

x4= Living space （居住麵積）   x8= Age of the home (房齡)

x5= # of garages  （車庫數）    y = Sale price of the home (房價)

數據結構

首先，要分析數據並查看自變量彼此之間的相關性以及與因變量的相關性，可以使用g-plot矩陣。

COMMENT ON MATLAB
data = table(observations(:, 1), observations(:, 2), observations(:, 3),...
observations(:, 4),observations(:, 5),observations(:, 6),...
observations(:, 7),observations(:, 8),'VariableNames', ...
{'x1', 'x3', 'x4', 'x5', 'x6', 'x7','x8','y'});
gplotmatrix([data.x1 data.x3 data.x4 data.x5 data.x6 data.x7 data.x8 data.y]);

圖1：預測變量和響應變量的G-plot矩陣

待預測變量和響應變量的分布及其關係可以在圖1中看到。圖中的每個單獨的軸都包括以y軸標記的變量與以x軸標記的變量的散點圖。對角線子圖顯示各個變量的直方圖，而反對角線子圖顯示其相對關係。即左上子組顯示x1預測變量的直方圖，而左上方的第二個顯示x1預測變量對x3的散點圖。從圖來看，所有預測變量均是偏斜的且與正常情況相差甚遠。在預測變量x1，x3，x4，x6和響應變量的概率分布中遇到right tail（請自行搜索分布的“右尾”）。預測變量x5采用確定的離散變量。可以說，這些預測變量和響應變量顯示的是chi-square（卡方）分布行為，而不是高斯分布行為。另一方麵，預測變量x8具有左偏分布。上述這些解釋可以通過查看其正常概率圖行為得到支持(圖2)。


COMMENT ON MATLAB
subplot(2,4,1);probplot('normal',data.x1);text(15,0.05,'x_1')
subplot(2,4,2);probplot('normal',data.x3);text(15,0.05,'x_3')
subplot(2,4,3);probplot('normal',data.x4);text(3,0.05,'x_4')
subplot(2,4,4);probplot('normal',data.x5);text(1.5,0.05,'x_5')
subplot(2,4,5);probplot('normal',data.x6);text(8,0.05,'x_6')
subplot(2,4,6);probplot('normal',data.x7);text(5,0.05,'x_7')
subplot(2,4,7);probplot('normal',data.x8);text(80,0.05,'x_8')
subplot(2,4,8);probplot('normal',data.y);text(80,0.05,'Y')

圖2：預測變量和響應變量的正態概率圖

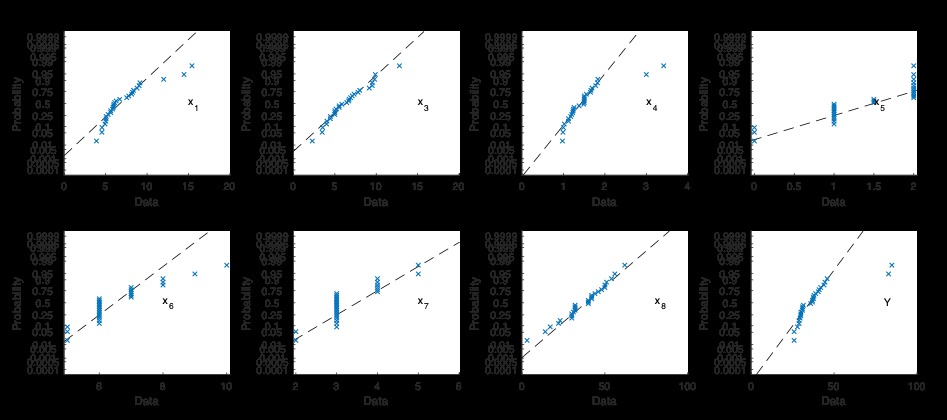
關於它們之間的關係，g-plot矩陣顯示變量的二維圖，因此從這些圖中無法理解交互作用。這就是為什麽推斷可能具有欺騙性的原因。但是，乍一看，預測變量之間的關係可以解釋如下：

表2：預測變量之間的關係

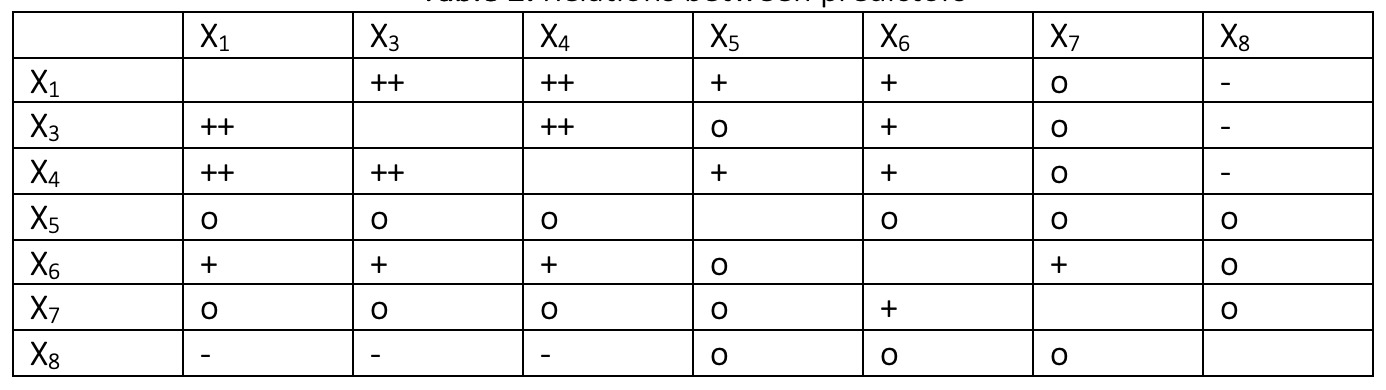
“ Double +”表示預測變量之間可能存在很強的相關性，而“ +”表示可能存在弱相關性，因為數據是如此分散。例如，x1和x3，x1和x4，x3和x4之間可能存在很強的正相關性；而x1和x5，x1和x6，x3和x6，x4和x5，x4和x6之間可能存在弱正相關性。 “—”表示x8與x1，x3，x4之間可能存在弱的負相關性。 “ o”的符號表示相關的2D圖是如此分散，很有可能是預測變量不相關。

如果我們看一下響應變量“ Y”與預測變量之間的關係，

  • 響應變量與x1，x3和x4的預測變量之間存在很強的正相關性。
  • 響應變量與x5，x6和x7的預測變量之間可能存在弱的正相關性。
  • 響應變量和x8的預測變量之間可能存在弱的負相關性。

特別是，預測變量“x1”，“x3”和“x4”與響應變量密切相關。這是有道理的，因為它們分別表示“taxes”，“lot size”和“living space”。由於車庫的數量(x5)，房間的數量(x6)和臥室的數量(x7)也影響房屋的銷售價格，因此這些預測變量與響應變量之間存在弱的正相關性。但是，主要影響似乎來自稅收，土地麵積和居住空間，這些因素比房屋的結構特性更為重要。房屋的年齡(x8)與售價之間的負相關性關係也合乎邏輯：相比舊房屋，人們更喜歡新房屋。

經驗離群值檢測

在單個預測變量空間以及由幾個預測變量定義的多元空間中是否有任何離群點？可以如下分析：

圖3：單預測空間中的觀測
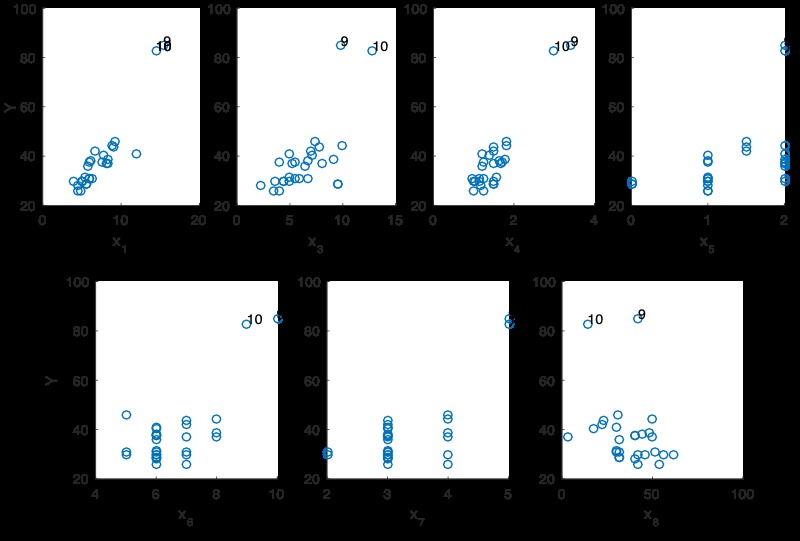
COMMENT ON MATLAB
subplot(2,4,1);scatter(data.x1, data.y);xlabel('x_1');ylabel('Y')
subplot(2,4,2);scatter(data.x3, data.y);xlabel('x_3');ylabel('Y')
subplot(2,4,3);scatter(data.x4, data.y);xlabel('x_4');ylabel('Y')
subplot(2,4,4);scatter(data.x5, data.y);xlabel('x_5');ylabel('Y')
subplot(2,4,5);scatter(data.x6, data.y);xlabel('x_6');ylabel('Y')
subplot(2,4,6);scatter(data.x7, data.y);xlabel('x_7');ylabel('Y')
subplot(2,4,7);scatter(data.x8, data.y);xlabel('x_8');ylabel('Y')

我們可以使用3D散點圖更好地查看這些關係。

COMMENT ON MATLAB
subplot(2,2,1)
scatter3(data.x1, data.x3, data.y, 50, 'ok', 'filled'), grid on
xlabel('x_1'), ylabel('x_3'), zlabel('Y');
subplot(2,2,2)
scatter3(data.x1, data.x4, data.y, 50, 'ok', 'filled'), grid on
xlabel('x_1'), ylabel('x_4'), zlabel('Y');
subplot(2,2,3)
scatter3(data.x3, data.x4, data.y, 50, 'ok', 'filled'), grid on
xlabel('x_3'), ylabel('x_4'), zlabel('Y');
subplot(2,2,4)
scatter3(data.x3, data.x8, data.y, 50, 'ok', 'filled'), grid on
xlabel('x_3'), ylabel('x_8'), zlabel('Y');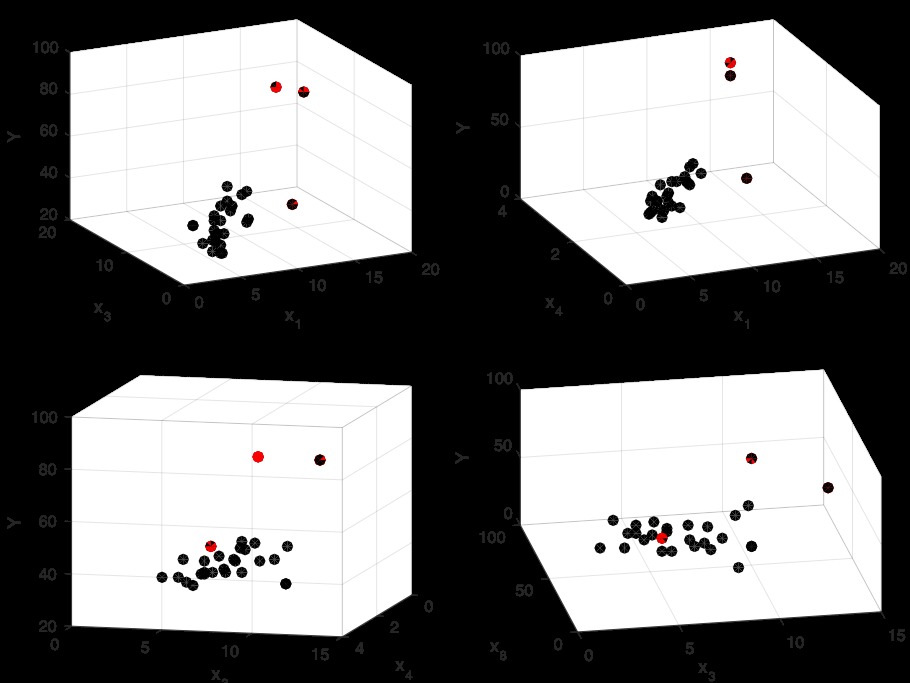

圖4：二維預測空間中的觀測

稅收和房屋麵積與響應變量之間呈正相關性。除此之外，看起來第9個點和第28個點是離群值，從二維散點圖來看，也許第10點也可能被認為太離譜。

線性回歸

在多元線性回歸中，矩陣代數是常用的方法之一。對於模型；

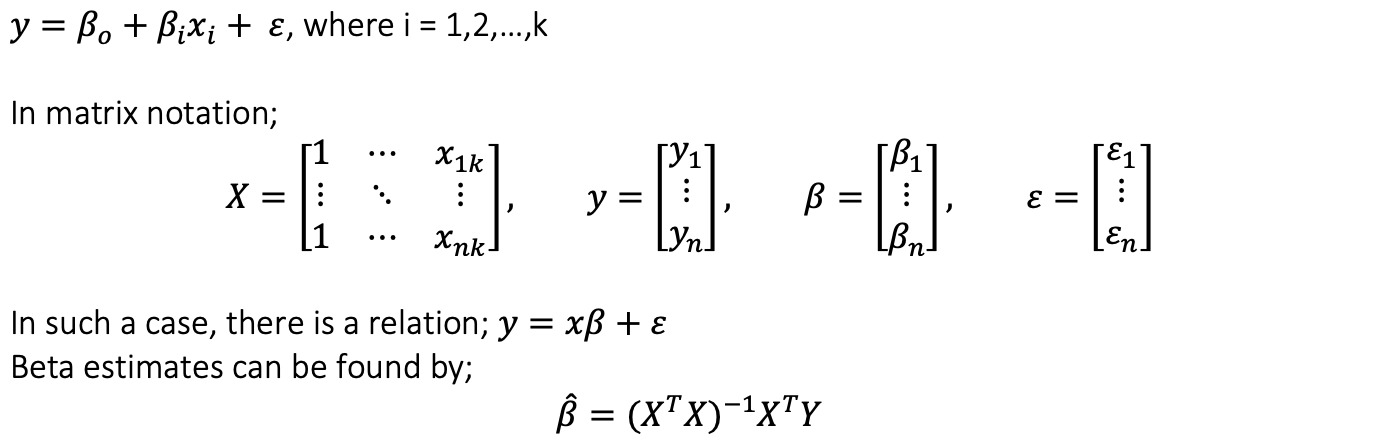
線性回歸的第一步

先構建了一個包含所有變量的線性回歸模型。

COMMENT ON MATLAB
format bank
mdl1 = fitlm(data, 'y ~ x1 + x3 + x4 + x5 + x6 + x7 + x8')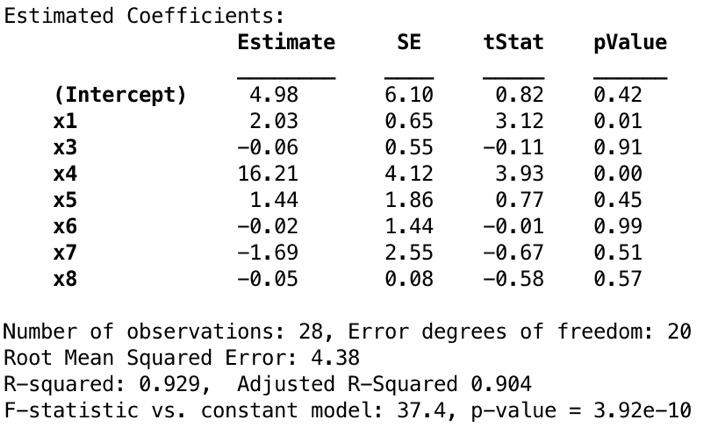

圖5：1stModel的線性回歸結果

包括所有變量可以解釋響應變量的方差，即R2和調整後的R2值相當高。從數據集中給出的所有預測變量中擬合線性模型(預測變量x2、x9、x10和x11除外）。根據上麵先前定義的關係，可以預期估計的符號。作為線性模型的結果，如果假設擬合模型為真，則預測變量x1、x4、x5與響應變量Y之間將存在正相關性，而預測變量x3、x6、x7和x8之間將存在負相關性。回想一下g-plot矩陣的最後一行，該矩陣定義了預測變量與響應變量之間的關係。

盡管預計它與預測變量x3呈強正相關性關係，但估計符號顯示出相對較弱的負相關關係。另外，響應變量與預測變量x6和x7之間的負相關性也令人驚訝。可以通過同時查看x3和x1、x4之間的強相關性來解釋第一個意外結果。此外，如果消除了杠杆點，則預測變量x6可能與響應變量顯示負相關性。 x6和x7之間的相關性可能導致正相關觀測值的多重共線性。

預測變量的p值越小，說明響應變量的行為就越重要。如果我們看線性模型擬合結果，x4(居住麵積)似乎更重要，那麽它後麵就是x1(稅)。但是，其他預測變量的p值在0.40–1的範圍內也很有意義，該值很高以至於無法確定重要的關係。這並不意味著其他預測變量(x1和x4除外)都不會對房屋的銷售價格產生影響。首先，盡管每個預測變量具有不同的單位和尺度，但我們並未對數據集進行標準化。同樣，單個p值在最後一刻添加模型時顯示了預測變量的重要性，並且預測變量之間的相關性很容易影響p值。可以應用部分測試來更清楚地了解預測變量的重要性。因此，確定預測變量是否重要還為時過早！

每個預測變量的係數受其他變量的存在影響，即我們計算的p-values都是有條件的。當模型中已經存在其餘變量時，預測變量的p-value表示通過添加該預測變量可以解釋多少響應變量。因此，預測變量對響應變量的真實效應很容易被其他變量的效應以及預測變量之間的相關性所掩蓋。我們可以通過查看方差膨脹因子(VIF)來檢查多重共線性。 VIF表示由於共線性，估計係數增加了多少。相關矩陣逆矩陣的對角線為我們提供了每個預測變量的VIF。

COMMENT ON MATLAB
diag(inv(corr(x)))

對於x1，x3，x4，x5，x6，x7和x8，結果分別為7.18、2.50、12.71、2.13、4.00、4.73、1.84和14.08。根據經驗，VIF>10意味著具有多重共線性； x3和x8似乎與其他預測變量高度相關。我們可以得出結論，多重共線性是係數估計的結果符號令人驚訝的原因之一。

通過僅在1stmodel中添加重要變量x1和x4來創建模型。

COMMENT ON MATLAB
mdl2 = fitlm(data, 'y ~ x1 + x4')

圖6：2ndModel的線性回歸結果

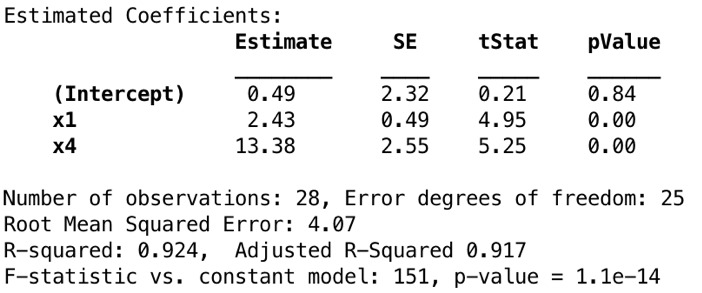
調整後的R2(0.904-> 0.917)和F-statistic(37.4-> 151)有所增加，而R2值幾乎保持恒定。我們可以得出結論，稅收x1和居住麵積x4已經可以解釋響應變量中的很多方差，而其他預測變量(例如x3和x8)似乎是不必要的。但是，我們永遠無法真正確定p-values高的預測變量，最好不要做出任何判斷。大於0.05的p-value不一定意味著應該從模型中刪除該係數，因為可能會掩蓋真實的效果。

為了了解其他預測變量的意義，我們可以應用F-test。現在的問題是：預測變量x3(房屋麵積)，x5(車庫數)，x6(房間數)，x7(臥室數)和x8(房屋年齡)是否對房價變化做出了貢獻(多個變量一起，而不是一一考慮) ！)

F統計進行部分測試；

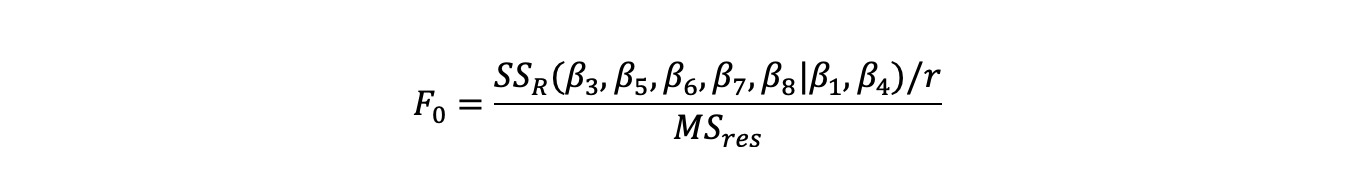
對1stand 2ndmodel進行比較，MATLAB代碼如下：

COMMENT ON MATLAB
SSR1 = mdl1.SSR
SSR2 = mdl2.SSR
MSres1 = sum(mdl1.Residuals.Raw.^2)/(mdl.NumObservations-8)
Fpartial = (SSR1-SSR2)/5/MSres1

COMMENT ON MATLAB
mdl3 = fitlm(data, 'y ~ x1 + x4 + x1^2 + x4^2 + x1:x4')

圖8：4thModel的線性回歸結果

盡管二次預測變量看起來很重要，但它們掩蓋了預測變量本身的重要性。為了簡單起見，僅將這兩個變量的相互作用添加到以下模型中。

COMMENT ON MATLAB
mdl5 = fitlm(data, 'y ~ x1 + x4 + x1:x4')

圖8：5thModel的線性回歸結果

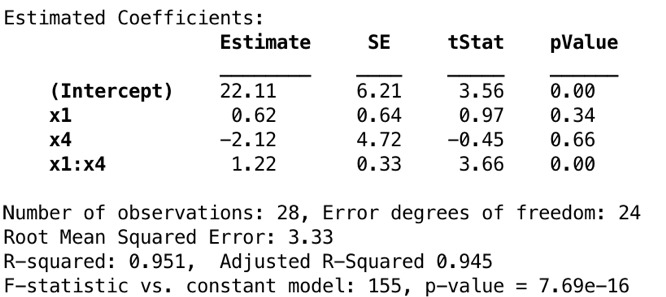
從圖8可以看出，盡管模型診斷越來越好，但是包括x1和x4的交互項掩蓋了x1和x4的顯著影響。因此，現在我們考慮僅包含x1和x4預測變量的第二個模型。

控製杠杆點和影響點

首先，有人提到第9、10和28點可能是異常值。首先，他們的杠杆作用是；

COMMENT ON MATLAB
plotDiagnostics(mdl2,'leverage','MarkerSize',8,'Marker,'o','MarkerFaceColor','k')

圖9：杠杆作用

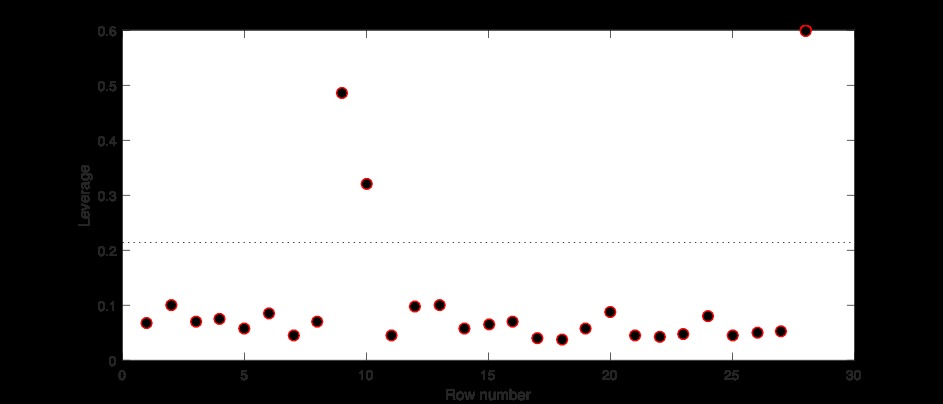
之前，當我們在預測變量的子空間x1，x2和x3中尋找杠杆點時，我們將第9、10和28個點確定為離群點。這些點的杠杆值是所有28個樣本中最高的。無論他們是否有影響力，都將分析他們的庫克距離( Cook’s distances )。

COMMENT ON MATLAB
plotDiagnostics(mdl2,'CookD','MarkerSize',8,'Marker,'o','MarkerFaceColor','r')

圖10：影響點

由於第10點和第28點可以同時視為杠杆和影響點，因此將它們從數據集中排除，然後重新考慮回歸。

重新考慮線性回歸

有影響的觀察值是那些對回歸模型的預測產生較大影響的觀察結果。杠杆點是在獨立變量的極值或偏值處進行的那些觀察值(如果有的話)，以致缺少相鄰觀察值意味著擬合的回歸模型將通過該特定觀察值。由於第10點和第28點是有影響力的點，因此將從數據集中丟棄它們，並再次考慮回歸。

COMMENT ON MATLAB
obs = observations;
obs([10 28],:) = [];
data = table(obs(:, 1), obs(:, 2), obs (:, 3),obs (:, 4),obs (:, 5),...
obs (:, 6),obs (:, 7),obs (:, 8),'VariableNames',{'x1', 'x3', 'x4', 'x5',...'x6', 'x7','x8','y'});
corr ([data.x1 data.x3 data.x4 data.x5 data.x6 data.x7 data.x8 data.y]);

相關矩陣如下：

表3：預測變量與響應變量的相關矩陣

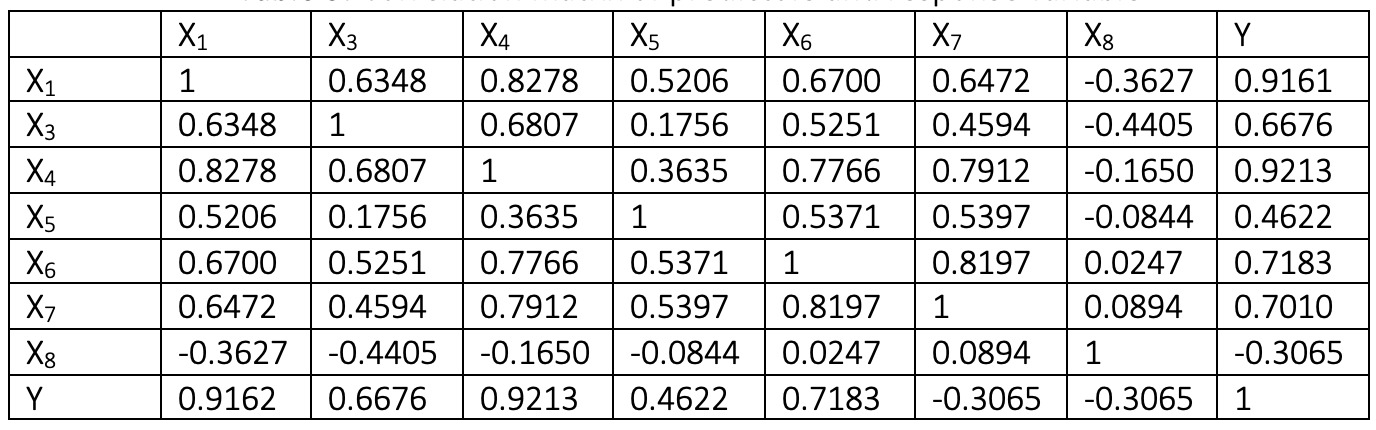
相關矩陣為我們提供了預測變量之間的相關性以及具有響應變量的預測變量的個體相關性。對於線性回歸，不希望包括線性相關的預測變量。為此，一些降維技術用於變換預測變量。可以看出，預測變量彼​​此高度相關，並且它們與響應變量(尤其是x1和x4)顯著相關。首先，將所有預測變量添加到回歸模型中。

COMMENT ON MATLAB
format bank
mdl6 = fitlm(data, 'y ~ x1 + x3 + x4 + x5 + x6 + x7 + x8')

圖11：6thModel的線性回歸結果

盡管該模型具有較高的R2值，但當涉及其p-values時，有許多無關緊要的預測變量。可能有兩個原因：預測變量之間可能存在多重共線性，和/或某些預測變量可能需要轉換。我們確信多重共線性，但對變換一無所知。為了進行檢查，為每個預測變量繪製殘差。

COMMENT ON MATLAB
subplot(2,4,1);stem(data.x1, mdl6.Residuals.Raw);xlabel('x_1');
subplot(2,4,2);stem(data.x3, mdl6.Residuals.Raw);xlabel('x_3');
subplot(2,4,3);stem(data.x4, mdl6.Residuals.Raw);xlabel('x_4');
subplot(2,4,4);stem(data.x5, mdl6.Residuals.Raw);xlabel('x_5');
subplot(2,4,5);stem(data.x6, mdl6.Residuals.Raw);xlabel('x_6');
subplot(2,4,6);stem(data.x7, mdl6.Residuals.Raw);xlabel('x_7');
subplot(2,4,7);stem(data.x8, mdl6.Residuals.Raw);xlabel('x_8');
subplot(2,4,1);plotAdjustedResponse(mdl6,'x1')
subplot(2,4,2);plotAdjustedResponse(mdl6,'x3')
subplot(2,4,3);plotAdjustedResponse(mdl6,'x4')
subplot(2,4,4);plotAdjustedResponse(mdl6,'x5')
subplot(2,4,5);plotAdjustedResponse(mdl6,'x6')
subplot(2,4,6);plotAdjustedResponse(mdl6,'x7')
subplot(2,4,7);plotAdjustedResponse(mdl6,'x8')

圖12：殘差圖

圖13：調整後的響應圖

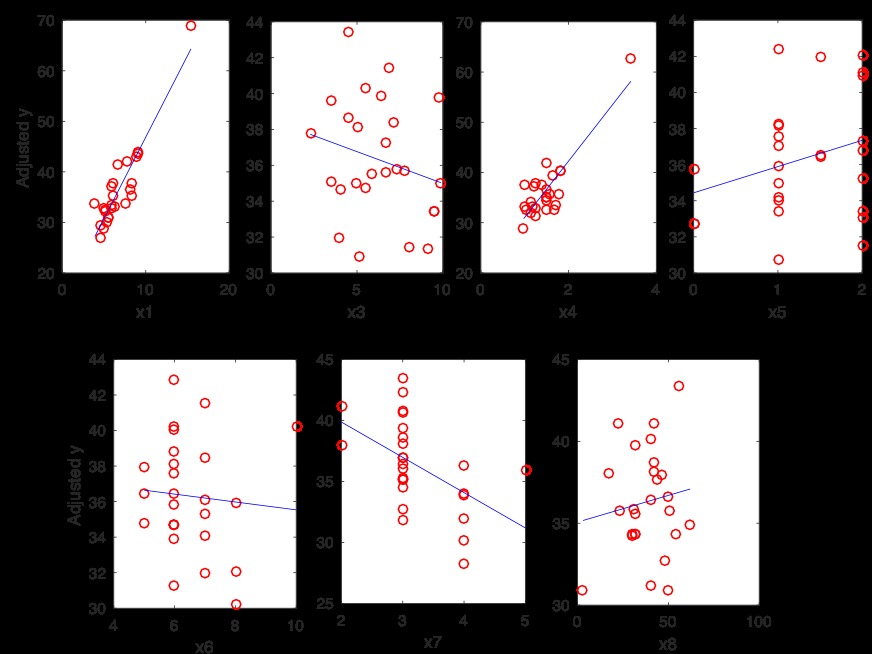
調整後的響應圖顯示擬合的響應，其他預測變量通過對擬合中使用的數據上的擬合值求平均值得到。通過將殘差加到每個觀察值的調整擬合值中來計算調整數據點。由於調整後的數據點的方差隨著x6的增加而變得越來越小，因此將x6的指數變換(而不是x6本身)添加到模型中，並在MATLAB上應用逐步回歸注釋。前向回歸的步驟如下：

COMMENT ON MATLAB
mdl7 = stepwiselm(data)

1.加x1，FStat = 192.099，pValue = 5.99118e-13

2.加x6，FStat = 12.5889，pValue = 0.00171456

3.添加x1：x6，FStat = 5.4006，pValue = 0.029761

結果模型如下：

圖14：7thModel的線性回歸結果

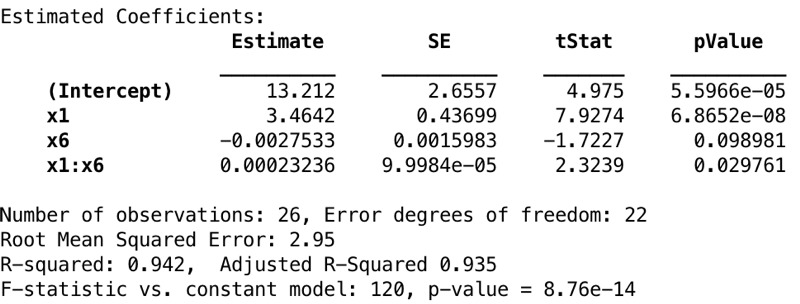
與包含x1和x4的模型進行比較時，R2和調整後的R2值顯著增加。因為x4和x6是居住麵積和房間數，所以它們是高度相關的。

模型充足性檢查

圖14顯示了beta估計值及其標準誤； t統計信息和P-values。低P-values顯示了預測變量的重要性。可以看出，模型中給出的所有預測變量都非常重要。 R2和調整後的R2值表明，該模型具有很高的解釋方差的能力。當涉及到F統計量為120時，這是很高的，構造的假設檢驗如下：

零假設：intercept-only模型與您的模型的擬合度相等。

替代假設：與您的模型相比，intercept-only模型的擬合顯著降低。

高F統計數據和低p-value顯示該模型似乎很重要。

首先要檢查模型是否合適，對殘差進行分析。殘差應呈正態分布，且無趨勢。

圖15：殘差的莖和正態概率圖

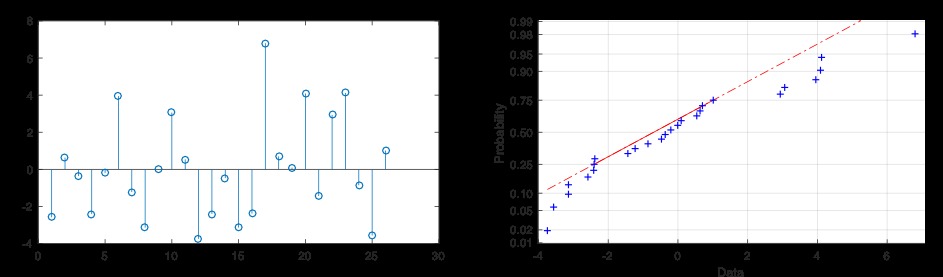
從圖15可以看出，殘差沒有任何趨勢，它們呈正態分布。正態概率圖中顯示的偏差源於數據集中的個體數量。

圖16：杠杆和Cooki距離

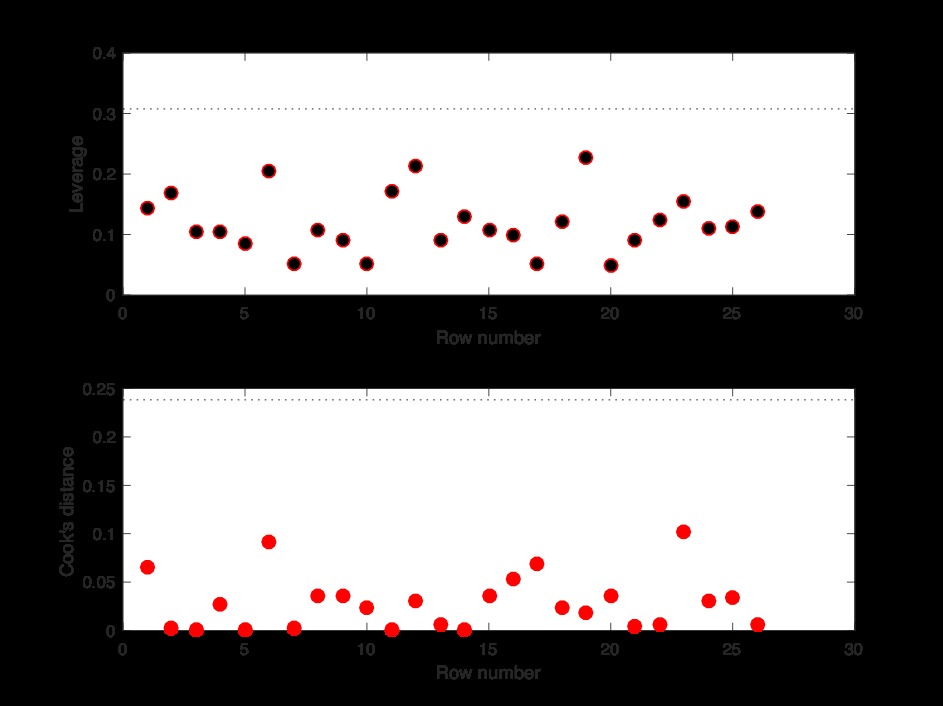
圖16顯示，數據集中不再有影響力和杠杆作用點。

結果

數據集包含對模型有重大影響的異常數據。清除異常值後，將按如下所示創建重要性模型：

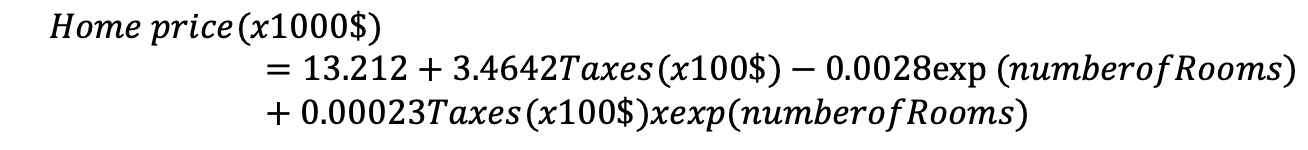
不出所料，稅收增加房屋價格上漲。另一方麵，房間數具有令人驚訝的負麵影響，但是隨著稅收的增加，由於互動條件的影響，其影響轉為正關係。房間數量的影響不是直接影響房價，而是成指數增長。

由於數據不是標準化的，因此無法相對確定影響的程度。

參考資料

本文由《純淨天空》出品。文章地址: https://vimsky.com/zh-tw/article/4593.html，未經允許，請勿轉載。