假設我們有一個數據集,如下:
import numpy as np
x = np.linspace(0,2*np.pi,100)
y = np.sin(x) + np.random.random(100) * 0.2
因此,我們的數據集有20%的變化。我的第一個想法是使用scipy的UnivariateSpline函數,但問題是這並沒有考慮到小噪聲的好處。如果考慮頻率,背景比信號小得多,所以隻有截斷的樣條可能是一個想法,但是這涉及到來回傅裏葉變換,這可能導致不良行為。另一種方式是移動平均線,但這也需要正確的延遲選擇。
有任何提示/書籍或鏈接關於如何解決這個問題的嗎?
最佳解決方法
我更喜歡Savitzky-Golay filter。它使用最小二乘法將數據的一個小窗口回歸到多項式上,然後使用多項式來估計窗口中心的點。最後窗口向前移動一個數據點,重複這個過程。這樣繼續下去,直到每個點相對於鄰居都進行了最佳調整。即使來自non-periodic(非周期)和non-linear(非線性)來源的噪音樣本也很好。
這是一個例子:thorough cookbook example。看看我的代碼,以了解它是多麽容易使用。注:我沒有定義savitzky_golay()函數的代碼,因為你可以從上麵鏈接的手冊例子中複製/粘貼它。
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0,2*np.pi,100)
y = np.sin(x) + np.random.random(100) * 0.2
yhat = savitzky_golay(y, 51, 3) # window size 51, polynomial order 3
plt.plot(x,y)
plt.plot(x,yhat, color='red')
plt.show()
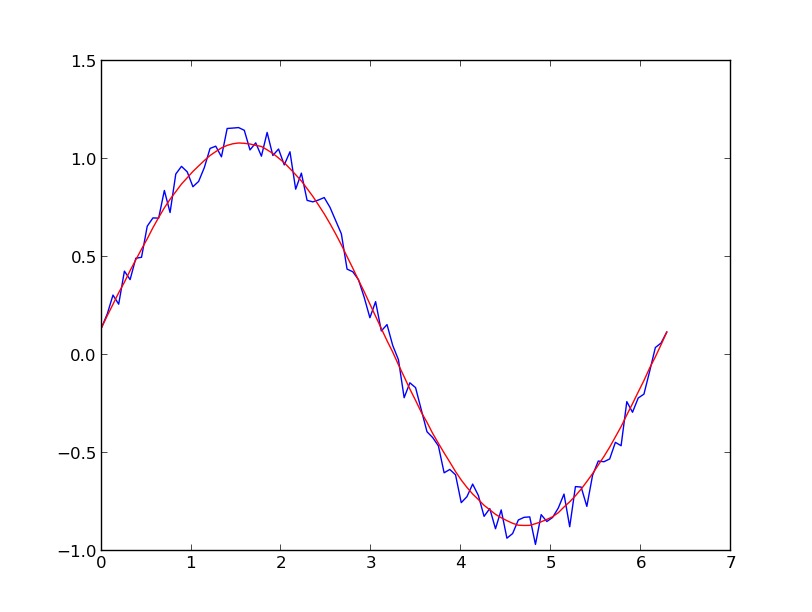
更新:我注意到,我所鏈接的例子已被刪除。幸運的是,@dodohjk指出,Savitzky-Golay過濾器已經包含在into the SciPy library中。
次佳解決方法
如果你要”smooth”版本的信號是周期性的(例如你的例子),那麽FFT是正確的選擇。進行傅裏葉變換,然後減去low-contributing頻率:
import numpy as np
import scipy.fftpack
N = 100
x = np.linspace(0,2*np.pi,N)
y = np.sin(x) + np.random.random(N) * 0.2
w = scipy.fftpack.rfft(y)
f = scipy.fftpack.rfftfreq(N, x[1]-x[0])
spectrum = w**2
cutoff_idx = spectrum < (spectrum.max()/5)
w2 = w.copy()
w2[cutoff_idx] = 0
y2 = scipy.fftpack.irfft(w2)
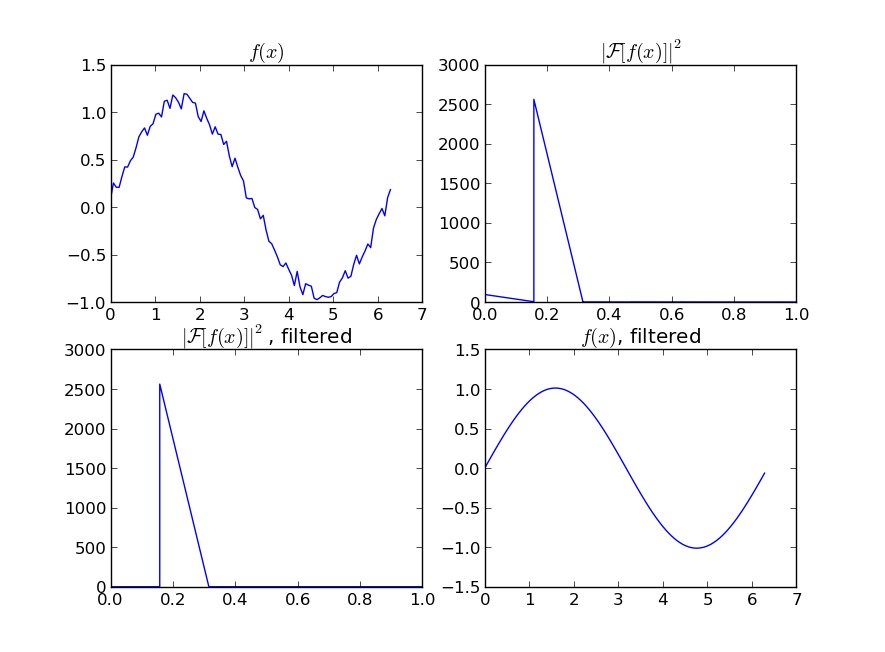
即使你的信號不完全是周期性的,這也能很好的減少白噪聲。有許多類型的過濾器可以使用(high-pass,low-pass等),適當的那個取決於你在找什麽。
第三種解決方法
一個快速和粗暴的方式來平滑我使用的數據,基於移動平均框(通過卷積):
x = np.linspace(0,2*np.pi,100)
y = np.sin(x) + np.random.random(100) * 0.8
def smooth(y, box_pts):
box = np.ones(box_pts)/box_pts
y_smooth = np.convolve(y, box, mode='same')
return y_smooth
plot(x, y,'o')
plot(x, smooth(y,3), 'r-', lw=2)
plot(x, smooth(y,19), 'g-', lw=2)
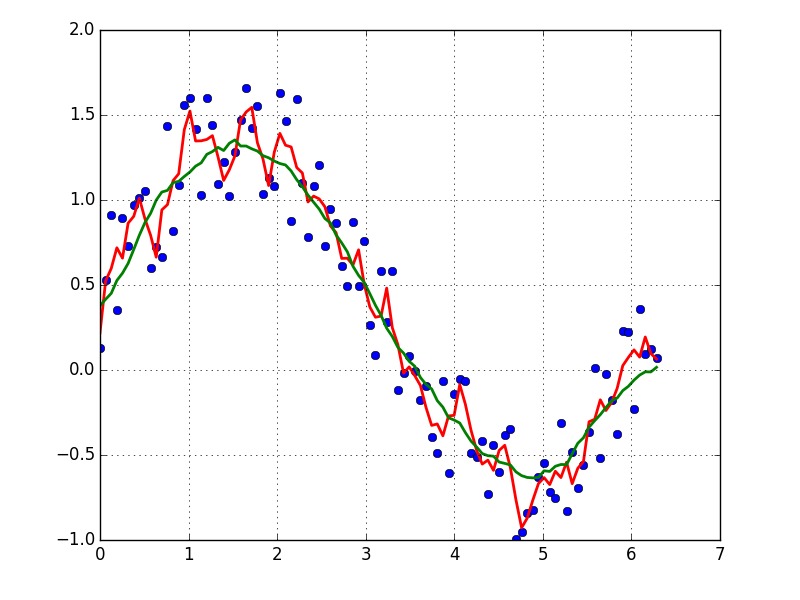
第四種方法
將移動平均值擬合到您的數據將消除噪音,請參閱this answer了解如何操作。
如果您想要使用LOWESS來擬合您的數據(它類似於移動平均數,但更複雜),您可以使用statsmodels庫來實現:
import numpy as np
import pylab as plt
import statsmodels.api as sm
x = np.linspace(0,2*np.pi,100)
y = np.sin(x) + np.random.random(100) * 0.2
lowess = sm.nonparametric.lowess(y, x, frac=0.1)
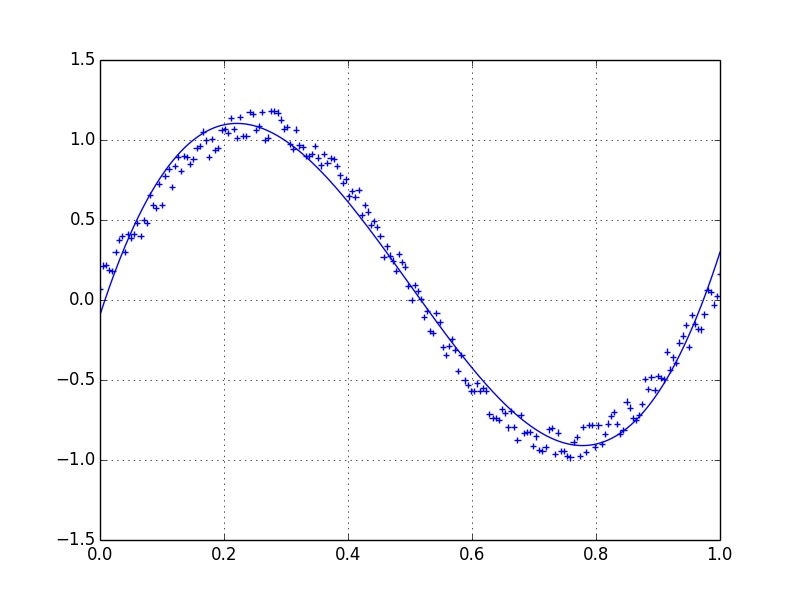
plt.plot(x, y, '+')
plt.plot(lowess[:, 0], lowess[:, 1])
plt.show()
最後,如果您知道信號的功能形式,則可以為數據擬合曲線,這可能是最好的選擇。
第五種方法
另一種選擇是在statsmodel中使用KernelReg:
from statsmodels.nonparametric.kernel_regression import KernelReg
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0,2*np.pi,100)
y = np.sin(x) + np.random.random(100) * 0.2
# The third parameter specifies the type of the variable x;
# 'c' stands for continuous
kr = KernelReg(y,x,'c')
plt.plot(x, y, '+')
y_pred, y_std = kr.fit(x)
plt.plot(x, y_pred)
plt.show()
