Python numpy random.mtrand.RandomState.laplace用法及代码示例

用法： RandomState.laplace(loc=0.0, scale=1.0, size=None)

从具有指定位置(或均值)和比例(衰减)的拉普拉斯或双 index 分布中抽取样本。

拉普拉斯分布与高斯/正态分布相似，但在峰值处更清晰，并且尾部更胖。它表示两个独立的，相同分布的 index 随机变量之间的差。

参数：

参数：	loc：： float 或 array_like of floats, 可选参数位置 $\mu$ ，分布峰值。默认值为0。 scale：： float 或 array_like of floats, 可选参数 $\lambda$ ， index 衰减。默认值为1。必须为非负数。 size：： int 或 tuple of ints, 可选参数输出形状。如果给定的形状是`(m, n, k)`，然后`m * n * k`抽取样品。如果尺寸是`None`(默认)，如果返回一个值`loc`和`scale`都是标量。除此以外，`np.broadcast(loc, scale).size`抽取样品。
返回值：	out：： ndarray或标量从参数化的拉普拉斯分布中抽取样本。

loc：： float 或 array_like of floats, 可选参数: 位置 $\mu$ ，分布峰值。默认值为0。
scale：： float 或 array_like of floats, 可选参数: $\lambda$ ， index 衰减。默认值为1。必须为非负数。
size：： int 或 tuple of ints, 可选参数: 输出形状。如果给定的形状是(m, n, k)，然后m * n * k抽取样品。如果尺寸是None(默认)，如果返回一个值loc和scale都是标量。除此以外，np.broadcast(loc, scale).size抽取样品。

返回值：

out：： ndarray或标量: 从参数化的拉普拉斯分布中抽取样本。

注意：

具有概率密度函数

$f(x; \mu, \lambda) = \frac{1}{2\lambda} \exp\left(-\frac{|x - \mu|}{\lambda}\right).$

拉普拉斯的第一定律，始于1774年，指出误差的频率可以表示为误差绝对值的 index 函数，从而得出拉普拉斯分布。对于经济学和卫生科学中的许多问题，这种分布似乎比标准的高斯分布更好地对数据建模。

参考文献：

[1]	M. Abramowitz和I.A. Stegun(编辑)。 “带有公式，图形和数学表的数学函数手册，第9次印刷”，纽约：多佛，1972年。

[2]	Kotz，Samuel等等“拉普拉斯分布与归纳”，Birkhauser，2001年。

[3]	韦斯斯坦，埃里克·W。“拉普拉斯分布”。来自MathWorld-A Wolfram Web资源。http://mathworld.wolfram.com/LaplaceDistribution.html

[4]	维基百科，“Laplace distribution”，https://en.wikipedia.org/wiki/Laplace_distribution

例子：

从分布中抽取样本

>>> loc, scale = 0., 1.
>>> s = np.random.laplace(loc, scale, 1000)

显示样本的直方图以及概率密度函数：

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 30, density=True)
>>> x = np.arange(-8., 8., .01)
>>> pdf = np.exp(-abs(x-loc)/scale)/(2.*scale)
>>> plt.plot(x, pdf)

绘制高斯以进行比较：

>>> g = (1/(scale * np.sqrt(2 * np.pi)) *
...      np.exp(-(x - loc)**2 / (2 * scale**2)))
>>> plt.plot(x,g)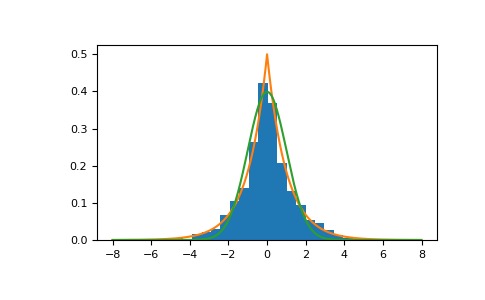

../../../_images/numpy-random-mtrand-RandomState-laplace-1.png

注：本文由纯净天空筛选整理自 numpy.random.mtrand.RandomState.laplace。非经特殊声明，原始代码版权归原作者所有，本译文未经允许或授权，请勿转载或复制。