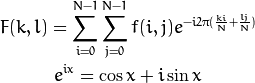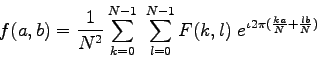在从事计算机视觉项目中，需要用到图像预处理，以帮助改善我计划构建的机器学习模型。图像预处理包括将图像滤镜应用于图像，本文将比较一些最知名的图像滤镜(也叫过滤器）。图像过滤器可用于减少图像中的噪声量并增强图像中的边。图像中可能存在两种类型的噪声：斑点噪声和胡椒盐噪声。斑点噪声是在图像采集期间产生的噪声，而胡椒盐噪声(指稀疏出现的白色和黑色像素)是由图像信号的突然干扰引起的。而增强图像的边可以帮助模型检测图像的特征。图像预处理步骤可以提高机器学习模型的准确性。与在未经预处理的图像上训练的更复杂的模型相比，经过预处理的图像可以提高基本模型的准确性。对于Python，Open-CV和PIL软件包允许您应用多个数字滤波器。应用数字滤波器涉及对图像与核(小矩阵)进行卷积。（注：核是一个n x n方阵其中n是一个奇数）。图1显示用于3 x 3平均滤波器的核。来自KDEF数据集的图像将用于数字滤波器示例。

1.均值过滤器

均值滤波器用于模糊图像以消除噪声。它涉及确定n x n核范围内像素值的平均值。然后，将中心元素的像素强度替换为平均值。这样可以消除图像中的某些噪点并平滑图像的边。 Open-CV库中的模糊函数可用于将均值滤镜应用于图像。

处理彩色图像时，首先必须将RGB转换为HSV，因为RGB的维度相互依赖，而HSV中的三个维度彼此独立(这使我们可以将滤镜分别应用于三个维度。)

以下是均值过滤器的python实现：

import numpy as np
import cv2
from matplotlib import pyplot as plt
from PIL import Image, ImageFilter
%matplotlib inline
image = cv2.imread('AM04NES.JPG') # reads the image
image = cv2.cvtColor(image, cv2.COLOR_BGR2HSV) # convert to HSV
figure_size = 9 # the dimension of the x and y axis of the kernal.
new_image = cv2.blur(image,(figure_size, figure_size))
plt.figure(figsize=(11,6))
plt.subplot(121), plt.imshow(cv2.cvtColor(image, cv2.COLOR_HSV2RGB)),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(cv2.cvtColor(new_image, cv2.COLOR_HSV2RGB)),plt.title('Mean filter')
plt.xticks([]), plt.yticks([])
plt.show()

图2显示，虽然减少了一些斑点噪声，但是图像中现在存在许多以前不存在的伪影像。我们可以检查将均值滤镜应用于灰度图像时是否创建了伪像。

# The image will first be converted to grayscale
image2 = cv2.cvtColor(image, cv2.COLOR_HSV2BGR)
image2 = cv2.cvtColor(image2, cv2.COLOR_BGR2GRAY)
figure_size = 9
new_image = cv2.blur(image2,(figure_size, figure_size))
plt.figure(figsize=(11,6))
plt.subplot(121), plt.imshow(image2, cmap='gray'),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(new_image, cmap='gray'),plt.title('Mean filter')
plt.xticks([]), plt.yticks([])
plt.show()

图3显示，均值滤波可以消除一些噪声，并且不会在灰度图像上产生伪影像。但是，一些细节已丢失。

2.高斯滤波器

高斯滤波器类似于均值滤波器，但是它涉及周围像素的加权平均值，并具有参数sigma。核代表高斯分布的离散近似。尽管高斯滤镜也会使图像的边模糊(如均值滤镜)，但与相似大小的均值滤镜相比，它在保留边方面做得更好。 Open-CV软件包中的“ GaussianBlur”功能可用于实现高斯滤波器。该函数允许您指定核的形状。还可以分别指定x和y方向的标准偏差。如果仅指定一个西格玛值(sigma, σ)，则将其视为x和y方向共享的西格玛值。

new_image = cv2.GaussianBlur(image, (figure_size, figure_size),0)
plt.figure(figsize=(11,6))
plt.subplot(121), plt.imshow(cv2.cvtColor(image, cv2.COLOR_HSV2RGB)),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(cv2.cvtColor(new_image, cv2.COLOR_HSV2RGB)),plt.title('Gaussian Filter')
plt.xticks([]), plt.yticks([])
plt.show()

图4显示，与均值滤波器相比，高斯滤波器在保留图像边方面做得更好，但是在彩色图像上也会产生伪像。现在我们可以检查高斯滤波器是否在灰度图像上产生伪像。

new_image_gauss = cv2.GaussianBlur(image2, (figure_size, figure_size),0)
plt.figure(figsize=(11,6))
plt.subplot(121), plt.imshow(image2, cmap='gray'),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(new_image_gauss, cmap='gray'),plt.title('Gaussian Filter')
plt.xticks([]), plt.yticks([])
plt.show()

图5显示了将9 x 9高斯滤波器应用于灰度图像时不会产生伪像。该滤镜比9 x 9的平均滤镜可以保留更多细节，并可以消除一些噪音。

3.中值过滤器

中值过滤器计算n x n核内围绕像素中心像素的像素强度的中值。然后，用该中位数替换中心像素的像素强度。中值滤波器比平均值滤波器和高斯滤波器在消除胡椒盐噪声方面做得更好。中值滤镜保留图像的边，但不处理斑点噪声。 Open-CV库中的“ medianBlur”功能可用于实现中值滤波器。

new_image = cv2.medianBlur(image, figure_size)
plt.figure(figsize=(11,6))
plt.subplot(121), plt.imshow(cv2.cvtColor(image, cv2.COLOR_HSV2RGB)),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(cv2.cvtColor(new_image, cv2.COLOR_HSV2RGB)),plt.title('Median Filter')
plt.xticks([]), plt.yticks([])
plt.show()

图6显示，中值滤波器能够保留图像的边，同时消除胡椒盐噪声。与均值和高斯滤波器不同，中值滤波器不会在彩色图像上产生伪像。接下来，中值滤镜将应用于灰度图像。

new_image = cv2.medianBlur(image2, figure_size)
plt.figure(figsize=(11,6))
plt.subplot(121), plt.imshow(image2, cmap='gray'),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(new_image, cmap='gray'),plt.title('Median Filter')
plt.xticks([]), plt.yticks([])
plt.show()

图7显示了一个9 x 9的中值滤镜可以在保留图像边的同时消除一些胡椒盐噪声。

其他过滤器：

以下是另外一些可用于图像预处理的过滤器：

保守过滤器/最值滤波器

保守过滤器用于去除胡椒盐噪音。确定像素附近的最小强度和最大强度。如果中心像素的强度大于最大值，则将其替换为最大值。如果小于最小值，则将其替换为最小值。保守滤镜可以保留边，但不能消除斑点噪声。

以下代码可用于定义保守过滤器：

# first a conservative filter for grayscale images will be defined.
def conservative_smoothing_gray(data, filter_size):
temp = []
    
    indexer = filter_size // 2
    
    new_image = data.copy()
    
    nrow, ncol = data.shape
    
    for i in range(nrow):
        
        for j in range(ncol):
            
            for k in range(i-indexer, i+indexer+1):
                
                for m in range(j-indexer, j+indexer+1):
                    
                    if (k > -1) and (k < nrow): if (m > -1) and (m < ncol): temp.append(data[k,m]) temp.remove(data[i,j]) max_value = max(temp) min_value = min(temp) if data[i,j] > max_value:
                
                new_image[i,j] = max_value
            
            elif data[i,j] < min_value:
                
                new_image[i,j] = min_value
            
            temp =[]
    
    return new_image.copy()

现在，可以将保守滤镜应用于灰度图像：

new_image = conservative_smoothing_gray(image2,5)
plt.figure(figsize=(11,6))
plt.subplot(121), plt.imshow(image2, cmap='gray'),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(122), plt.imshow(new_image, cmap='gray'),plt.title('Conservative Smoothing')
plt.xticks([]), plt.yticks([])
plt.show()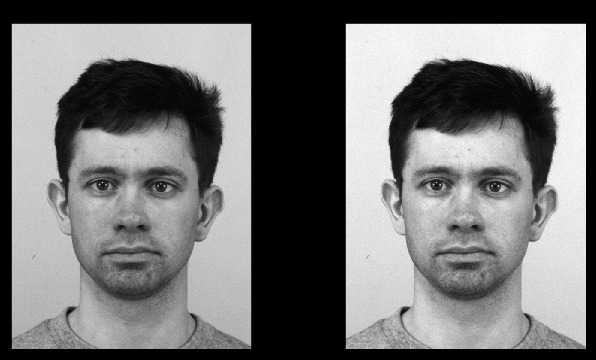

图9表明，保守平滑滤波器能够消除一些胡椒盐噪声。但该滤波器无法像中值滤波器一样消除更多胡椒盐噪声(尽管它确实保留了更多细节)。

拉普拉斯过滤器

图像的拉普拉斯算子突出显示强度快速变化的区域，因此可以用于边检测。如果我们让I(x，y)表示图像的强度，则图像的拉普拉斯算子由以下公式给出：

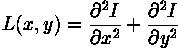
拉普拉斯算子在特定像素处的离散近似值可以通过在像素的小邻域中采用像素强度的加权平均值来确定。图10显示了两个核，它们代表了逼近拉普拉斯算子的两种不同方式。

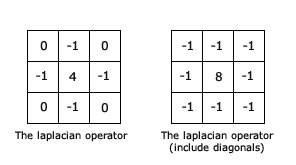
由于拉普拉斯滤镜检测图像的边，因此可以将其与高斯滤镜一起使用，以便首先去除斑点噪声，然后突出显示图像的边。此方法称为拉普拉斯高斯滤波。 Open-CV库中的“拉普拉斯算子”功能可用于查找图像的拉普拉斯算子。

new_image = cv2.Laplacian(image2,cv2.CV_64F)
plt.figure(figsize=(11,6))
plt.subplot(131), plt.imshow(image2, cmap='gray'),plt.title('Original')
plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.imshow(new_image, cmap='gray'),plt.title('Laplacian')
plt.xticks([]), plt.yticks([])
plt.subplot(133), plt.imshow(image2 + new_image, cmap='gray'),plt.title('Resulting image')
plt.xticks([]), plt.yticks([])
plt.show()

图11显示，虽然将图像的拉普拉斯算子添加到原始图像可能会增强边，但也会增加一些噪点。

频率滤波器

在将频率滤波器应用于图像时，重要的是首先将图像转换为图像的频域表示。傅里叶变换(将一个函数分解成其正弦和余弦分量)可以应用于图像，以获得其频域表示。我们对图像的频域表示感兴趣的原因是，在频域中对图像应用频率滤波器要比在空间域中应用滤波器更方便。这是基于以下事实：频域表示中的每个像素都对应于一个频率而不是图像的位置。

低通滤波器和高通滤波器都是频率滤波器。低通滤波器保留最低频率(低于阈值)，这意味着它会模糊边并从空间域中的图像中去除斑点噪声。高通滤波器可以保留高频，这意味着可以保留边。 “ dft”功能确定图像的离散傅立叶变换。为一个N x N图像做二维离散傅里叶变换由下式给出：

其中，f是空间域中的图像值，F是其频域中的图像值。以下是离散傅立叶逆变换的公式(它将图像从频域转换到空间域)：

一旦将频率滤波器应用于图像之后，就可以使用傅立叶逆变换将图像转换回空间域。现在将给出低通滤波器的python实现：

dft = cv2.dft(np.float32(image2),flags = cv2.DFT_COMPLEX_OUTPUT)
# shift the zero-frequncy component to the center of the spectrum
dft_shift = np.fft.fftshift(dft)
# save image of the image in the fourier domain.
magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
# plot both images
plt.figure(figsize=(11,6))
plt.subplot(121),plt.imshow(image2, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

rows, cols = image2.shape
crow,ccol = rows//2 , cols//2
# create a mask first, center square is 1, remaining all zeros
mask = np.zeros((rows,cols,2),np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1
# apply mask and inverse DFT
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv2.idft(f_ishift)
img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1])
# plot both images
plt.figure(figsize=(11,6))
plt.subplot(121),plt.imshow(image2, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
plt.title('Low Pass Filter'), plt.xticks([]), plt.yticks([])
plt.show()

图13显示丢失了很多细节，但是去除了一些斑点噪声。

Crimmin去除斑点

Crimmins互补剔除算法用于去除斑点噪声并平滑边。它还可以降低胡椒盐噪声的强度。该算法将图像中像素的强度与其8个相邻像素的强度进行比较。该算法考虑4组邻居(N-S，E-W，NW-SE，NE-SW)。假设a，b，c是三个连续像素(例如来自E-S)。那么算法是：

对于每次迭代：
a)暗像素调整：针对四个方向中的每个方向
1)使用以下方法处理整个图像：if a ≥ b+2 then b = b + 1
2)使用以下方法处理整个图像：if a > b and b ≤ c then b = b + 1
3)使用以下方法处理整个图像：if c > b and b ≤ a then b = b + 1
4)使用以下方法处理整个图像：if c ≥ b+2 then b = b + 1
b)亮像素调整：针对四个方向的每个方向
1)使用以下方法处理整个图像： if a ≤ b — 2 then b = b — 1
2)使用以下方法处理整个图像：if a < b and b ≥ c then b = b — 1
3)使用以下方法处理整个图像：if c < b and b ≥ a then b = b — 1
4)使用以下方法处理整个图像：if c ≤ b — 2 then b = b — 1

可以在此处找到互补剔除算法的Python实现。

图14显示了将Crimmins斑点去除滤镜应用于图像的结果。去除了一些斑点噪声，但是一些边变得模糊。

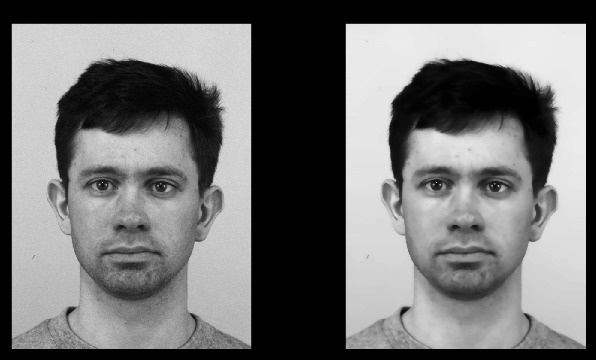
锐化滤镜

锐化滤镜可用于增强图像的边。 PIL包中的ImageFilter.Unsharpmask函数将锐化滤镜应用于图像(注：首先需要将图像转换为PIL Image对象）。ImageFilter.Unsharpmask函数具有三个参数。 “radius”参数指定边周围有多少相邻像素受到影响。 “percentage”参数指定边变暗或变亮的程度。第三个参数“threshold”定义在滤波器执行任何操作之前相邻色调值必须相距多远。

image = Image.fromarray(image.astype('uint8'))
new_image = image.filter(ImageFilter.UnsharpMask(radius=2, percent=150))
plt.subplot(121),plt.imshow(image, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(new_image, cmap = 'gray')
plt.title('Unsharp Filter'), plt.xticks([]), plt.yticks([])
plt.show()

图15显示了Unsharp滤镜的结果。在增强图像边的同时，也增强了一些噪点。

结论

在消除噪点和保留图像边之间始终需要权衡取舍。为了消除图像中的斑点噪声，需要应用模糊滤波器，该滤波器又使图像的边模糊。如果要保留图像的边，则唯一可以消除的噪声是胡椒盐噪声。可以在此处找到Jupyter Notebook以及本文使用的所有代码：https://github.com/m4nv1r/medium_articles/blob/master/Image_Filters_in_Python.ipynb

参考资料

Image Filters in Python