汉诺塔(hanoi)递归实现的图示化（原创）

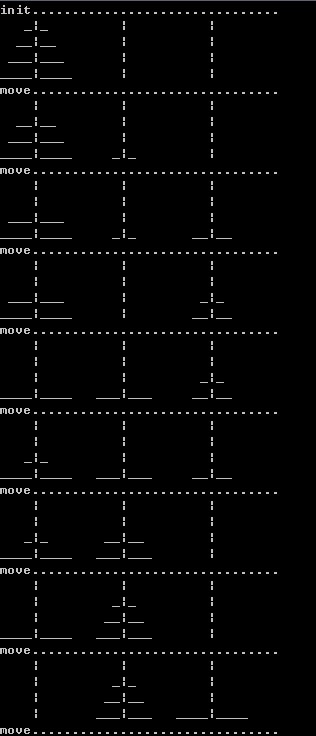
Hanoi Tower，也叫汉诺塔、河内之塔、汉罗塔等，是如下图(来自百度图片)所示的一个游戏：

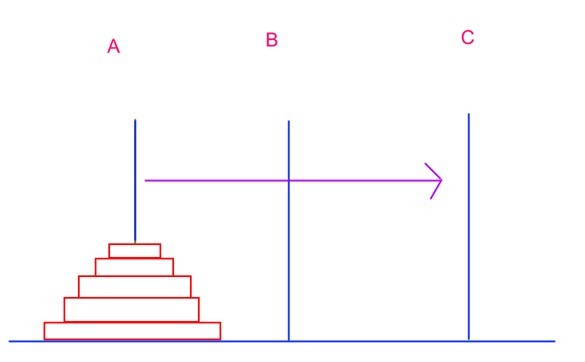
要求将塔A的盘全部移到C，移动过程中不能将大盘放到小盘的上面。
Hanoi Tower的递归算法实现思想为(假设盘数为N)
1）当A只有一个盘时(即N = 1)，直接将盘移动到C
2）当A中有两个或者两个以上的盘时(即N >=2)，
先递归地将N-1个盘从塔A移到辅助塔B，
再将剩下的一个盘从塔A移到塔C
最后递归地将N-1个盘从塔B移到塔C
递归实现的核心代码如下：

hanoi_move( int n, int x, int y, int z )
{

    if( n==1 )
        printf( "%c-->%c\n", x, z );//从X移到Z
    else
    {
        hanoi_move( n-1, x, z, y);//n-1个盘从X移到Y，Z为辅助

        printf( "%c-->%c\n", x, z );//1个盘从x移到Z

        hanoi_move( n-1, y, x, z );//n-1个盘从Y移到Z，X为辅助
    }
}

上面的代码虽然简单，但是递归的过程并不容易理解，本文旨在于将递归过程的每一步移动用简单图形的方式
展现出来。以下是在VC++ 6.0 编译器中实现的可图示化Hanoi Tower的执行过程的源代码（C++）

#include 
#include 
using namespace std;

//hanoi tower
vector A; //Tower A
vector B;//Tower B
vector C; //Tower C
int N; //The number of plates

//initialize the towers=====================================
void init()
{
    cout<<"init..............................."<<endl; int i; for(i = N; i >= 1; --i)
        A.push_back(i);
    B.clear();
    C.clear();
}

//print towers using characters=============================
void print_char(int n, char ch)
{
    int i;
    for(i = 0; i < n; ++i)
        cout<<ch; } void print_plate(int n) { print_char(N - n, ' '); print_char(n, '_'); print_char(1, '|'); print_char(n, '_'); print_char(N -n, ' '); } void print_empty() { print_char(N, ' '); print_char(1, '|'); print_char(N, ' '); } void print_tower() { int i; for(i = N - 1; i >= 0; --i)
    {
        if(i < A.size())
            print_plate(A[i]);
        else
            print_empty();
        cout<<"  ";

        if(i < B.size())
            print_plate(B[i]);
        else
            print_empty();
        cout<<"  ";

        if(i < C.size())
            print_plate(C[i]);
        else
            print_empty();

        cout<<endl;

    }
}

//hanoi algorithom================================================
void move(vector& x, vector& y)
{
    cout<<"move..............................."<<endl;
    int temp = x.back();
    x.pop_back();
    y.push_back(temp);
    print_tower();
}

void hanoi(int n, vector& a, vector& b, vector& c)
{
    if(n == 1)
    {
        move(a, c);
    }
    else
    {
        hanoi(n - 1, a, c, b);//moving the n-1 plates from a to b
        move(a, c); //move a plate from a to c
        hanoi(n - 1, b, a, c);//moving the n-1 plates from b to c
    }
}

//main =============================================================
int main()
{

    N = 4;
    init();
    print_tower();
    hanoi(N, A, B, C);
    system("pause");
    return 0;
}

运行结果如下(由于运行结果较长，下面有两张图片一起展示运行结果）：