一般的二叉搜索树(BST)在插入和删除数据的时候,直接在一定的位置添加和删除节点,没有应用使树
平衡的调整策略,树的高度不能得到有效控制,在极端的数据下可能退化为单链表从而降低二叉搜索树的性能。为了
使二叉搜索树更具有通用性,出现了AVL树和红黑树这两种平衡二叉树,它们增、删、查和普通的BST一致,但是使用
了四种基本的策略来保持树的平衡,从而保证较高的查询效率。这四种调整策略是LL调整、RR调整、LR调整、RL调整,
其中LL调整和RR调整对称,LR调整和RL调整对称。下面使用图形来展示这四种二叉搜索树的平衡调整策略。
一、LL调整。如图1所示,单向右旋,使A的左儿子B成为A的父节点。
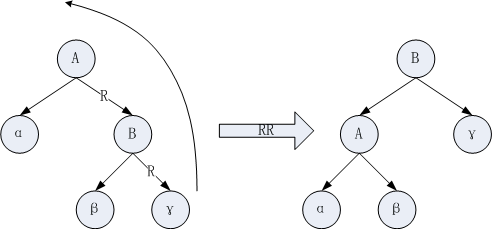
二、RR调整。如图2所示,单向左旋,使A的右儿子B成为A的父亲节点。
三、LR调整。如图3所示,先左旋后右旋,即,现将A的左儿子B的右儿子C单向左旋,使C成为B的父节点,然后将C单向右旋成为A的父节点
四、RL调整。如果4所示,先右旋后左旋,即,现将A的右儿子B的左儿子C单向右旋,使C成为B的父节点,然后将C单向左旋成为A的父节点。
参考文献:《数据结构教程(第二版)》清华大学出版社