這些函數可用於生成監督(分類和回歸)和無監督建模應用程序的模擬數據。
用法
sim_classification(
num_samples = 100,
method = "caret",
intercept = -5,
num_linear = 10,
keep_truth = FALSE
)
sim_regression(
num_samples = 100,
method = "sapp_2014_1",
std_dev = NULL,
factors = FALSE,
keep_truth = FALSE
)
sim_noise(
num_samples,
num_vars,
cov_type = "exchangeable",
outcome = "none",
num_classes = 2,
cov_param = 0
)
sim_logistic(num_samples, eqn, correlation = 0, keep_truth = FALSE)
sim_multinomial(
num_samples,
eqn_1,
eqn_2,
eqn_3,
correlation = 0,
keep_truth = FALSE
)參數
- num_samples
-
要模擬的數據點的數量。
- method
-
模擬方法的字符串。對於分類，當前的單個選項是"caret"。對於回歸，值可以是 "sapp_2014_1"、"sapp_2014_2"、"van_der_laan_2007_1" 或 "van_der_laan_2007_2"。請參閱下麵的詳細信息。
- intercept
-
線性預測器的截距。
- num_linear
-
線性遞減效應的數量。
- keep_truth
-
邏輯：是否應該保留數據的真實結果值？如果是這樣，則列名稱為
.truth。 - std_dev
-
殘差的高斯分布標準差。默認值顯示在下麵的詳細信息中。
- factors
-
用於確定二進製指標是否應編碼為因子的單一邏輯。
- num_vars
-
要創建的噪聲預測器的數量。
- cov_type
-
預測變量的多元正態相關結構。可能的值為"exchangeable" 和"toeplitz"。
- outcome
-
應模擬什麽類型的獨立結果(如果有)的單個字符串。 "none" 的默認值不會產生額外的列。使用"classification" 將生成一個
class列，其中包含均勻分布的num_classes值。 "regression" 值會生成包含獨立標準正常值的outcome列。 - num_classes
-
當
outcome = "classification"時，要模擬的類的數量。 - cov_param
-
可交換相關值或托普利茨結構的基礎的單個數值。請參閱下麵的詳細信息。
- eqn, eqn_1, eqn_2, eqn_3
-
僅涉及用於計算線性預測變量的變量
A和B的 R 表達式或(單邊)公式。外部物體不應用作符號；請參閱下麵的示例，了解如何在方程中使用外部對象。 - correlation
-
變量
A和B之間相關性的單個數值。
細節
具體回歸和分類方法
這些函數提供了幾種有監督的模擬方法(和一種無監督的)。通過 method 了解更多信息：
method = "caret"
這是一個具有兩個類的模擬分類問題，最初是在 caret::twoClassSim() 中使用所有數字預測變量實現的。預測變量在不同的集合中進行模擬。首先，創建相關性約為 0.65 的兩個多元正態預測變量(此處表示為 two_factor_1 和 two_factor_2 )。他們使用主效應和交互來改變log-odds：
intercept - 4 * two_factor_1 + 4 * two_factor_2 + 2 * two_factor_1 * two_factor_2 截距是模擬的一個參數，可用於控製類不平衡量。
第二組效應與交替符號的係數呈線性關係，並且具有 2.5 和 0.25 之間的一係列值。例如，如果該集合中有四個預測變量，則它們對 log-odds 的貢獻將為
-2.5 * linear_1 + 1.75 * linear_2 -1.00 * linear_3 + 0.25 * linear_4(請注意，這些列名稱可能會根據 num_linear 的值而更改)。
第三組是單個預測器的非線性函數，範圍在[0, 1]之間，此處稱為non_linear_1：
(non_linear_1^3) + 2 * exp(-6 * (non_linear_1 - 0.3)^2) 第四組信息預測變量是從 Friedman 的一個係統複製的，並使用另外兩個預測變量( non_linear_2 和 non_linear_3 )：
2 * sin(non_linear_2 * non_linear_3) 所有這些效果相加後就形成了 log-odds 模型。
method = "sapp_2014_1"
該回歸模擬來自 Sapp 等人。 (2014)。有 20 個獨立的高斯隨機預測變量，均值為零，方差為 9。預測方程為：
predictor_01 + sin(predictor_02) + log(abs(predictor_03)) +
predictor_04^2 + predictor_05 * predictor_06 +
ifelse(predictor_07 * predictor_08 * predictor_09 < 0, 1, 0) +
ifelse(predictor_10 > 0, 1, 0) + predictor_11 * ifelse(predictor_11 > 0, 1, 0) +
sqrt(abs(predictor_12)) + cos(predictor_13) + 2 * predictor_14 + abs(predictor_15) +
ifelse(predictor_16 < -1, 1, 0) + predictor_17 * ifelse(predictor_17 < -1, 1, 0) -
2 * predictor_18 - predictor_19 * predictor_20誤差為高斯分布，均值為零，方差為 9。
method = "sapp_2014_2"
該回歸模擬也來自 Sapp 等人。 (2014)。有 200 個獨立的高斯預測變量，均值為零，方差為 16。預測方程的截距為 1，且線性效應與 log(abs(predictor)) 相同。
誤差為高斯分布，均值為零，方差為 25。
method = "van_der_laan_2007_1"
這是 van der Laan 等人的回歸模擬。 (2007) 有 10 個隨機伯努利變量，其值為 1 的概率為 40%。真實的回歸方程為：
2 * predictor_01 * predictor_10 + 4 * predictor_02 * predictor_07 +
3 * predictor_04 * predictor_05 - 5 * predictor_06 * predictor_10 +
3 * predictor_08 * predictor_09 + predictor_01 * predictor_02 * predictor_04 -
2 * predictor_07 * (1 - predictor_06) * predictor_02 * predictor_09 -
4 * (1 - predictor_10) * predictor_01 * (1 - predictor_04)誤差項為標準正態。
method = "van_der_laan_2007_2"
這是 van der Laan 等人的另一個回歸模擬。 (2007)，二十個高斯分布，均值為零，方差為 16。預測方程為：
predictor_01 * predictor_02 + predictor_10^2 - predictor_03 * predictor_17 -
predictor_15 * predictor_04 + predictor_09 * predictor_05 + predictor_19 -
predictor_20^2 + predictor_09 * predictor_08誤差項也是高斯分布，均值為零，方差為 16。
method = "hooker_2004"
Hooker (2004) 和 Sorokina at al (2008) 使用了以下內容：
pi ^ (predictor_01 * predictor_02) * sqrt( 2 * predictor_03 ) -
asin(predictor_04) + log(predictor_03 + predictor_05) -
(predictor_09 / predictor_10) * sqrt (predictor_07 / predictor_08) -
predictor_02 * predictor_07預測變量 1、2、3、6、7 和 9 是標準統一的，而其他預測變量在 [0.6, 1.0] 上是統一的。誤差是正常的，平均值為零，默認標準差為 0.25。
sim_noise()
該函數模擬多個均值為零的隨機正態變量。如果 cov_param = 0 ，這些值可以是獨立的。否則，這些值是具有非對角協方差矩陣的多元正態分布。對於 cov_type = "exchangeable" ，該結構具有 cov_param 的單位方差和協方差。對於 cov_type = "toeplitz" ，協方差具有指數模式(請參見下麵的示例)。
物流模擬
sim_logistic() 提供了一個靈活的接口，用於模擬具有兩個多元正態變量 A 和 B 的邏輯回歸模型(均值為零、單位方差和相關性由 correlation 參數確定)。
例如，使用 eqn = A + B 將指定事件的真實概率為
prob = 1 / (1 + exp(A + B))結果列的類級別為 "one" 和 "two" 。
多項式模擬
sim_multinomial() 可以根據參數 eqn_1 、 eqn_2 和 eqn_3 中的值分別生成類 "one" 、 "two" 和 "three" 的數據。與 sim_logistic() 一樣，這些方程使用預測變量 A 和 B 。
對各個方程進行求值和求冪。此後，對於每行數據，它們的值將被歸一化以加起來為 1。這些概率被傳遞給 stats::rmultinom() 以生成結果值。
參考
Van der Laan, M. J.、Polley, E. C. 和 Hubbard, A. E. (2007)。超級學習者。遺傳學和分子生物學中的統計應用，6(1)。 DOI：10.2202/1544-6115.1309。
Sapp, S.、van der Laan, M. J. 和 Canny, J. (2014)。 Subsemble：一種結合subset-specific算法擬合的集成方法。應用統計學雜誌，41(6), 1247-1259。 DOI：10.1080/02664763.2013.864263
胡克，G.(2004 年 8 月)。發現黑盒函數中的加性結構。第十屆 ACM SIGKDD 知識發現和數據挖掘國際會議論文集(第 575-580 頁)。數字編號：10.1145/1014052.1014122
Sorokina, D.、Caruana, R.、Riedewald, M. 和 Fink, D.(2008 年 7 月)。檢測與附加樹林的統計相互作用。第 25 屆國際機器學習會議論文集(第 1000-1007 頁)。數字編號：10.1145/1390156.1390282
例子
set.seed(1)
sim_regression(100)
#> # A tibble: 100 × 21
#> outcome predictor_01 predictor_02 predictor_03 predictor_04
#> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 8.49 -1.88 -1.86 1.23 2.68
#> 2 19.3 0.551 0.126 5.07 -3.14
#> 3 57.7 -2.51 -2.73 4.76 5.91
#> 4 -8.41 4.79 0.474 -0.993 -1.15
#> 5 43.0 0.989 -1.96 -6.86 4.96
#> 6 72.3 -2.46 5.30 7.49 4.54
#> 7 -3.36 1.46 2.15 2.00 0.249
#> 8 -3.82 2.21 2.73 1.62 1.70
#> 9 22.7 1.73 1.15 -0.0402 -3.07
#> 10 25.7 -0.916 5.05 1.53 0.969
#> # ℹ 90 more rows
#> # ℹ 16 more variables: predictor_05 <dbl>, predictor_06 <dbl>,
#> # predictor_07 <dbl>, predictor_08 <dbl>, predictor_09 <dbl>,
#> # predictor_10 <dbl>, predictor_11 <dbl>, predictor_12 <dbl>,
#> # predictor_13 <dbl>, predictor_14 <dbl>, predictor_15 <dbl>,
#> # predictor_16 <dbl>, predictor_17 <dbl>, predictor_18 <dbl>,
#> # predictor_19 <dbl>, predictor_20 <dbl>
sim_classification(100)
#> # A tibble: 100 × 16
#> class two_factor_1 two_factor_2 non_linear_1 non_linear_2 non_linear_3
#> <fct> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 class… -2.27 -1.18 -0.245 0.888 0.354
#> 2 class… -0.537 0.420 0.621 0.170 0.374
#> 3 class… 3.23 2.39 0.163 0.957 0.840
#> 4 class… 3.42 0.236 0.110 0.788 0.134
#> 5 class… 0.571 -0.100 -0.487 0.377 0.541
#> 6 class… -1.61 -0.0701 0.393 0.789 0.515
#> 7 class… 2.74 2.51 -0.751 0.459 0.931
#> 8 class… 0.0763 -0.679 0.307 0.220 0.771
#> 9 class… 0.0591 -2.35 0.402 0.566 0.712
#> 10 class… -1.39 -2.10 -0.887 0.0154 0.0784
#> # ℹ 90 more rows
#> # ℹ 10 more variables: linear_01 <dbl>, linear_02 <dbl>, linear_03 <dbl>,
#> # linear_04 <dbl>, linear_05 <dbl>, linear_06 <dbl>, linear_07 <dbl>,
#> # linear_08 <dbl>, linear_09 <dbl>, linear_10 <dbl>
# Flexible logistic regression simulation
if (rlang::is_installed("ggplot2")) {
library(dplyr)
library(ggplot2)
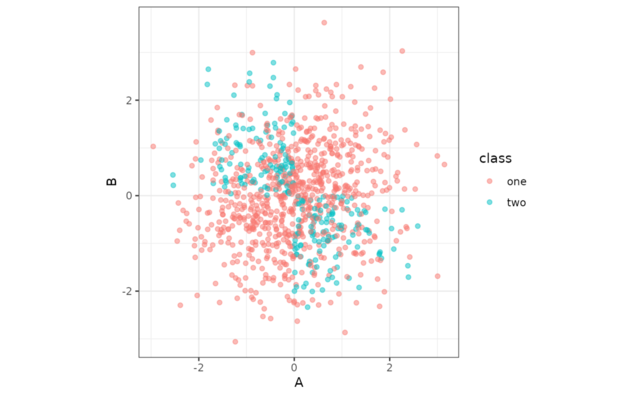
sim_logistic(1000, ~ .1 + 2 * A - 3 * B + 1 * A *B, corr = .7) %>%
ggplot(aes(A, B, col = class)) +
geom_point(alpha = 1/2) +
coord_equal()
f_xor <- ~ 10 * xor(A > 0, B < 0)
# or
f_xor <- rlang::expr(10 * xor(A > 0, B < 0))
sim_logistic(1000, f_xor, keep_truth = TRUE) %>%
ggplot(aes(A, B, col = class)) +
geom_point(alpha = 1/2) +
coord_equal() +
theme_bw()
}
#>
#> Attaching package: ‘dplyr’
#> The following objects are masked from ‘package:stats’:
#>
#> filter, lag
#> The following objects are masked from ‘package:base’:
#>
#> intersect, setdiff, setequal, union
## How to use external symbols:
a_coef <- 2
# splice the value in using rlang's !! operator
lp_eqn <- rlang::expr(!!a_coef * A+B)
lp_eqn
#> 2 * A + B
sim_logistic(5, lp_eqn)
#> # A tibble: 5 × 3
#> A B class
#> <dbl> <dbl> <fct>
#> 1 -0.315 0.990 one
#> 2 0.964 -0.0664 one
#> 3 1.16 0.258 one
#> 4 1.09 -0.621 one
#> 5 2.65 -0.776 one
# Flexible multinomial regression simulation
if (rlang::is_installed("ggplot2")) {
}
#> NULL
相關用法
- R modelr typical 求典型值
- R modelr resample “惰性”重采樣。
- R modelr crossv_mc 生成測試訓練對以進行交叉驗證
- R modelr model_matrix 構建設計矩陣
- R modelr model-quality 計算給定數據集的模型質量
- R modelr permute 生成 n 個排列重複。
- R modelr fit_with 擬合公式列表
- R modelr add_residuals 將殘差添加到 DataFrame
- R modelr data_grid 生成數據網格。
- R modelr formulas 創建公式列表
- R modelr add_predictions 將預測添加到 DataFrame
- R modelr seq_range 生成向量範圍內的序列
- R modelr resample_partition 生成數據幀的獨占分區
- R modelr add_predictors 將預測變量添加到公式中
- R modelr na.warn 處理缺失值並發出警告
- R modelr bootstrap 生成 n 個引導程序重複。
- R modelr resample_bootstrap 生成 boostrap 複製
- R vcov.gam 從 GAM 擬合中提取參數(估計器)協方差矩陣
- R gam.check 擬合 gam 模型的一些診斷
- R matrix轉list用法及代碼示例
- R as 強製對象屬於某個類
- R null.space.dimension TPRS 未懲罰函數空間的基礎
- R language-class 表示未評估語言對象的類
- R gam.reparam 尋找平方根懲罰的穩定正交重新參數化。
- R className 類名包含對應的包
注：本文由純淨天空篩選整理自Max Kuhn等大神的英文原創作品 Simulate datasets。非經特殊聲明，原始代碼版權歸原作者所有，本譯文未經允許或授權，請勿轉載或複製。