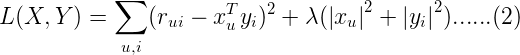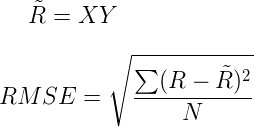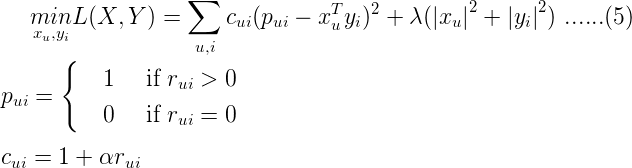協同過濾之ALS-WR算法

這篇文章是參考：https://github.com/ceys/jdml/wiki/ALS 改寫的，由於原文Latex公式沒有正常展現+少量筆誤，妨礙閱讀，所以這裏重新整理了一下。

ALS是alternating least squares的縮寫 , 意為交替最小二乘法；而ALS-WR是alternating-least-squares with weighted-λ -regularization的縮寫，意為加權正則化交替最小二乘法。該方法常用於基於矩陣分解的推薦係統中。例如：將用戶(user)對商品(item)的評分矩陣分解為兩個矩陣：一個是用戶對商品隱含特征的偏好矩陣，另一個是商品所包含的隱含特征的矩陣。在這個矩陣分解的過程中，評分缺失項得到了填充，也就是說我們可以基於這個填充的評分來給用戶最商品推薦了。

ALS

由於評分數據中有大量的缺失項，傳統的矩陣分解SVD（奇異值分解）不方便處理這個問題，而ALS能夠很好的解決這個問題。對於R(m×n)的矩陣，ALS旨在找到兩個低維矩陣X(m×k)和矩陣Y(n×k)，來近似逼近R(m×n)，即：

其中R(m×n)代表用戶對商品的評分矩陣，X(m×k)代表用戶對隱含特征的偏好矩陣，Y(n×k)表示商品所包含隱含特征的矩陣，T表示矩陣Y的轉置。實際中，一般取k<<min(m, n), 也就是相當於降維了。這裏的低維矩陣，有的地方也叫低秩矩陣。

為了找到使低秩矩陣X和Y盡可能地逼近R，需要最小化下麵的平方誤差損失函數：

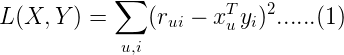其中x_u(1×k)表示示用戶u的偏好的隱含特征向量，y_i(1×k)表示商品i包含的隱含特征向量, r_ui表示用戶u對商品i的評分, 向量x^u和y_i的內積x_u^Ty_i是用戶u對商品i評分的近似。

損失函數一般需要加入正則化項來避免過擬合等問題，我們使用L2正則化，所以上麵的公式改造為：

其中λ是正則化項的係數。

到這裏，協同過濾就成功轉化成了一個優化問題。由於變量xu和yi耦合到一起，這個問題並不好求解，所以我們引入了ALS，也就是說我們可以先固定Y（例如隨機初始化X），然後利用公式（2）先求解X，然後固定X，再求解Y，如此交替往複直至收斂，即所謂的交替最小二乘法求解法。

具體求解方法說明如下：

• 先固定Y,  將損失函數L(X,Y)對x_u求偏導，並令導數=0，得到：

• 同理固定X，可得：

其中ru(1×n)是R的第u行,ri(1×m)是R的第i列， I是k×k的單位矩陣。

• 迭代步驟：首先隨機初始化Y，利用公式(3)更新得到X,  然後利用公式(4)更新Y,  直到均方根誤差變RMSE化很小或者到達最大迭代次數。

ALS-WR

上文提到的模型適用於解決有明確評分矩陣的應用場景，然而很多情況下，用戶沒有明確反饋對商品的偏好，也就是沒有直接打分，我們隻能通過用戶的某些行為來推斷他對商品的偏好。比如，在電視節目推薦的問題中，對電視節目收看的次數或者時長，這時我們可以推測次數越多，看得時間越長，用戶的偏好程度越高，但是對於沒有收看的節目，可能是由於用戶不知道有該節目，或者沒有途徑獲取該節目，我們不能確定的推測用戶不喜歡該節目。ALS-WR通過置信度權重來解決這些問題：對於更確信用戶偏好的項賦以較大的權重，對於沒有反饋的項，賦以較小的權重。ALS-WR模型的形式化說明如下：

• ALS-WR的目標函數：

其中α是置信度係數。

• 求解方式還是最小二乘法：

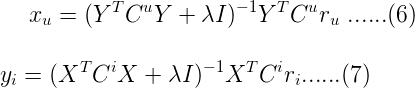其中C^u是n×n的對角矩陣，Ci是m×m的對角矩陣；C^u_ii  = c_ui,  Cⁱ_ii  = c_ii。

具體實現待補充。

本文參考：

[1] https://github.com/ceys/jdml/wiki/ALS

[2] http://mt.sohu.com/20150507/n412633357.shtml