KMP算法是一種線性時間複雜的字符串匹配算法,它是對BF算法(Brute-Force,最基本的字符串匹配算法的)改進。
對於給的的原始串S和模式串P,需要從字符串S中找到字符串P出現的位置的索引。
BF算法的時間複雜度O(strlen(S) * strlen(T)),空間複雜度O(1)。
KMP算法的時間複雜度O(strlen(S) + strlen(T)),空間複雜度O(strlen(T))。
假設現在S串匹配到i位置,T串匹配到j位置。那麽總的來說,兩種算法的主要區別在於失配的情況下,
對j的值做的處理:【注意,本文中的字符串下標都是從0開始計算】
BF算法中,如果當前字符匹配成功,即 s[i+j] == T[j],令 j++,繼續匹配下一個字符;如果失配,即 S[i + j] != T[j],
需要讓i++,並且j = 0, 即每次匹配失敗的情況下,模式串T相對於原始串S向右移動了一位 。 (請結合下文源代碼看這裏的分析)
而KMP算法中,如果當前字符匹配成功,即S[i]==T[j],令i++,j++,繼續匹配下一個字符;如果如果失配,即S[i] != T[j],
需要保持i不變,並且讓j = next[j],這裏next[j] <=j -1,即模式串T相對於原始串S向右移動了至少1位(移動的實際位數j – next[j] >=1 ),
同時移動之後,i之前的部分(即S[i-j+1 ~ i]和j=next[j]之前的部分(即T[0 ~ j-1])仍然相等。顯然,相對於BF算法來說,KMP移動更多的
位數,起到了一個加速的作用! ( 失配的特殊情形,令j=next[j]導致j==0的時候,需要將i ++,否則此時沒有移動模式串 )。(請結合下
文源代碼看這裏的分析)
下麵解釋一下next數組的含義,這個也是KMP算法中比較不好理解的一點。
令原始串為: S[i],其中0<=i<=n;模式串為: T[j],其中0<=j<=m。
假設目前匹配到如下位置
S0,S1,S2,…,Si-j,Si-j+1……………,Si-1, Si, Si+1,….,Sn
T0,T1,……………….,Tj-1, Tj, ……….
S和T的綠色部分匹配成功,恰好到Si和Tj的時候失配,如果要保持i不變,同時達到讓模式串T相對於原始串S右移的話,可以
更新j的值,讓S[i]和新的T[j]進行匹配,假設新的j用next[j]表示,即讓S[i]和T[next[j]]匹配,顯然新的j值要小於之前的j值,模式串才會是
右移的效果,也就是說應該有next[j] <= j -1。那新的j值也就是next[j]應該是多少呢?我們觀察如下的匹配:
1) 如果模式串右移1位,即next[j] = j – 1, 即讓S[i]和T[j-1]匹配 (注:省略號為未匹配部分)

根據【1】【2】可以知道當next[j] =j -1,即模式串右移一位的時候,有T[0 ~ j-2] == T[1 ~ j-1]。而這兩部分
恰好是字符串T[0 ~ j-1]的前綴和後綴,也就是說next[j]的值取決於模式串T中j前麵部分的前綴和後綴相等部分的長度。
2) 如果模式串右移2位,即next[j] = j – 2, 即讓S[i]和T[j-2]匹配

同樣根據【3】【4】可以知道當next[j] =j -2,即模式串右移兩位的時候,有T[0 ~ j-3] == T[2 ~ j-1]。而這兩部分
也敲好是字符串T[0 ~ j-1]的前綴和後綴,也就是說next[j]的值取決於模式串T中j前麵部分的前綴和後綴相等部分的長度
3) 依次類推,可以得到如下結論當發生失配的情況下,j的新值next[j]取決於模式串中T[0 ~ j-1]中前綴和後綴相等部分的長度,
並且next[j]恰好等於這個最大長度。
上麵給出了next數組的含義,下麵給出求這個數組的具體算法。
1)顯然有next[0] = 0, next[1] = 0;
2)觀察【1】【2】可以看到如果T[j]==T[j -1]即T[j] == T[next[j]]的情況下,j+1前麵字符串的前綴和後綴的相等部分長度增加了1
所以有T[j]==T[next[j]]的時候,next[j+1] = next[j ] + 1;
同樣觀察【3】【4】也可以看到如果T[j]==T[j-2]亦即T[j]==T[next[j]的情況下,j+1前麵的字符串的前綴和後綴相等部分的長度增加了1,
所以也有T[j]==T[next[j]]的時候,next[j+1] = next[j] + 1;
綜合上麵的規律有當T[j] == T[next[j]]的情況下next[j+1]=next[j] + 1;
3) 當T[j] != T[next[j]]的情況next[j+1]又該等於多少呢?拿【1】【2】來說,如果此時T[j] != T[j-1],可以移動【2】對應的串,
直到【1】中的Tj等於下麵【2】中對應的字符,此時就找到了j+1的最大前後綴。注意,移動的時候同樣可以用到已經計算出
的next數組的值。
用偽代碼表示就是:
k = next[j];
while(T[k] != T[j]) k = next[k];//如果不等,移動模式串
if(T[k] == T[j]) next[j + 1] = k + 1;
else next[j+1] = k;
最後給出BF算法和KMP算法(有四個版本)的源碼如下。
BF:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
int indexofsubstr(const char* str, const char* p)
{
int lenstr = strlen(str);
int lenp = strlen(p);
int i, j;
for(i = 0; i < lenstr; ++i)
{
j = 0;
while( i + j < lenstr && j < lenp && str[i + j] == p[j]) j++;
if(j == lenp) return i;
}
return -1;
}
int main(int argc, char** argv)
{
const char* str = "abcdefghijklmmnx";
const char* p = "mmn";
printf("index:%d\n", indexofsubstr(str, p));
system("pause");
return 0;
}
KMP V1.0
/*
* Author:puresky
* Date: 2010/12/21
* Purpose: KMP 1.0, a linear algorithm for searching pattern string in a given string!
*/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
//print a integer array
void pnt(int a[], int n)
{
int i;
for(i = 0; i < n; ++i) printf("%d ", a[i]);
printf("\n");
}
//calculate the next array
void makenext(const char* ptrn, int *next)
{
int len = strlen(ptrn);
next[0] = 0;
next[1] = 0;
int i = 1;
while(i < len - 1)
{
int j = next[i];
while(j > 0 && ptrn[j] != ptrn[i]) j = next[j];
if(ptrn[j] == ptrn[i]) next[i + 1] = j + 1;
else next[i + 1] = j;
i++;
}
//pnt(next, len);
}
//KMP
int indexofsubstr(const char* str, const char* ptrn)
{
int lenstr = strlen(str);
int lenptrn = strlen(ptrn);
int next[1024]; //假設模式串的長度不超過1024
makenext(ptrn, next);
int i = 0, j = 0;
while(i < lenstr && j < lenptrn)
{
if(str[i] == ptrn[j])
{
i++,j++;
}
else
{
j = next[j];
// if j euqals zero, increase i by 1. Otherwize, there may be a infinite loop!
if(j == 0) i++;
}
if(j == lenptrn) return i - j; //match successfully, return the index
}
return -1;
}
int main(int argc, char** argv)
{
const char* str = "abcdecdeabghijmnmnklamnmnaxabcabcabdxababacm";
const char* p[6] = {"abcabd", "mnmna","mmx", "aaaaaaaabac", "cdecdea", "ababacm"};
int i;
for(i = 0; i < 6; ++i)
{
printf("S:%s\n", str);
printf("P:%s\n", p[i]);
printf("Index:%d\n", indexofsubstr(str, p[i]));
printf("*******************************\n");
}
system("pause");
return 0;
}
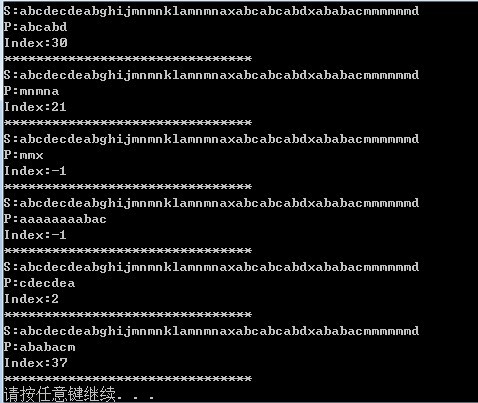
運行結果如下:
KMP V2.0
//在KMP 1.0的基礎上將next代碼簡化了一下,其思想為當模式串和模式串失配時,利用已經求出的next值將其中一個模式串
//移動適當的距離
#include <stdio.h>
#include <time.h>
#include <string.h>
#include <stdlib.h>
#define MAX_PATTERN_LEN 1024
void print(int *a, int n)
{
printf("next:");
int i;
for(i = 0; i < n; ++i) printf("%d ", a[i]);
printf("\n");
}
void randstr(char a[], int n)
{
int i;
for(i = 0; i < n; i++)
a[i] = 'a' + rand() % 3;
a[n - 1] = '\0';
}
void getnext(const char* t, int *next)
{
int len = strlen(t);
int i,j;
next[0] = 0;
next[1] = 0;
i = 1;
j = 0;
while(i < len)
{
if(t[i] == t[j])
{
i++,j++;
next[i] = j;
}
else
{
if(j == 0)
{
i++;
next[i] = 0;
}
j = next[j];
}
}
print(next, len);
}
// ensure strlen(t) < MAX_PATTERN_LEN
int KMP_Index(const char* s, const char* t)
{
int next[MAX_PATTERN_LEN];
getnext(t, next);
int lens = strlen(s);
int lent = strlen(t);
int i,j;
i = 0;
j = 0;
while(i < lens && j < lent)
{
if(s[i] == t[j])
{
i++, j++;
}
else
{
if(j == 0) i++;
j = next[j];
}
if(j == lent) return i - j;
}
return -1;
}
int main(int argc, char** argv)
{
srand(time(NULL));
int times = 20;
while(--times)
{
char s[1024];
char t[1024];
randstr(s, 100);
randstr(t, 5);
printf("S:%s\nT:%s\n", s, t);
int r1 = KMP_Index(s, t);
char* r2 = strstr(s, t);
printf("%d:%s\n", r1, r2);
if(r1 == -1 && r2 == NULL || r1 == r2 - s) printf("check:TRUE ^_^\n");
else printf("check:FALSE XXXX\n");
printf("----------------------------------------------------\n");
}
system("pause");
return 0;
}
KMP3.0
//KMP 2.0中,如果模式串為aaaaaaaa這種情形時,將會退化為BF算法,所以這裏對next的計算做了小小的改進
#include <stdio.h>
#include <time.h>
#include <string.h>
#include <stdlib.h>
#define MAX_PATTERN_LEN 1024
void print(int *a, int n)
{
printf("next:");
int i;
for(i = 0; i < n; ++i) printf("%d ", a[i]);
printf("\n");
}
void randstr(char a[], int n)
{
int i;
for(i = 0; i < n; i++)
a[i] = 'a' + rand() % 3;
a[n - 1] = '\0';
}
void getnext(const char* t, int *next)
{
int len = strlen(t);
int i,j;
next[0] = 0;
next[1] = 0;
i = 1;
j = 0;
while(i < len)
{
if(t[i] == t[j])
{
i++,j++;
//以下是改進的地方
if(t[i] == t[j])
next[i] = next[j];
else
next[i] = j;
}
else
{
if(j == 0)
{
i++;
next[i] = 0;
}
j = next[j];
}
}
print(next, len);
}
int KMP_Index(const char* s, const char* t)
{
int next[MAX_PATTERN_LEN];
getnext(t, next);
int lens = strlen(s);
int lent = strlen(t);
int i,j;
i = 0;
j = 0;
while(i < lens && j < lent)
{
if(s[i] == t[j])
{
i++, j++;
}
else
{
if(j == 0) i++;
j = next[j];
}
if(j == lent) return i - j;
}
return -1;
}
int main(int argc, char** argv)
{
srand(time(NULL));
int times = 20;
while(--times)
{
char s[1024];
char t[1024];
randstr(s, 100);
randstr(t, 5);
printf("S:%s\nT:%s\n", s, t);
int r1 = KMP_Index(s, t);
char* r2 = strstr(s, t);
printf("%d:%s\n", r1, r2);
if(r1 == -1 && r2 == NULL || r1 == r2 - s) printf("check:TRUE ^_^\n");
else printf("check:FALSE XXX\n");
printf("----------------------------------------------------\n");
}
system("pause");
return 0;
}
KMP4.0
//KMP算法的一種經典實現方法!
/*
* Author:puresky
* Date: 2010/12/22
* Version: KMP 4.0,
* Refer to:Handbook of Exact String-Matching Algorithms, Christian Charras & Thierry Lecroq
*/
#include <stdio.h>
#include <time.h>
#include <string.h>
#include <stdlib.h>
#define MAX_PATTERN_LEN 1024
//print the array
void print(int *a, int n)
{
printf("next:");
int i;
for(i = 0; i < n; ++i) printf("%d ", a[i]);
printf("\n");
}
//generate a random string
void randstr(char a[], int n)
{
int i;
for(i = 0; i < n; i++)
a[i] = 'a' + rand() % 3;
a[n - 1] = '\0';
}
//preprocessing for KMP
void preKMP(const char* t, int next[], int len)
{
int i,j;
next[0] = -1; //Attention: next[0] equals -1 other than 0
i = 0;
j = -1;
while(i < len)
{
while(j > -1 && t[j] != t[i])
j = next[j];
i++, j++;
if(t[j] == t[i])
next[i] = next[j];
else
next[i] = j;
}
print(next, len);//output the 'next' array
}
// KMP, ensure strlen(t) < MAX_PATTERN_LEN
int KMP(const char* s, const char* t)
{
int next[MAX_PATTERN_LEN];
int lens = strlen(s);
int lent = strlen(t);
preKMP(t, next, lent);
int i,j;
i = j = 0;
while(i < lens)
{
while(j > -1 && t[j] != s[i])
j = next[j];
i++, j++;
if(j >= lent) return i - j;
}
return -1;
}
int main(int argc, char** argv)
{
srand(time(NULL));
int times = 20;
while(--times)
{
char s[1024];
char t[1024];
randstr(s, 100);
randstr(t, 5);
printf("S:%s\nT:%s\n", s, t);
int r1 = KMP(s, t);
char* r2 = strstr(s, t);
printf("%d:%s\n", r1, r2);
if(r1 == -1 && r2 == NULL || r1 == r2 - s) printf("check:TRUE ^_^\n");
else printf("check:FALSE XXX\n");
printf("----------------------------------------------------\n");
}
system("pause");
return 0;
}