時間是每個涉及時間序列的機器學習問題中的黃金信息。作為數據科學家，我們必須盡最大努力提取時間模式。對於時間的預處理，常用的方法有：示例標準化(平穩性檢查，自相關刪除…)，創建和編碼類別時間特征(天，周，月，季節…)，手動特征工程(傅立葉變換…)等。這些方法並非總是有效，因為在建模期間，我們選擇的模型可能無法將時間本身正確地視為一項特征。

在這篇文章中，我嘗試重現論文“Time2Vec：學習時間的向量表示’（‘Time2Vec: Learning a Vector Representation of Time’），最終目的是為時間開發一個通用的表示形式，該表示形式可以在任何體係結構中潛在使用(我使用此解決方案在Keras中開發了神經網絡)。作者不想提出一個用於時間序列分析的新模型，而是以向量嵌入的形式提供時間表示，以便自動進行特征工程過程並以更好的方式對時間建模。

數據集

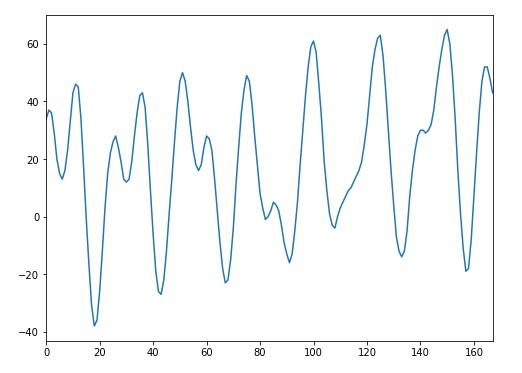
為了驗證整個解決方案的實用性，我們需要一個足夠的數據集。這裏我們需要純粹的時間序列格式的數據，不需要任何冗餘信息。這種情況在自回歸問題中很常見，在該問題中，我們隻有一個時間序列特征，我們將其用作預測未來的特征。在現實生活中，這是一項常見的任務，因此查找數據集並不困難。我們在Kaggle上發現了一個不錯的數據集，它存儲了威尼斯這個城市大量的曆史水位信息。預測這些值是一項艱巨的任務——在這裏，我們必須使用唯一的曆史時序水位數據以提供對下一小時水位的預測。

TIME2VEC的實現

從數學上講，實現Time2Vec非常容易：

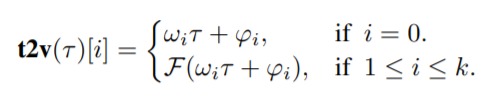
圖來源：https://arxiv.org/pdf/1907.05321.pdf

其中ķ是time2vec維度，τ是原始時間序列特征，F是周期性激活函數，ω和φ是一組可學習的參數。在實驗中，為了使得算法能夠捕獲數據中的周期性行為，F選定為一個正弦函數。與此同時線性項(對應i=0)表示時間的進程，可用於捕獲時間輸入中的非周期性模式。

簡單性使得該時間向量表示可以通過不同體係結構輕鬆使用。這裏，我嘗試通過簡單修改Keras Dense層以便在神經網絡結構中使用它。

class T2V(Layer):
    def __init__(self, output_dim=None, **kwargs):
        self.output_dim = output_dim
        super(T2V, self).__init__(**kwargs)
    def build(self, input_shape):
        
        self.W = self.add_weight(name='W', 
                      shape=(self.output_dim, 
                             self.output_dim),
                      initializer='uniform',
                      trainable=True)
        
        self.B = self.add_weight(name='B', 
                      shape=(input_shape[1], 
                             self.output_dim),
                      initializer='uniform',
                      trainable=True)
        
        self.w = self.add_weight(name='w', 
                      shape=(1, 1),
                      initializer='uniform',
                      trainable=True)
        
        self.b = self.add_weight(name='b', 
                      shape=(input_shape[1], 1),
                      initializer='uniform',
                      trainable=True)
        
        super(T2V, self).build(input_shape)
    def call(self, x):
        original = self.w * x + self.b
        x = K.repeat_elements(x, self.output_dim, -1)
        sin_trans = K.sin(K.dot(x, self.W) + self.B)
        return K.concatenate([sin_trans,original], -1)
    def compute_output_shape(self, input_shape):
        return (input_shape[0], input_shape[1], self.output_dim+1)

這個用戶自定義層的輸出維度是用戶指定的維度(1≤i≤k)，即從網絡學到的正弦波，加上輸入的線性表示(i = 0)。有了這個組件，我們隻需要將它與其他層堆疊在一起，然後在案例研究中嘗試使用它的強大功能。

模型

Time2Vec是否可以很好地表示時間？為了回答這個問題，我建立了兩種不同的序列神經網絡模型，比較了在預測任務中獲得的性能指標。第一個輸入是我們的自定義Time2Vec層作為輸入，該層堆疊在一個簡單的LSTM層上。第二層僅由先前結構中使用的簡單LSTM層組成。

def T2V_NN(dim, t2v_dim):
    inp = Input(shape=(dim,1))
    x = T2V(t2v_dim)(inp)
    x = LSTM(32)(x)
    x = Dense(1)(x)
    m = Model(inp, x)
    return m
def NN(dim):
    inp = Input(shape=(dim,1))
    x = LSTM(32)(inp)
    x = Dense(1)(x)
    m = Model(inp, x)
    return m

結果

我將數據的前70％用作訓練集，將其餘30％用作測試集。然後將模型訓練了100輪(epochs)，對於LSTM + T2V，MSE約為10.09，對於簡單LSTM，MSE約為13.12。

為了提供性能差異的證據，我決定比較最終預測的分布：

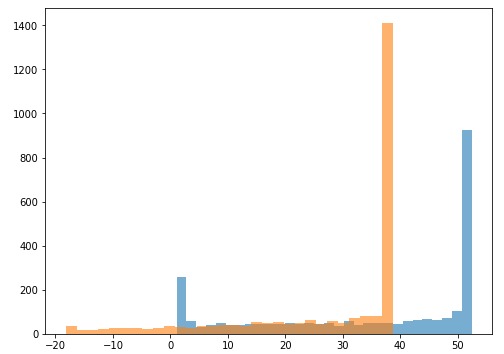
乍一看，分布之間有很多重疊。但是，我們無法看到兩個樣本之間在統計上是否存在顯著差異。在這種情況下自舉（bootstrapping ）方法可以幫助我們弄清楚這個差異！

自舉是一種隨機重采樣的直觀技術，它允許估計幾乎所有統計信息的采樣分布。它的實現非常容易。在我們的情況下，我們必須從預測分布中提取重複的小樣本，計算每個樣本的均值，創建這些均值的新分布，然後再做比較：

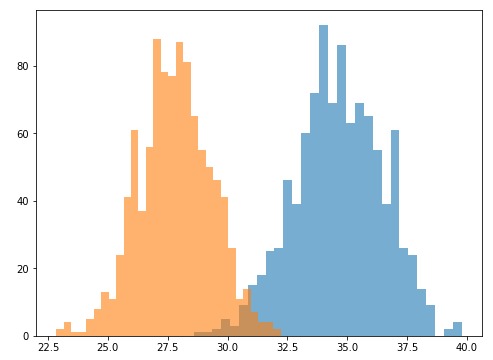
這兩個新的重采樣分布對我們來說很熟悉。它們是正太分布，因此比較起來更容易。為了方便比較，我將第一個分布的90分位數和第二個分布的10分位數進行比較，並檢查是否存在重疊。我們可以看到29.77(來自沒有T2V的LSTM)小於32.23(來自帶有T2V的LSTM)。換句話說，我們可以得出90％的置信度，即預測分布之間存在統計差異，並且Time2Vec能夠顯著提高性能。

總結

在這篇文章中，我介紹了一種自動學習時間特征的方法。特別是我們重現了論文中的Time2Vec，一種時間的向量表示，並調整使其適用於神經網絡架構。並且，我們能夠在實際任務中展示這種時間表示的有效性。正如論文的作者所建議的，Time2Vec(T2V)並不是用於時間序列分析的新模型，而是一種簡單的向量表示形式，可以輕鬆地將其導入許多現有和未來的模型體係結構中並改善其性能。

參考資料

Time2Vec：Learning a Vector Representation of Time（學習時間的向量表示）。 Seyed Mehran Kazemi，Rishab Goel，Sepehr Eghbali，Janahan Ramanan，Jaspreet Sahota，Sanjay Thakur，Stella Wu，Cathal Smyth，Pascal Poupart，Marcus Brubaker

本文來源

Time2Vec for Time Series features encoding