借助inverse_laplace_transform()方法,我们可以计算F(s)的拉普拉斯变换的逆。
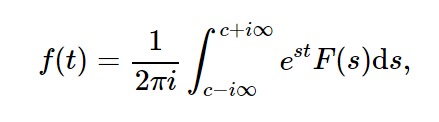
用法:inverse_laplace_transform(F, s, t)
返回:Return the unevaluated tranformation function.
范例1:
在这个例子中,我们可以通过使用inverse_laplace_transform()方法,我们能够计算拉普拉斯逆变换并返回未求值的函数。
# import inverse_laplace_transform
from sympy.integrals.transforms import inverse_laplace_transform
from sympy import exp, Symbol
from sympy.abc import s, t
a = Symbol('a', positive = True)
# Using inverse_laplace_transform() method
gfg = inverse_laplace_transform(exp(-a * s)/s, s, t)
print(gfg)输出:
Heaviside(-a + t)
范例2:
# import inverse_laplace_transform
from sympy.integrals.transforms import inverse_laplace_transform
from sympy import exp, Symbol
from sympy.abc import s, t
a = Symbol('a', positive = True)
# Using inverse_laplace_transform() method
gfg = inverse_laplace_transform(exp(-a * s)/s, s, 5)
print(gfg)输出:
Heaviside(5 - a)
相关用法
注:本文由纯净天空筛选整理自Jitender_1998大神的英文原创作品 sympy.integrals.inverse_laplace_transform() in python。非经特殊声明,原始代码版权归原作者所有,本译文未经允许或授权,请勿转载或复制。
