Python numpy random.mtrand.RandomState.noncentral_f用法及代码示例

用法：

RandomState.noncentral_f(dfnum, dfden, nonc, size=None)

从非中心F分布中抽取样本。

从具有指定参数dfnum(分子的自由度)和dfden(分母的自由度)的F分布中抽取样本，其中两个参数均大于1。nonc是非中心性参数。

参数：	dfnum： ： float 或 array_like of floats 分子自由度，必须> 0。 在版本1.14.0中更改：较早的NumPy版本要求dfnum> 1。 dfden： ： float 或 array_like of floats 分母的自由度必须大于0。 nonc： ： float 或 array_like of floats 非中心参数(分子平均值的平方和)必须> = 0。 size： ： int 或 tuple of ints, 可选参数 输出形状。如果给定的形状是(m, n, k)， 然后m * n * k抽取样品。如果尺寸是None(默认)，如果返回一个值dfnum，dfden和nonc都是标量。除此以外，np.broadcast(dfnum, dfden, nonc).size抽取样品。
返回值：	out： ： ndarray或标量 从参数化非中心Fisher分布中抽取样本。

注意：

在计算实验的功效时(功效=当特定选择为真时拒绝零假设的概率)，非中心F统计量变得非常重要。当原假设为真时，F统计量遵循中心F分布。当原假设不成立时，则遵循非中心F统计量。

参考文献：

[1]	Eric W. Weisstein，“非中央F-Distribution。”来自MathWorld-A Wolfram Web资源。http://mathworld.wolfram.com/NoncentralF-Distribution.html

[2]	维基百科，“非中央F-distribution”，https://en.wikipedia.org/wiki/Noncentral_F-distribution

例子：

在一项研究中，要测试零假设的特定替代方法，需要使用非中心F分布。我们需要计算分布尾部中超过原假设的F分布值的面积。我们将绘制两个概率分布以进行比较。

>>> dfnum = 3 # between group deg of freedom
>>> dfden = 20 # within groups degrees of freedom
>>> nonc = 3.0
>>> nc_vals = np.random.noncentral_f(dfnum, dfden, nonc, 1000000)
>>> NF = np.histogram(nc_vals, bins=50, density=True)
>>> c_vals = np.random.f(dfnum, dfden, 1000000)
>>> F = np.histogram(c_vals, bins=50, density=True)
>>> import matplotlib.pyplot as plt
>>> plt.plot(F[1][1:], F[0])
>>> plt.plot(NF[1][1:], NF[0])
>>> plt.show()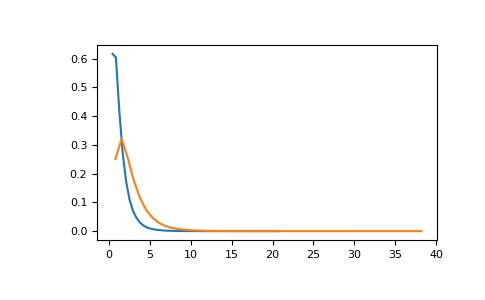

注：本文由纯净天空筛选整理自 numpy.random.mtrand.RandomState.noncentral_f。非经特殊声明，原始代码版权归原作者所有，本译文未经允许或授权，请勿转载或复制。