Python numpy random.mtrand.RandomState.gumbel用法及代码示例

用法： RandomState.gumbel(loc=0.0, scale=1.0, size=None)

从Gumbel分布中抽取样本。

从具有指定位置和比例的Gumbel分布中抽取样本。有关Gumbel分布的更多信息，请参见下面的注释和参考。

参数：

参数：	loc：： float 或 array_like of floats, 可选参数分布方式的位置。默认值为0。 scale：： float 或 array_like of floats, 可选参数分布的比例参数。默认值为1。必须为非负数。 size：： int 或 tuple of ints, 可选参数输出形状。如果给定的形状是`(m, n, k)`，然后`m * n * k`抽取样品。如果尺寸是`None`(默认)，如果返回一个值`loc`和`scale`都是标量。除此以外，`np.broadcast(loc, scale).size`抽取样品。
返回值：	out：： ndarray或标量从参数化的Gumbel分布中抽取样本。

loc：： float 或 array_like of floats, 可选参数: 分布方式的位置。默认值为0。
scale：： float 或 array_like of floats, 可选参数: 分布的比例参数。默认值为1。必须为非负数。
size：： int 或 tuple of ints, 可选参数: 输出形状。如果给定的形状是(m, n, k)，然后m * n * k抽取样品。如果尺寸是None(默认)，如果返回一个值loc和scale都是标量。除此以外，np.broadcast(loc, scale).size抽取样品。

返回值：

out：： ndarray或标量: 从参数化的Gumbel分布中抽取样本。

注意：

Gumbel(或最小极值(SEV)或I最小极值类型)分布是用于建模极值问题的一类广义极值(GEV)分布之一。 Gumbel是I极值类型分布的一种特例，用于从具有“exponential-like”尾部的分布中获得最大值。

Gumbel分布的概率密度为

$p(x) = \frac{e^{-(x - \mu)/ \beta}}{\beta} e^{ -e^{-(x - \mu)/ \beta}},$

哪里 $\mu$ 是模式，位置参数，以及 $\beta$ 是scale参数。

Gumbel(以德国数学家Emil Julius Gumbel的名字命名)在水文学中很早就被用来模拟洪水事件的发生。它也用于建模最大风速和降雨量。它是“fat-tailed”分布-分布尾部发生事件的概率大于使用高斯分布的事件，因此令人惊讶地频繁发生了100年的洪水。洪水最初被建模为高斯过程，这高估了极端事件的发生频率。

它是一类极值分布，即通用极值(GEV)分布，其中还包括Weibull和Frechet。

该函数的平均值为 $\mu + 0.57721\beta$ 和方差 $\frac{\pi^2}{6}\beta^2$ 。

参考文献：

[1]	E. J. Gumbel，“极端情况的统计”，纽约：哥伦比亚大学出版社，1958年。

[2]	Reiss，R.-D.和Thomas M.，“来自保险，金融，水文学和其他领域的极值统计分析”，巴塞尔：Birkhauser Verlag，2001年。

例子：

从分布中抽取样本：

>>> mu, beta = 0, 0.1 # location and scale
>>> s = np.random.gumbel(mu, beta, 1000)

显示样本的直方图以及概率密度函数：

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 30, density=True)
>>> plt.plot(bins, (1/beta)*np.exp(-(bins - mu)/beta)
...          * np.exp( -np.exp( -(bins - mu) /beta) ),
...          linewidth=2, color='r')
>>> plt.show()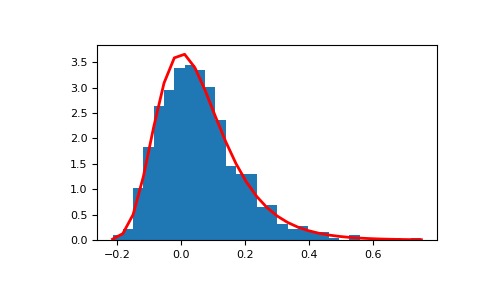

../../../_images/numpy-random-mtrand-RandomState-gumbel-1_00_00.png

说明高斯过程如何产生极值分布，并与高斯进行比较：

>>> means = []
>>> maxima = []
>>> for i in range(0,1000) :
...    a = np.random.normal(mu, beta, 1000)
...    means.append(a.mean())
...    maxima.append(a.max())
>>> count, bins, ignored = plt.hist(maxima, 30, density=True)
>>> beta = np.std(maxima) * np.sqrt(6) / np.pi
>>> mu = np.mean(maxima) - 0.57721*beta
>>> plt.plot(bins, (1/beta)*np.exp(-(bins - mu)/beta)
...          * np.exp(-np.exp(-(bins - mu)/beta)),
...          linewidth=2, color='r')
>>> plt.plot(bins, 1/(beta * np.sqrt(2 * np.pi))
...          * np.exp(-(bins - mu)**2 / (2 * beta**2)),
...          linewidth=2, color='g')
>>> plt.show()

../../../_images/numpy-random-mtrand-RandomState-gumbel-1_01_00.png

注：本文由纯净天空筛选整理自 numpy.random.mtrand.RandomState.gumbel。非经特殊声明，原始代码版权归原作者所有，本译文未经允许或授权，请勿转载或复制。