在數學中,微分方程,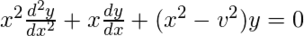 具有特別重要的意義。方程的解是參數的函數
具有特別重要的意義。方程的解是參數的函數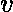 。對於積分和半積分值
。對於積分和半積分值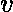 ,特別令人感興趣的解,被稱為圓柱貝塞爾函數,以著名的德國數學家弗裏 Delhi 希·威廉·貝塞爾的名字命名。要求的原因
,特別令人感興趣的解,被稱為圓柱貝塞爾函數,以著名的德國數學家弗裏 Delhi 希·威廉·貝塞爾的名字命名。要求的原因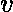 是積分還是半積分將在下麵給出的解釋中清楚。
由於這是一個二階微分方程,必然有兩個線性獨立的解,稱為第一類和第二類。因此,可以使用以下公式手動求解微分方程弗羅貝尼烏斯法。用於複雜參數的第一類貝塞爾函數
是積分還是半積分將在下麵給出的解釋中清楚。
由於這是一個二階微分方程,必然有兩個線性獨立的解,稱為第一類和第二類。因此,可以使用以下公式手動求解微分方程弗羅貝尼烏斯法。用於複雜參數的第一類貝塞爾函數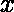 ,被稱為第一類修正貝塞爾函數,並表示為
,被稱為第一類修正貝塞爾函數,並表示為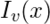 。該方法的應用產生了一個無限級數,其中包含以下項:
。該方法的應用產生了一個無限級數,其中包含以下項: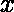 和
和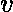 , 給出,
, 給出,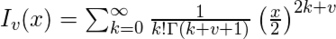 由於表達式中包含 Gamma Function,隻能計算積分和半積分值,因此參數
由於表達式中包含 Gamma Function,隻能計算積分和半積分值,因此參數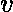 必須是積分或半積分。
C++17 (GCC 7.1) 標準庫
輸出:
必須是積分或半積分。
C++17 (GCC 7.1) 標準庫
輸出:
cmath給出計算第一類圓柱貝塞爾函數值的函數(std::cyl_bessel_j)(這裏沒有討論,但與我們討論的非常相似)和正則修正貝塞爾函數的值(std::cyl_bessel_i)。兩者對於小輸入都具有相當高的精度,並且可用於各種工程應用。例子:
Input: x = 2.798465, v = 0 Output: 4.152234090041574 Input: x = 3.04513, v = 0.5 Output: 4.792979684692604注意:以下源代碼隻能在 C++17 及更高版本上運行。可以檢查給定代碼的運行示例這裏。要運行不同的輸入,請訪問鏈接並單擊右下角的“Edit”。
// C++17 code for bessel function
#include <bits/stdc++.h>
using namespace std;
// Compute the answer from the formulae for first 10 terms
long double answer(long double x, long double v)
{
long double ans_by_expansion = 0;
long double fact = 1;
for (int k = 0; k < 10; fact = fact * (++k)) {
ans_by_expansion += pow((x / 2), (2 * k)) / pow(fact, 2);
cout << "ans_by_expansion till term k = ";
cout << k << " is " << ans_by_expansion << "\n";
}
return ans_by_expansion;
}
// Driver code
int main()
{
long double x = 2.798465;
long double v = 0;
// Compute the Regular Modified Bessel Function
// for v = 0, x = 2.798465
long double ans_by_function = cyl_bessel_i(v, x);
cout << setprecision(15) << fixed;
cout << "The answer by function for "
<< "Regular_Modified_Bessel_Function" << endl
<< "(" << v << ", " << x << ") = "
<< ans_by_function << "\n";
// calculate answer by expansion
long double ans_by_expansion = answer(x, v);
cout << "Absolute Error in answer by both the methods is = ";
cout << abs(ans_by_expansion - ans_by_function) << "\n";
return 0;
} The answer by function for Regular_Modified_Bessel_Function (0.000000000000000, 2.798465000000000) = 4.152234090041574 ans_by_expansion till term k = 0 is 1.000000000000000 ans_by_expansion till term k = 1 is 2.957851589056250 ans_by_expansion till term k = 2 is 3.916147300248771 ans_by_expansion till term k = 3 is 4.124614053687001 ans_by_expansion till term k = 4 is 4.150123238967278 ans_by_expansion till term k = 5 is 4.152120966924739 ans_by_expansion till term k = 6 is 4.152229612892962 ans_by_expansion till term k = 7 is 4.152233953968095 ans_by_expansion till term k = 8 is 4.152234086767796 ans_by_expansion till term k = 9 is 4.152234089977698 Absolute Error in answer by both the methods is = 0.000000000063876
相關用法
- C++17 std::clamp用法及代碼示例
- C++17 std::lcm用法及代碼示例
- C++17 std::variant用法及代碼示例
- C++11 std::initializer_list用法及代碼示例
- C++11 std::move_iterator用法及代碼示例
- C++14 std::integer_sequence用法及代碼示例
- C++14 std::quoted用法及代碼示例
- C++14 std::make_unique用法及代碼示例
- C++ cos()用法及代碼示例
- C++ sin()用法及代碼示例
- C++ asin()用法及代碼示例
- C++ atan()用法及代碼示例
- C++ atan2()用法及代碼示例
- C++ acos()用法及代碼示例
- C++ tan()用法及代碼示例
- C++ sinh()用法及代碼示例
- C++ ceil()用法及代碼示例
- C++ tanh()用法及代碼示例
- C++ fmod()用法及代碼示例
- C++ acosh()用法及代碼示例
- C++ asinh()用法及代碼示例
- C++ floor()用法及代碼示例
- C++ atanh()用法及代碼示例
- C++ log()用法及代碼示例
- C++ trunc()用法及代碼示例
注:本文由純淨天空篩選整理自AayushChaturvedi大神的英文原創作品 std::cyl_bessel_i in C++17。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
