Python numpy random.mtrand.RandomState.lognormal用法及代碼示例

用法： RandomState.lognormal(mean=0.0, sigma=1.0, size=None)

從log-normal分布中抽取樣本。

從具有指定平均值，標準偏差和數組形狀的log-normal分布中抽取樣本。請注意，均值和標準差不是分布本身的值，而是其基礎正態分布的值。

參數：

參數：	mean：： float 或 array_like of floats, 可選參數基本正態分布的平均值。默認值為0。 sigma：： float 或 array_like of floats, 可選參數基本正態分布的標準偏差。必須為非負數。默認值為1。 size：： int 或 tuple of ints, 可選參數輸出形狀。如果給定的形狀是`(m, n, k)`，然後`m * n * k`抽取樣品。如果尺寸是`None`(默認)，如果返回一個值`mean`和`sigma`都是標量。除此以外，`np.broadcast(mean, sigma).size`抽取樣品。
返回值：	out：： ndarray或標量從參數化的log-normal分布中抽取樣本。

mean：： float 或 array_like of floats, 可選參數: 基本正態分布的平均值。默認值為0。
sigma：： float 或 array_like of floats, 可選參數: 基本正態分布的標準偏差。必須為非負數。默認值為1。
size：： int 或 tuple of ints, 可選參數: 輸出形狀。如果給定的形狀是(m, n, k)，然後m * n * k抽取樣品。如果尺寸是None(默認)，如果返回一個值mean和sigma都是標量。除此以外，np.broadcast(mean, sigma).size抽取樣品。

返回值：

out：： ndarray或標量: 從參數化的log-normal分布中抽取樣本。

注意：

如果log(x)正態分布，則變量x的分布為log-normal。 log-normal分布的概率密度函數為：

$p(x) = \frac{1}{\sigma x \sqrt{2\pi}} e^{(-\frac{(ln(x)-\mu)^2}{2\sigma^2})}$

哪裏 $\mu$ 是卑鄙的 $\sigma$ 是變量的正態分布對數的標準偏差。如果隨機變量是大量獨立identically-distributed變量的乘積，則會產生log-normal分布，其方式與如果變量是大量獨立identically-distributed變量的總和會產生正態分布的方式相同。

參考文獻：

[1]	Limpert，E.，Stahel，W. A.和Abbt，M.，“跨科學的Log-normal分布：鍵和線索”，《生物科學》，第1卷。 51，第5號，2001年5月。https://stat.ethz.ch/~stahel/lognormal/bioscience.pdf

[2]	Reiss，R.D。和Thomas，M。，“極值的統計分析”，巴塞爾：Birkhauser Verlag，2001年，第31-32頁。

例子：

從分布中抽取樣本：

>>> mu, sigma = 3., 1. # mean and standard deviation
>>> s = np.random.lognormal(mu, sigma, 1000)

顯示樣本的直方圖以及概率密度函數：

>>> import matplotlib.pyplot as plt
>>> count, bins, ignored = plt.hist(s, 100, density=True, align='mid')

>>> x = np.linspace(min(bins), max(bins), 10000)
>>> pdf = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))
...        / (x * sigma * np.sqrt(2 * np.pi)))

>>> plt.plot(x, pdf, linewidth=2, color='r')
>>> plt.axis('tight')
>>> plt.show()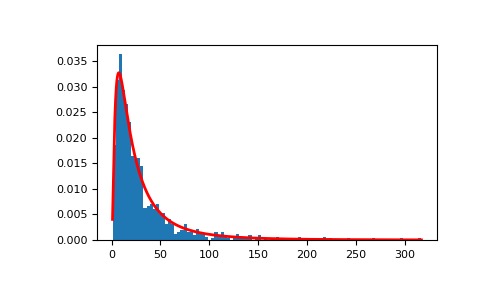

../../../_images/numpy-random-mtrand-RandomState-lognormal-1_00_00.png

證明通過log-normal概率密度函數可以很好地擬合均勻分布的隨機樣本的乘積。

>>> # Generate a thousand samples:each is the product of 100 random
>>> # values, drawn from a normal distribution.
>>> b = []
>>> for i in range(1000):
...    a = 10. + np.random.standard_normal(100)
...    b.append(np.product(a))

>>> b = np.array(b) / np.min(b) # scale values to be positive
>>> count, bins, ignored = plt.hist(b, 100, density=True, align='mid')
>>> sigma = np.std(np.log(b))
>>> mu = np.mean(np.log(b))

>>> x = np.linspace(min(bins), max(bins), 10000)
>>> pdf = (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2))
...        / (x * sigma * np.sqrt(2 * np.pi)))

>>> plt.plot(x, pdf, color='r', linewidth=2)
>>> plt.show()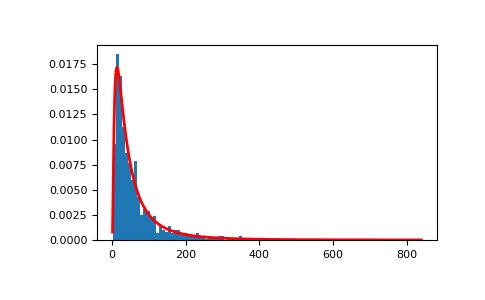

../../../_images/numpy-random-mtrand-RandomState-lognormal-1_01_00.png

相關用法

python scipy stats.lognorm用法及代碼示例

注：本文由純淨天空篩選整理自 numpy.random.mtrand.RandomState.lognormal。非經特殊聲明，原始代碼版權歸原作者所有，本譯文未經允許或授權，請勿轉載或複製。