當前位置: 首頁>>數據結構>>正文

KD樹/K-D樹

@ ▣數據結構, 算法&結構 ♢

本文理解翻譯自：http://en.wikipedia.org/wiki/K-d_tree

k-d樹(k-d tree)

來自維基百科，自由的百科全書

簡介

k-d樹是二叉樹的一種，樹中每個節點都是一個多維(k-dimension)的數據點。每個非葉子節點都可以看做是隱含的分割超平麵，該平麵將空間分成兩部分（也叫半空間）。超平麵左邊的點由k-d樹的左子樹表示，右邊的點由右子樹表示。選擇超平麵的方式為：樹中的每個節點對應K個維度中的一維，超平麵會垂直這個維度的坐標軸。例如，如果選擇X軸做分割，那麽所有X值小當前樹節點的點都在當前樹節點的左子樹中，所有X值大於當前樹節點的點都在當前樹節點的右子樹中。在這種情況下，超平麵是通過點的x值來設置，它的法向量(normal)就是單位X軸。[1]

k-d樹的操作

建樹

有很多方法可以用來選擇坐標軸分割平麵，所以有許多不同的構建k-d樹方法。比較權威的k-d建樹方法有下麵幾個約束：[2]

  • 在建樹過程中，循環使用每個坐標來選擇分割平麵。（例如，在一個3D樹中，根節點使用x對應的平麵，根節點的兒子選擇y對應的平麵，根節點的孫子選擇z對應的平麵，曾孫使用x對應的平麵，玄孫使用y對應的平麵，如此往複。）
  • 選擇了分割麵之後，將所有點對應維度的中值（中位數）所在點作為當前的樹節點。

這種方法可以創建一個平衡k-d樹，平衡的意思是說每個葉節點到根節點的距離大致相同。但是，平衡樹並不是對所有應用都是最優的。
另外要注意的是選擇中值也不是必須的。這種情況下，不保證樹的平衡。一個簡單的啟發方法用來避免編寫複雜的median-finding(O(N))算法[3][4] ，或者使用 Heapsort or Mergesort排序(O(nlogn)，具體做法是隨機挑選指定數量（小於n）的點取中值用於分割平麵。實踐中，這個技術通常能夠產生很平衡的k-d樹。
給定一個長度為n的點鏈表，下麵的算法使用中值選擇排序來創建平衡k-d樹。

function kdtree (list of points pointList, int depth)
{
    // Select axis based on depth so that axis cycles through all valid values
    var int axis := depth mod k;
        
    // Sort point list and choose median as pivot element
    select median by axis from pointList;
        
    // Create node and construct subtrees
    var tree_node node;
    node.location := median;
    node.leftChild := kdtree(points in pointList before median, depth+1);
    node.rightChild := kdtree(points in pointList after median, depth+1);
    return node;
}

通常在中值“之後”的點應該隻包括嚴格大於中值的點。對於中值對應的點，it is possible to define a “superkey” function that compares the points in all dimensions。在某些情況下，等於中值的點放在某一邊也是可以的，例如，將點分成“小於“子集和“大於等於”子集。
上麵的算法用Python實現的例程如下：

from collections import namedtuple
from operator import itemgetter
from pprint import pformat

class Node(namedtuple('Node', 'location left_child right_child')):
    def __repr__(self):
        return pformat(tuple(self))

def kdtree(point_list, depth=0):
    try:
        k = len(point_list[0]) # assumes all points have the same dimension
    except IndexError as e: # if not point_list:
        return None
    # Select axis based on depth so that axis cycles through all valid values
    axis = depth % k
 
    # Sort point list and choose median as pivot element
    point_list.sort(key=itemgetter(axis))
    median = len(point_list) // 2 # choose median
 
    # Create node and construct subtrees
    return Node(
        location=point_list[median],
        left_child=kdtree(point_list[:median], depth + 1),
        right_child=kdtree(point_list[median + 1:], depth + 1)
    )

def main():
    """Example usage"""
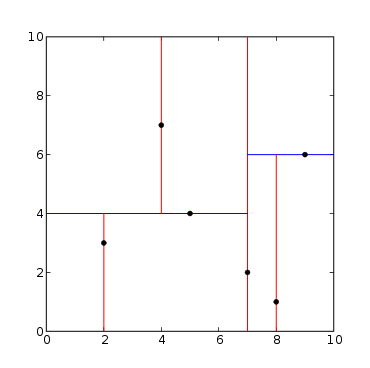
    point_list = [(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)]
    tree = kdtree(point_list)
    print(tree)

if __name__ == '__main__':
    main()
輸出如下：
((7, 2),
 ((5, 4), ((2, 3), None, None), ((4, 7), None, None)),
 ((9, 6), ((8, 1), None, None), None))

生成的樹如下圖所示：

370px-Kdtree_2d.svg

 

上麵的k-d樹分解了點集:(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)。

sss

上圖是k-d樹結果。

上麵的算法為每個節點做了一個不變的條件規定：所有左子樹的節點在分割麵的一邊，所有右子樹的節點在分割麵的另一邊。分類麵上的點可以在任意一邊。當前節點存儲分類麵上的值（代碼中是node.location)。
創建平衡k-d樹的另外一種算法是：建樹之前對數據預排序。然後在建樹的過程中維護這個順序，從而消除了每層分支時查找中值的開銷。在三維計算機器圖形中，有兩個這樣的算法通過構造平衡k-d樹來排序三角形，從而提升光纖追蹤的性能。這些算法在建樹之前預排序n個三角形，然後以O(n logn)的最好時間複雜度建樹；但是，這些算法的最壞時間複雜度很難預測，因為它依賴於計算機圖形中三角形的特定排列。[5][6] 與這些算法相比，有一個算法能夠通過排序點集以O(kn logn)的最壞時間複雜度排序建樹。這個算法首先使用Heapsort 或 Mergesort 以O(n logn)的時間複雜度在每個維度(共k個）上預排序n個點，然後在建樹過程中維護這k維的順序，因此能夠獲得最壞時間複雜度O(kn logn)。

添加元素

[icon] This section requires expansion.(November 2008)

向k-d樹添加節點跟其他搜索樹添加節點的方式一樣。首先，遍曆樹，從根節點開始，將待插入點跟當前節點比較確定是在那個分割麵，從而選擇繼續遍曆左兒子節點還是右兒子節點。一旦找到了可以添加到下麵的節點，將新的待插入點作為左兒子或者右兒子節點添加到樹中，“左”還是“右”取決於該節點跟分類麵的關係。
按這種方式添加節點可能會導致樹失去平衡，從而降低樹的性能。樹性能的降低比例取決於樹之前的空間分布，以及添加的節點數和樹原大小的關係。如果輸變得很不平衡，就需要做均衡了，從而恢複依賴於樹平衡的查詢性能，例如最近鄰居查詢。

刪除節點

[icon] This section requires expansion.(February 2011)

從已有k-d樹中刪除節點，且不破壞限製條件，最簡單的方法是將待刪除節點及其子樹做成集合，並重新建立子樹。
另外一個方法是為待刪除點找一個替代點。[8] 首先，找到包含待刪除點的節點R；如果R是葉子節點，不需要替換；如果是其他情況，從以R為根的子樹中找到一個替代點，設為p；交換R和p；然後，遞歸刪除p。
找到一個可替換點的方法： 假設節點R通過x軸來區分，並且R有一個右兒子，找到這個右兒子及其子樹中x值最小的點，即為可替換點。反之，找到右兒子及其子樹中x值最大的點，即為可替換點。

平衡

k-d樹的平衡需要非常小心，因為k-d樹通過多個維度來排序，所以tree rotation這樣的技術不能用來做平衡，原因是這個技術可能破壞k-d樹的限製條件。
Several variants of balanced k-d trees exist. They include divided k-d tree, pseudo k-d tree, k-d B-tree, hB-tree and Bkd-tree. Many of these variants are adaptive k-d trees.
k-d樹有幾種變體，包括：divided k-d tree、pseudo k-d tree、 k-d B-tree、Bkd-tree。這寫變體裏麵有許多是自適應k-d樹。

近鄰搜索

上圖是二維k-d樹中的NN搜索的動畫

近鄰搜索(NN)算法旨在從樹中找到離給定的點最近的點。這個檢索可以通過k-d樹的特性快速縮減大部分搜索空間而高效實現。
從k-d樹中查找最近鄰點按下列步驟進行：

  1. 從跟節點開始，遞歸向下遍曆，這個添加節點是一樣的（例如：向左還是向右取決於待查點在分割維度上比當前點小還是大）。
  2. 一旦找到葉子節點，就將該節點保存為“當前最佳”。
  3. 回溯，對每個節點執行下列步驟：
    1. 如果當前節點比“當前最佳”更接近待查節點，更新該節點為“當前最佳”
    2. 檢查在分割麵的另一邊是否有比“當前最佳”離待查點更近的節點。從概念上來說，以待查點為中心、以當前最近距離為半徑畫一個超球麵，看這個超球麵是否穿過了分割平麵。因為平麵都是坐標軸對應的，所以隻需要簡單比較待查點和當前點的在分裂麵上的那個維度的差值是否比當前最佳距離小。
      1. 如果超球麵穿越的分割麵，那麽分割麵的另外一側可能有最近點，所以需要遞歸遍曆樹的另外的分支，從而尋找更近的點。
      2. 如果超球麵沒有穿過分割麵，繼續遍曆其他節點，但是分割麵另外一邊的整個分支會被剪掉。
  4. 當算法最後回溯到根節點的時候，檢索完成。

通常，算法使用平方距離來做比較，而不是計算（更耗時的）平方根。另外，可以通過維持當前最好的平方距離來節省計算量。
在隨機分布的數據點上，查找最近點是一個O(log n)操作，這個分析比較麻煩。但是有算法聲明可以保證O(log n)的時間複雜度。[9] 在高維度空間，維數災難會導致算法需要訪問遠多於低維空間的分支。在實踐中，如果點數比維數大不了多少，算法隻能略好於線性遍曆所有的點。
這個算法也可以通過簡單地修改做多種擴展。比如，可用於計算k個最近鄰點，這個時候需要保存k個當前最佳而不是一個。分支能夠剪掉的條件是：k個點都找到，並且分支中沒有比這k個最佳更近的點。
還可以做近似是算法更快。例如：近似最近點查找可以通過指定檢查點的上限來實現，也可以基於實時時鍾（硬件實現更合適）終止檢索過程。【如果是查找已經在樹中的最近鄰點，隻需要看節點的距離是否為0就可以了，這有個缺點就是可能會丟棄重複、但是和待查點一致的節點。Nearest neighbour for points that are in the tree already can be achieved by not updating the refinement for nodes that give zero distance as the result, this has the downside of discarding points that are not unique, but are co-located with the original search point.（這一句理解不夠，把原文放這了）】
近似的近鄰查找在實時程序中比較有價值，例如機器人的顯著性能提升就是通過非窮舉搜索來獲得的。一種實現是：best-bin-first search。

範圍搜索

範圍搜索指的是使用範圍參數來做檢索。例如，如果一個k-d樹存儲的是收入和年齡的數值，那麽一個範圍搜索可能是：查找樹中年齡在20到50，收入在50000到80000的節點。應為k-d樹在樹的每一層對域的範圍做了分割，所以可以高效執行範圍查詢。
Analyses of binary search trees has found that the worst case time for range search in a k-dimensional KD tree containing N nodes is given by the following equation.[10] 二叉搜索樹的分析表明：在包含N個節點的k-d樹中做範圍查找，最壞時間複雜度如下：

c87a8a402c54f38a144411d38e6ebe10

高維數據

k-d trees are not suitable for efficiently finding the nearest neighbour in high-dimensional spaces. As a general rule, if the dimensionality is k, the number of points in the data, N, should be N >> 2k. Otherwise, when k-d trees are used with high-dimensional data, most of the points in the tree will be evaluated and the efficiency is no better than exhaustive search,[11] and approximate nearest-neighbour methods should be used instead.
在高維空間，k-d樹是不適合做高效的近鄰查詢。通常原則是，如果維度是k, 數據點數是N， 需要滿足N >> 2k。否則，當k-d樹用在高維度數據上，查找時絕大多數節點需要做評估，所以性能不一定比窮舉搜索好[11]，應該替換為一個近似的近鄰查詢。

複雜度

  • 從n個節點創建一個靜態的k-d樹有下列最壞時間複雜度：
    • O(n log2 n)  在建樹過程中，每層使用像Heapsort 或 Mergesort 這樣的O(n logn)算法查找中值。
    • O(n log n) 使用線性查找均值算法median of medians [3][4] 。
    • O(kn log n) 對n個節點每一維做了與排序，使用Heapsort or Mergesort這樣的時間複雜度為O(nlogn)的排序方法。 [7]
  • 插入一個新節點到平衡k-d樹, 時間複雜度為O(log n)
  • 從平衡k-d樹中刪除一個節點, 時間複雜度為O(log n)
  • 在平衡k-d樹中，做坐標軸平行的範圍查詢的時間複雜度是O(n1-1/k +m)，其中m是要返回的節點數，k是k-d樹的維度。
  • 在用隨機分布的數據構造的平衡二叉樹上，查找一個最近鄰的平均時間複雜度是：O(log n) 。

翻譯待續…..

Variations

Volumetric objects

Instead of points, a k-d tree can also contain rectangles or hyperrectangles.[12][13] Thus range search becomes the problem of returning all rectangles intersecting the search rectangle. The tree is constructed the usual way with all the rectangles at the leaves. In an orthogonal range search, the opposite coordinate is used when comparing against the median. For example, if the current level is split along xhigh, we check the xlow coordinate of the search rectangle. If the median is less than the xlow coordinate of the search rectangle, then no rectangle in the left branch can ever intersect with the search rectangle and so can be pruned. Otherwise both branches should be traversed. See also interval tree, which is a 1-dimensional special case.

Points only in leaves

It is also possible to define a k-d tree with points stored solely in leaves.[2] This form of k-d tree allows a variety of split mechanics other than the standard median split. The midpoint splitting rule[14] selects on the middle of the longest axis of the space being searched, regardless of the distribution of points. This guarantees that the aspect ratio will be at most 2:1, but the depth is dependent on the distribution of points. A variation, called sliding-midpoint, only splits on the middle if there are points on both sides of the split. Otherwise, it splits on point nearest to the middle. Maneewongvatana and Mount show that this offers “good enough” performance on common data sets. Using sliding-midpoint, an approximate nearest neighbour query can be answered in 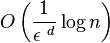O \left ( \frac{ 1 }{ { \epsilon\ }^d } \log n \right ). Approximate range counting can be answered in O \left ( \log n + { \left ( \frac{1}{ \epsilon\ } \right ) }^d \right ) with this method.

See also

  • implicit k-d tree, a k-d tree defined by an implicit splitting function rather than an explicitly-stored set of splits
  • min/max k-d tree, a k-d tree that associates a minimum and maximum value with each of its nodes
  • Ntropy, computer library for the rapid development of algorithms that uses a kd-tree for running on a parallel computer
  • Octree, a higher-dimensional generalization of a quadtree
  • Quadtree, a space-partitioning structure that splits at the geometric midpoint rather than the median coordinate
  • R-tree and bounding interval hierarchy, structure for partitioning objects rather than points, with overlapping regions
  • Recursive partitioning, a technique for constructing statistical decision trees that are similar to k-d trees
  • Klee’s measure problem, a problem of computing the area of a union of rectangles, solvable using k-d trees
  • Guillotine problem, a problem of finding a k-d tree whose cells are large enough to contain a given set of rectangles
  • Ball tree, a multi-dimensional space partitioning useful for nearest neighbor search

References

External links

本文由《純淨天空》出品。文章地址: https://vimsky.com/zh-tw/article/613.html，未經允許，請勿轉載。