我的數據集包含許多數字屬性和一個類別屬性。
比方說,NumericAttr1, NumericAttr2, ..., NumericAttrN, CategoricalAttr,
其中CategoricalAttr取三個可能值之一:CategoricalAttrValue1,CategoricalAttrValue2或CategoricalAttrValue3。
我正在使用Octave https://blog.west.uni-koblenz.de/2012-07-14/a-working-k-means-code-for-octave/的默認k-means聚類算法實現。但它僅適用於數值數據。
所以我的問題是:將分類屬性CategoricalAttr拆分為三個數字(二進製)變量(如IsCategoricalAttrValue1, IsCategoricalAttrValue2, IsCategoricalAttrValue3)是否正確?
最佳解決方法
由於各種原因,標準k-means算法不能直接應用於類別數據。類別數據的樣本空間是離散的,並且沒有自然來源。在這樣的空間上的歐幾裏德距離函數並不是真正有意義的。正如有人所說的那樣,“The fact a snake possesses neither wheels nor legs allows us to say nothing about the relative value of wheels and legs。” (來自here)
k-means的變種稱為k-modes,由Zhexue Huang在this paper中引入,適用於分類(類別)數據。請注意,這個解決方案對初始條件很敏感,例如,如here(PDF)所述。
Huang的論文(上麵鏈接)也有一個關於”k-prototypes”的部分,它適用於具有分類和數字特征的數據。它使用混合距離度量:分類特征的漢明距離和數字特征的歐幾裏德距離。
穀歌搜索“k-means混合分類數據”最近發表了很多關於k-means-like聚類的各種算法的論文,其中混合了類別和數值數據。 (我還沒看過,所以我不能評論他們的優缺點:)。)
實際上,你建議的(將分類屬性轉換為二進製值,然後將k-means轉換為數字值)是另一種嘗試之前的方法(早於k-modes)。 (參見Ralambondrainy,H.1995。概念版的k-means算法。模式識別快報,16:1147-1157。)但我認為k-modes方法是優選的,原因如上所述。
次佳解決方法
在我看來,有一些解決方案來處理聚簇中的分類數據。 比如R語言中就為類別數據提供特定距離度量。這個距離叫做Gower(http://www.rdocumentation.org/packages/StatMatch/versions/1.2.0/topics/gower.dist),效果很好。
第三種解決方法
這裏算是對上文的補充:
選擇k-modes聚類絕對是保證聚類穩定性的好方法。
-
聚類算法可以自由選擇任何距離度量/相似度得分。歐幾裏得是最受歡迎的。但是可以使用任何其他度量,其根據每個維度/屬性中的數據分布進行縮放,例如Mahalanobis度量。
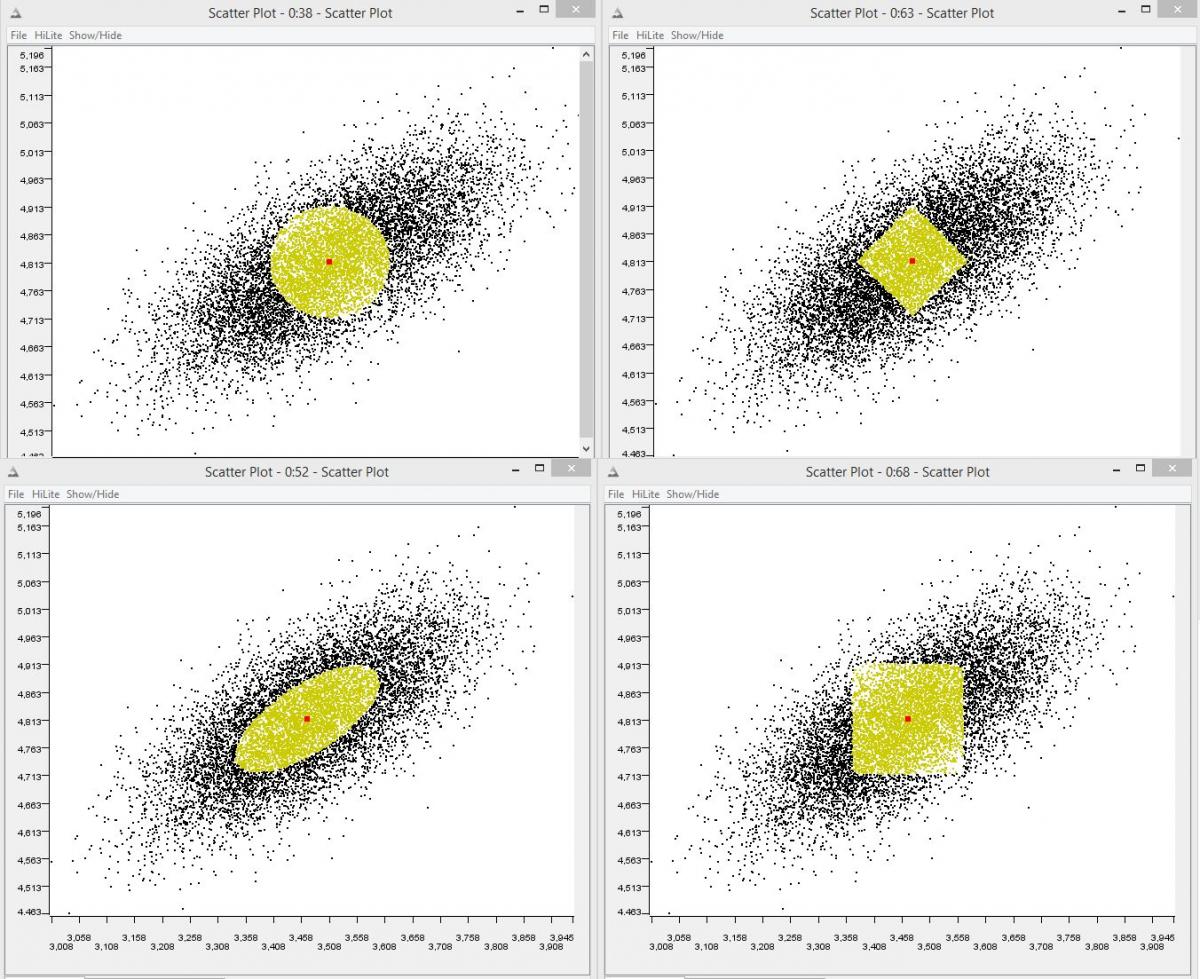
-
關於混合(數字和分類)聚類,可能有用的好文章是:INCONCO: Interpretable Clustering of Numerical and Categorical Objects
-
超越k-means:由於普通k-means已經被排除在這個問題的適當方法之外,不同的度量,如信息論:Kullback-Liebler divergence(KL散度)在嘗試將參數模型收斂到數據分布時效果很好。 (當然像GMM(高斯混合模型)這樣的參數化聚類技術比Kmeans慢,所以有一些缺點需要考慮)
-
模糊k-modes聚類聽起來也很吸引人,因為開發了模糊邏輯技術來處理分類數據之類的東西。有關更多信息,請參閱Fuzzy clustering of categorical data using fuzzy centroids。
另請查看:ROCK: A Robust Clustering Algorithm for Categorical Attributes
第四種方法
這個問題似乎與表示有關,而不是聚類方法。
類別數據是機器學習中大多數算法的問題。例如,假設您有一個名為”color”的分類變量,它可以采用紅色,藍色或黃色值。如果我們簡單地將這些數字分別編碼為1,2和3,我們的算法將認為red(1)實際上更接近藍色(2)而不是黃色(3)。我們需要使用一種表示,讓計算機理解這些東西實際上都是同樣不同的。
一種簡單的方法是使用所謂的one-hot表示,它正是您認為應該做的。我們不是像”color”這樣的變量可以采用三個值,而是將它分成三個變量。這些將是”color-red,” “color-blue,”和”color-yellow,”,它們隻能取值1或0。
這增加了空間的維度,但現在您可以使用任何您喜歡的聚類算法。在執行此過程後,有時對數據進行zscore或者白化是有意義的,但您的想法絕對合理。
