借助laplace_transform()方法,我們可以計算f(t)的拉普拉斯變換F(s)。
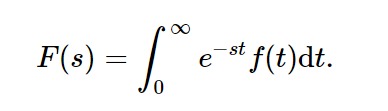
用法:laplace_transform(f, t, s)
返回:Return the laplace transformation and convergence condition.
範例1:
在這個例子中,我們可以通過使用laplace_transform()方法,我們能夠計算拉普拉斯變換並返回變換和收斂條件。
# import laplace_transform
from sympy.integrals import laplace_transform
from sympy.abc import t, s, a
# Using laplace_transform() method
gfg = laplace_transform(t**a, t, s)
print(gfg)輸出:
(s**(-a)*gamma(a + 1)/s, 0, a > -1)
範例2:
# import laplace_transform
from sympy.integrals import laplace_transform
from sympy.abc import t, s, a
# Using laplace_transform() method
gfg = laplace_transform(t**a, t, 5)
print(gfg)輸出:
(5**(-a)*gamma(a + 1)/5, 0, a > -1)
注:本文由純淨天空篩選整理自 sympy.integrals.transforms.laplace_transform() in python。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
