Python sympy.fibonacci()用法及代碼示例

借助於sympy.fibonacci()方法，我們可以在SymPy中找到斐波那契數和斐波那契多項式。

fibonacci(n) -
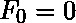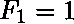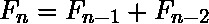The Fibonacci numbers are the integer sequence defined by the initial terms $F_0 = 0$ , $F_1 = 1$ and the two-term recurrence relation $F_n = F_{n-1} + F_{n-2}$ .

用法： fibonacci(n)

參數：
n - It denotes the number upto which Fibonacci number is to be calculated.

返回：Returns the n^th Fibonacci number.

範例1：

# import sympy  
from sympy import * 
  
n = 7
print("Value of n = {}".format(n)) 
   
# Use sympy.fibonacci() method  
nth_fibonacci = fibonacci(n)   
      
print("Value of nth fibonacci number:{}".format(nth_fibonacci))

輸出：

Value of n = 7
Value of nth fibonacci number:13

fibonacci(n, k) -

斐波那契多項式定義為，和 $F_n(k) = k*F_{n-1}(k) + F_{n-2}(k)$ 對於。對於所有正整數，。

用法： fibonacci(n, k)

參數：
n -它表示n^th斐波那契多項式。
k -它表示斐波那契多項式中的變量。

返回：返回k，F中的第n個斐波那契多項式_n(k)

範例2：

# import sympy  
from sympy import * 
  
n = 5
k = symbols('x') 
print("Value of n = {} and k = {}".format(n, k)) 
   
# Use sympy.fibonacci() method  
nth_fibonacci_poly = fibonacci(n, k)   
      
print("The nth fibonacci polynomial:{}".format(nth_fibonacci_poly))

輸出：

Value of n = 5 and k = x
The nth fibonacci polynomial:x**4 + 3*x**2 + 1

範例3：

# import sympy  
from sympy import * 
  
n = 6
k = 3
print("Value of n = {} and k = {}".format(n, k)) 
   
# Use sympy.fibonacci() method  
nth_fibonacci_poly = fibonacci(n, k)   
      
print("The nth fibonacci polynomial value:{}".format(nth_fibonacci_poly))

輸出：

Value of n = 6 and k = 3
The nth fibonacci polynomial value:360

相關用法

注：本文由純淨天空篩選整理自rupesh_rao大神的英文原創作品 Python | sympy.fibonacci() method。非經特殊聲明，原始代碼版權歸原作者所有，本譯文未經允許或授權，請勿轉載或複製。

fibonacci(n) - The Fibonacci numbers are the integer sequence defined by the initial terms , and the two-term recurrence relation . 用法： fibonacci(n) 參數： n - It denotes the number upto which Fibonacci number is to be calculated. 返回：Returns the nth Fibonacci number.

fibonacci(n, k) -