Python numpy random.mtrand.RandomState.standard_t用法及代碼示例

用法： RandomState.standard_t(df, size=None)

從df自由度的標準Student t分布中抽取樣本。

雙曲分布的一種特殊情況。隨著df變大，結果類似於標準正態分布(standard_normal)。

參數：	df：： float 或 array_like of floats 自由度必須> 0。 size：： int 或 tuple of ints, 可選參數輸出形狀。如果給定的形狀是`(m, n, k)`，然後`m * n * k`抽取樣品。如果尺寸是`None`(默認)，如果返回一個值`df`是標量。除此以外，`np.array(df).size`抽取樣品。
返回值：	out：： ndarray或標量從參數化的標準學生t分布中抽取樣本。

注意：

t分布的概率密度函數為

$P(x, df) = \frac{\Gamma(\frac{df+1}{2})}{\sqrt{\pi df} \Gamma(\frac{df}{2})}\Bigl( 1+\frac{x^2}{df} \Bigr)^{-(df+1)/2}$

t檢驗基於數據來自正態分布的假設。 t檢驗提供了一種方法來檢驗樣本均值(即根據數據計算出的均值)是否是真實均值的良好估計。

t-distribution的派生詞由William Gosset於1908年首次發布，當時他在都柏林的吉尼斯啤酒廠工作。由於專有問題，他不得不以化名出版，因此他使用了“學生”這個名字。

參考文獻：

[1]	彼得·達加德(Dalgaard)，“帶R的入門統計”，施普林格，2002年。

[2]	維基百科，“學生的t-distribution”https://en.wikipedia.org/wiki/Student’s_t-distribution

例子：

從達加德頁麵83[1]，假設11位女性的每日能量攝入量以千焦耳(kJ)為單位：

>>> intake = np.array([5260., 5470, 5640, 6180, 6390, 6515, 6805, 7515, \
...                    7515, 8230, 8770])

他們的能量攝入是否係統地偏離了7725 kJ的建議值？

我們有10個自由度，那麽樣本均值是否在建議值的95％以內？

>>> s = np.random.standard_t(10, size=100000)
>>> np.mean(intake)
6753.636363636364
>>> intake.std(ddof=1)
1142.1232221373727

計算t統計量，將ddof參數設置為無偏值，這樣標準偏差中的除數將為自由度N-1。

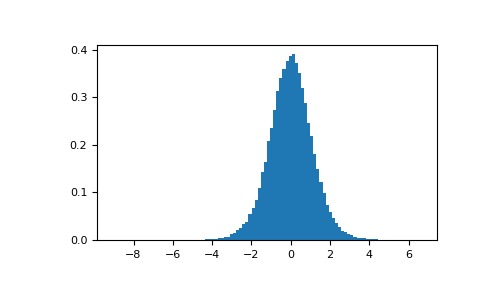
>>> t = (np.mean(intake)-7725)/(intake.std(ddof=1)/np.sqrt(len(intake)))
>>> import matplotlib.pyplot as plt
>>> h = plt.hist(s, bins=100, density=True)

對於one-sided t-test，t統計量在分布中顯示多遠？

>>> np.sum(s<t) / float(len(s))
0.0090699999999999999  #random

因此p-value約為0.009，這表示原假設的概率約為99％。

../../../_images/numpy-random-mtrand-RandomState-standard_t-1.png

注：本文由純淨天空篩選整理自 numpy.random.mtrand.RandomState.standard_t。非經特殊聲明，原始代碼版權歸原作者所有，本譯文未經允許或授權，請勿轉載或複製。