Python numpy random.mtrand.RandomState.dirichlet用法及代碼示例

用法： RandomState.dirichlet(alpha, size=None)

從Dirichlet分布中抽取樣本。

從Dirichlet分布中繪製尺寸為k的尺寸樣本。 Dirichlet-distributed隨機變量可以看作是Beta分布的多元概括。 Dirichlet分布是貝葉斯推斷中多項式分布的共軛先驗。

參數：	alpha：： array 分布參數(k維樣本為k維樣本)。 size：： int 或 tuple of ints, 可選參數輸出形狀。如果給定的形狀是`(m, n, k)`，然後`m * n * k`抽取樣品。默認值為無，在這種情況下，將返回單個值。
返回值：	samples：： ndarray，繪製的樣本，形狀(大小，alpha.ndim)。
異常：	ValueError：如果alpha中的任何值小於或等於零

注意：

Dirichlet分布是向量的分布滿足條件 x_i>0 和 $\sum_{i=1}^k x_i = 1$ 。

概率密度函數Dirichlet-distributed隨機向量與...成正比

$p(x) \propto \prod_{i=1}^{k}{x^{\alpha_i-1}_i},$

哪裏 $\alpha$ 是包含正濃度參數的向量。

該方法使用以下屬性進行計算：let是一個隨機向量，其分量遵循標準伽瑪分布，然後 $X = \frac{1}{\sum_{i=1}^k{Y_i}} Y$ 是Dirichlet-distributed

參考文獻：

[1]	David McKay，“信息論，推理和學習算法”，第23章，http://www.inference.org.uk/mackay/itila/

[2]	維基百科，“Dirichlet distribution”，https://en.wikipedia.org/wiki/Dirichlet_distribution

例子：

以Wikipedia中引用的示例為例，如果一個人想要將字符串(每個初始長度為1.0)切成不同長度的K個片段，則可以使用這種分布，其中每個片段平均具有指定的平均長度，但允許件的相對尺寸。

>>> s = np.random.dirichlet((10, 5, 3), 20).transpose()

>>> import matplotlib.pyplot as plt
>>> plt.barh(range(20), s[0])
>>> plt.barh(range(20), s[1], left=s[0], color='g')
>>> plt.barh(range(20), s[2], left=s[0]+s[1], color='r')
>>> plt.title("Lengths of Strings")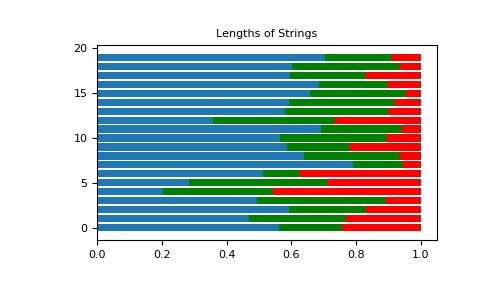

../../../_images/numpy-random-mtrand-RandomState-dirichlet-1.png

注：本文由純淨天空篩選整理自 numpy.random.mtrand.RandomState.dirichlet。非經特殊聲明，原始代碼版權歸原作者所有，本譯文未經允許或授權，請勿轉載或複製。