流圖本質上是2D圖的一種,主要由物理學家用來顯示流體流動和2D場梯度。在Matplotlib中創建流圖的基本函數是:
ax.streamplot(x_grid, y_grid, x_vec, y_vec, density=spacing)
這裏的x_grid和y_grid是x和y點的數組.x_vec和y_vec表示網格上每個點的流速度。屬性#density = spacing#指定將流線繪製在一起的緊密程度。
創建流圖-
首先,創建一個簡單的流圖,在10 x 10網格上包含流線。所有流線都是平行的並指向右側。以下代碼創建的流圖包含指向右側的水平平行線:
# Import libraries
import numpy as np
import matplotlib.pyplot as plt
# Creating dataset
x = np.arange(0, 10)
y = np.arange(0, 10)
# Creating grids
X, Y = np.meshgrid(x, y)
# x-component to the right
u = np.ones((10, 10))
# y-component zero
v = np.zeros((10, 10))
fig = plt.figure(figsize = (12, 7))
# Plotting stream plot
plt.streamplot(X, Y, u, v, density = 0.5)
# show plot
plt.show()輸出:

在這裏,x和y是等距網格上的一維數組,u和v是x和y速度的2D數組,其中行數應與y的長度匹配,而列數應與x的密度匹配,一個控製流線的緊密度的float值。
定製流圖-
借助streamplot()函數,我們可以基於定義的2D矢量場創建和定製顯示場線的繪圖。許多屬性在streamplot()修改圖的函數。
# Import libraries
import numpy as np
import matplotlib.pyplot as plt
# Creating data set
w = 3
Y, X = np.mgrid[-w:w:100j, -w:w:100j]
U = -1 - X**2 + Y
V = 1 + X - Y**2
speed = np.sqrt(U**2 + V**2)
# Creating plot
fig = plt.figure(figsize = (12, 7))
plt.streamplot(X, Y, U, V, density = 1)
# show plot
plt.show()輸出:
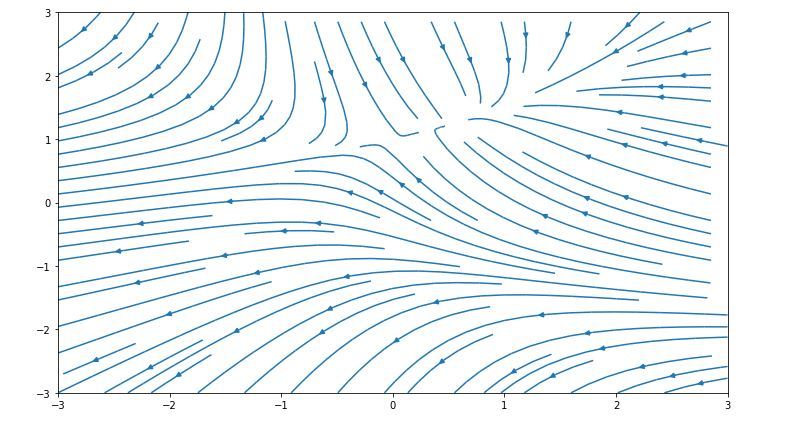
下麵列出了上麵圖形的一些自定義項:
改變流線的密度-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
# Creating dataset
w = 3
Y, X = np.mgrid[-w:w:100j, -w:w:100j]
U = -1 - X**2 + Y
V = 1 + X - Y**2
speed = np.sqrt(U**2 + V**2)
fig = plt.figure(figsize =(24, 20))
gs = gridspec.GridSpec(nrows = 3, ncols = 2,
height_ratios =[1, 1, 2])
# Varying the density along a
# streamline
ax = fig.add_subplot(gs[0, 0])
ax.streamplot(X, Y, U, V,
density =[0.4, 0.8])
ax.set_title('Varying the density along a streamline')
# show plot
plt.tight_layout()
plt.show()輸出:
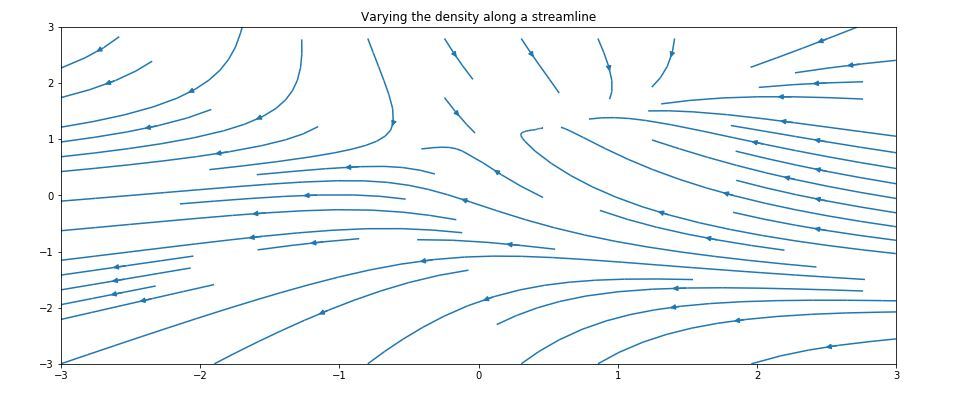
沿流線改變顏色-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
# Creating dataset
w = 3
Y, X = np.mgrid[-w:w:100j, -w:w:100j]
U = -1 - X**2 + Y
V = 1 + X - Y**2
speed = np.sqrt(U**2 + V**2)
fig = plt.figure(figsize =(24, 20))
gs = gridspec.GridSpec(nrows = 3, ncols = 2,
height_ratios =[1, 1, 2])
# Varying color along a streamline
ax = fig.add_subplot(gs[0, 1])
strm = ax.streamplot(X, Y, U, V, color = U,
linewidth = 2, cmap ='autumn')
fig.colorbar(strm.lines)
ax.set_title('Varying the color along a streamline.')
# show plot
plt.tight_layout()
plt.show() 輸出:
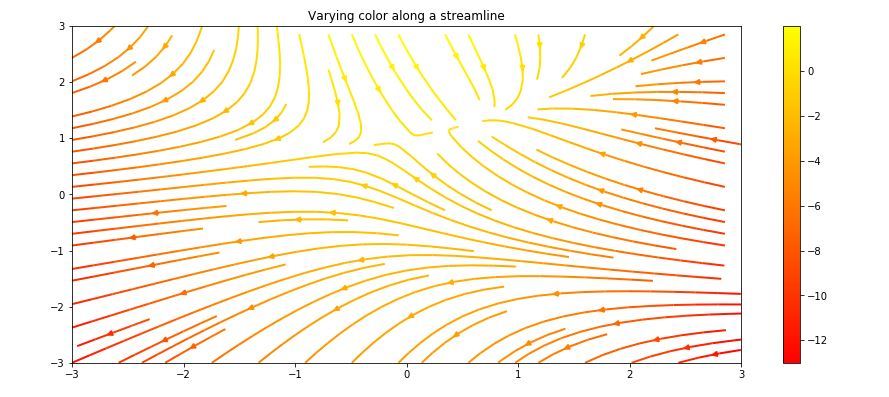
沿流線改變線寬-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
# Creating dataset
w = 3
Y, X = np.mgrid[-w:w:100j, -w:w:100j]
U = -1 - X**2 + Y
V = 1 + X - Y**2
speed = np.sqrt(U**2 + V**2)
fig = plt.figure(figsize =(24, 20))
gs = gridspec.GridSpec(nrows = 3, ncols = 2,
height_ratios =[1, 1, 2])
# Varying line width along a streamline
ax = fig.add_subplot(gs[1, 0])
lw = 5 * speed / speed.max()
ax.streamplot(X, Y, U, V, density = 0.6,
color ='k', linewidth = lw)
ax.set_title('Varying line width along a streamline')
# show plot
plt.tight_layout()
plt.show()輸出:
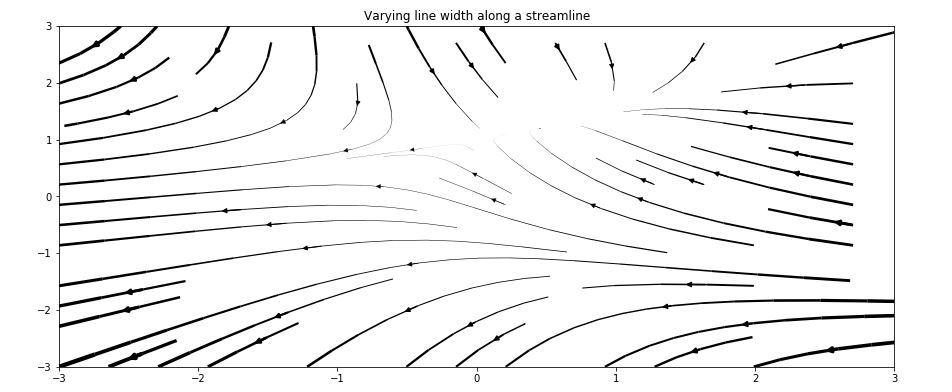
控製流線的起點-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
# Creating dataset
w = 3
Y, X = np.mgrid[-w:w:100j, -w:w:100j]
U = -1 - X**2 + Y
V = 1 + X - Y**2
speed = np.sqrt(U**2 + V**2)
fig = plt.figure(figsize =(24, 20))
gs = gridspec.GridSpec(nrows = 3, ncols = 2,
height_ratios =[1, 1, 2])
# Controlling the starting points
# of the streamlines
seek_points = np.array([[-2, -1, 0, 1, 2, -1],
[-2, -1, 0, 1, 2, 2]])
ax = fig.add_subplot(gs[1, 1])
strm = ax.streamplot(X, Y, U, V, color = U,
linewidth = 2,
cmap ='autumn',
start_points = seek_points.T)
fig.colorbar(strm.lines)
ax.set_title('Controlling the starting\
points of the streamlines')
# Displaying the starting points
# with blue symbols.
ax.plot(seek_points[0], seek_points[1], 'bo')
ax.set(xlim =(-w, w), ylim =(-w, w))
# show plot
plt.tight_layout()
plt.show()輸出:
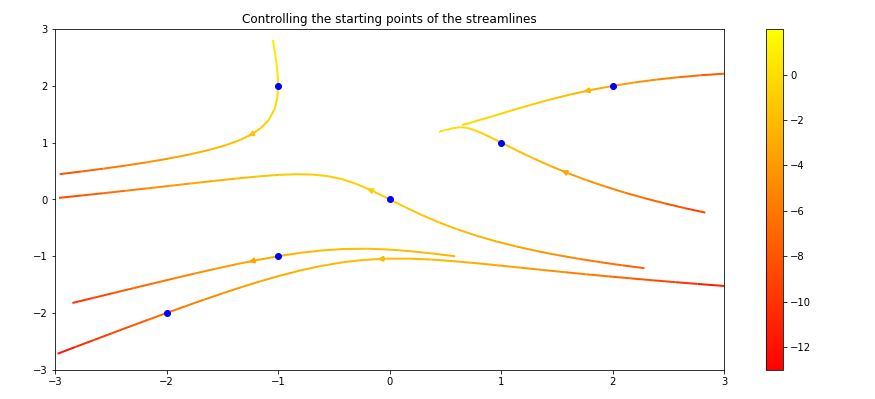
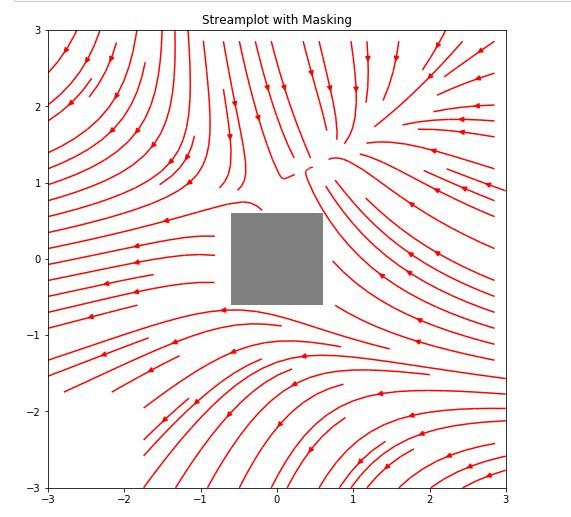
簡化跳過遮罩區域和NaN值的流程-
# Import libraries
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
# Creating dataset
w = 3
Y, X = np.mgrid[-w:w:100j, -w:w:100j]
U = -1 - X**2 + Y
V = 1 + X - Y**2
speed = np.sqrt(U**2 + V**2)
fig = plt.figure(figsize =(20, 16))
gs = gridspec.GridSpec(nrows = 3, ncols = 2, height_ratios =[1, 1, 2])
# Create a mask
mask = np.zeros(U.shape, dtype = bool)
mask[40:60, 40:60] = True
U[:20,:20] = np.nan
U = np.ma.array(U, mask = mask)
ax = fig.add_subplot(gs[2:,:])
ax.streamplot(X, Y, U, V, color ='r')
ax.set_title('Streamplot with Masking')
ax.imshow(~mask, extent =(-w, w, -w, w), alpha = 0.5,
interpolation ='nearest', cmap ='gray', aspect ='auto')
ax.set_aspect('equal')
# show plot
plt.tight_layout()
plt.show()輸出:
例:
流圖顯示兩點電荷引起的電場,表麵上任何一點的電場取決於兩個電荷之間的位置和距離:
import sys
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
# Function to determin electric field
def E(q, r0, x, y):
den = np.hypot(x-r0[0], y-r0[1])**3
return q * (x - r0[0]) / den, q * (y - r0[1]) / den
# Grid of x, y points
nx, ny = 64, 64
x = np.linspace(-2, 2, nx)
y = np.linspace(-2, 2, ny)
X, Y = np.meshgrid(x, y)
# Create a multipole with nq charges of
# alternating sign, equally spaced
# on the unit circle.
# Increase the power with increase in charge
nq = 2**1
charges = []
for i in range(nq):
q = i % 2 * 2 - 1
charges.append((q, (np.cos(2 * np.pi * i / nq),
np.sin(2 * np.pi * i / nq))))
# Electric field vector, E =(Ex, Ey)
# as separate components
Ex, Ey = np.zeros((ny, nx)), np.zeros((ny, nx))
for charge in charges:
ex, ey = E(*charge, x = X, y = Y)
Ex += ex
Ey += ey
fig = plt.figure(figsize =(18, 8))
ax = fig.add_subplot(111)
# Plotting the streamlines with
# proper color and arrow
color = 2 * np.log(np.hypot(Ex, Ey))
ax.streamplot(x, y, Ex, Ey, color = color,
linewidth = 1, cmap = plt.cm.inferno,
density = 2, arrowstyle ='->',
arrowsize = 1.5)
# Add filled circles for the charges
# themselves
charge_colors = {True:'#AA0000',
False:'#0000AA'}
for q, pos in charges:
ax.add_artist(Circle(pos, 0.05,
color = charge_colors[q>0]))
ax.set_xlabel('X-axis')
ax.set_ylabel('X-axis')
ax.set_xlim(-2, 2)
ax.set_ylim(-2, 2)
ax.set_aspect('equal')
plt.show()輸出:
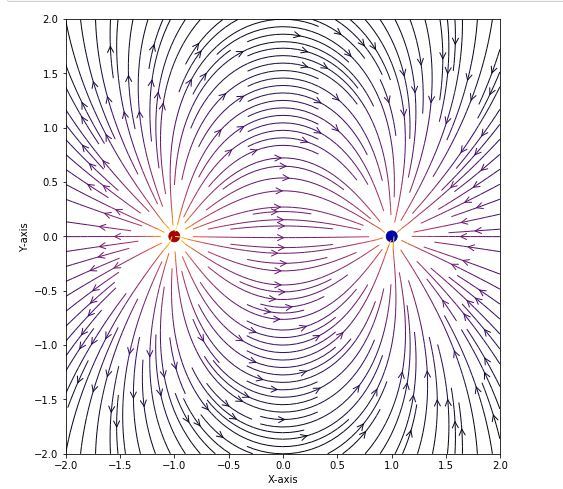
相關用法
注:本文由純淨天空篩選整理自jeeteshgavande30大神的英文原創作品 Matplotlib.pyplot.streamplot() in Python。非經特殊聲明,原始代碼版權歸原作者所有,本譯文未經允許或授權,請勿轉載或複製。
