
動態規劃(DP)問題是常見的麵試問題,雖然這類問題在是否能有效評估某人在工程上的表現能力存疑,但是許多當紅炸子雞科技公司還是熱衷於在麵試中考察DP。如果候選人沒有掌握解DP問題的套路,很可能在麵試中遭遇滑鐵盧!
解決動態規劃(DP)問題的7個步驟
通過閱讀本文,你可以判斷問題是否為“DP 問題”並找出解決該方法。具體來說,需要執行以下7個步驟:
- 如何識別DP問題
- 識別問題變量
- 清楚表達遞歸關係
- 確定初始情況
- 確定是要迭代實現還是遞歸實現
- 添加備忘錄
- 確定時間複雜度
DP問題示例
這裏介紹一個示例問題。在每個步驟的詳細介紹部分,我都會提到這個問題,但是您也可以獨立於問題閱讀這些部分。
問題陳述:

瘋狂的彈跳球遊戲:在此問題中,我們處於瘋狂的跳躍球上,試圖停下來,同時要在行進過程避免沿途出現的尖峰。
規則如下:
1)您有一條平坦的跑道,但上麵有一束尖刺。跑道由布爾數組表示,該布爾數組指示特定(離散)點是否有尖峰。清除了尖峰的則為True,沒有清除的為False。
數組表示示例:

2)您獲得的起始速度為S。S是任意給定點的非負整數,它表示您將在下一次跳躍時前進多少。
3)每次降落在地麵上時,在下一次跳躍之前,您最多可以將速度調整1個單位。
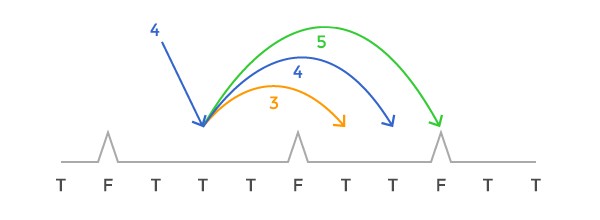
4)您想要安全地在跑道上的任何地方停下來(不必在道路(數組)的盡頭)。當速度變為0時,您會停下來。但是,如果您在任何時候落在尖峰上,瘋狂的彈跳球都會爆裂,比賽結束,遊戲失敗!
函數的輸出應為布爾值,指示我們是否可以在跑道上的某個地方安全地停止。
步驟1:如何識別動態編程問題
首先,我們要弄清楚DP本質上隻是一種優化技術。 DP是一種解決問題的方法,它可以將問題分解為更簡單的子問題的集合,僅解決一次這些子問題,然後存儲其解決方案。下一次出現相同的子問題時,您無需重新計算其解決方案,隻需查找先前計算出的解決方案即可。這節省了計算時間,但以(預期可接受的)適度的存儲空間開銷為代價。
認識到可以使用DP解決問題是解決問題的第一步,也是最困難的一步。您想問自己的問題是,您的問題解決方案是否可以表示為類似的較小問題的解決方案的函數。
在我們的示例問題中,給定跑道上的某個點,速度和前方的跑道情況,我們可以確定下一個可能跳下的位置。此外,似乎我們是否可以以當前速度從當前點停止,僅取決於我們是否可以從選擇前往下一點的點停止。
這是一件很了不起的事情,因為通過向前發展,我們縮短了跑道,並使我們的問題更小。我們應該能夠一直重複這一過程,直到我們可以停下來為止。
認識到動態編程問題通常是解決它的最困難的步驟。問題解決方案可以表達為類似較小問題的解決方案的函數嗎?
步驟2:找出問題變數
現在我們已經確定在子問題之間存在一些遞歸結構。接下來,我們需要根據功能參數來表達問題,並查看其中哪些參數正在更改。
通常,在訪談中,您將擁有一個或兩個變化的參數,但從技術上講,它可以是任意數量。 one-changing-parameter問題的經典示例是“確定n-th斐波那契數”。 two-changing-parameters問題的此類示例是“計算字符串之間的編輯距離”。如果您不熟悉這些問題,請不必擔心。
確定更改參數數量的一種方法是列出幾個子問題的示例並比較參數。計算不斷變化的參數數量對於確定我們必須解決的子問題數量很有價值。它本身也很重要,可以幫助我們加強對步驟1中的遞歸關係的理解。
在我們的示例中,每個子問題可能更改的兩個參數是:
- 陣列位置(P)
- 速度(S)
可以說前麵的跑道也在發生變化,但是考慮到整個不變的跑道和位置(P)已經攜帶了該信息,那將是多餘的。
現在,有了這兩個變化的參數和其他靜態參數,我們對sub-problems有了完整的描述。
確定變化的參數並確定子問題的數量。
步驟3:清楚表達遞歸關係
這是許多人為了編碼而急需完成的重要步驟。盡可能清晰地表達遞歸關係將增強您對問題的理解,並使其他所有事情都變得更加容易。
一旦確定了遞歸關係並根據參數指定了問題,這將是自然而然的步驟。問題如何相互聯係?換句話說,假設您已經計算了子問題。您將如何計算主要問題?
這是我們在示例問題中的思考方式:
因為在跳到下一個位置之前您最多可以將速度調整為1,所以隻有3種可能的速度,因此有3個點可以成為下一個位置。
更正式地說,如果我們的速度是S,即位置P,則可以從(S,P)轉到:
- (S,P + S); #如果我們不改變速度
- (S_1,P + S_1); #如果我們將速度更改為-1
- (S + 1,P + S + 1); #如果我們將速度更改+1
如果我們可以找到一種方法來停止上述任何子問題,那麽我們也可以從(S,P)處停止。這是因為我們可以從(S,P)過渡到以上三個選項中的任何一個。
通常,這是對問題的很好理解(簡單的英語解釋),但是有時您可能還希望用數學方式表達這種關係。讓我們調用一個我們要計算canStop的函數。然後:
canStop(S,P)= canStop(S,P + S)|| canStop(S _1,P + S _1)|| canStop(S + 1,P + S + 1)
oo,看來我們有重複關係!
遞歸關係:假設您已經計算了子問題,那麽您將如何計算主要問題?
步驟4:確定基本情況
基本案例是一個子問題,它不依賴於任何其他子問題。為了找到此類子問題,您通常需要嘗試一些示例,看看您的問題如何簡化為較小的子問題,並確定在什麽時候無法進一步簡化。
無法進一步簡化問題的原因是,參數之一將變為在給定的情況下不可能的值約束問題。
在示例問題中,我們有兩個變化的參數S和P。讓我們考慮一下S和P的哪些可能的值不合法:
- P應該在給定跑道的範圍內
- P不能表示跑道[P]為假,因為那將意味著我們正處於高峰
- S不能為負,並且S == 0表示我們已經完成
有時,將我們對參數所做的斷言轉換為可編程基本情況可能會有些挑戰。這是因為,如果要使代碼看起來簡潔而不檢查不必要的條件,則除了列出斷言之外,還需要考慮這些條件中的哪一個是可能的。
在我們的示例中:
- P =跑道長度似乎是正確的事情。另一種選擇是考慮P ==跑道盡頭基本情況。但是,問題有可能分解成超出跑道末端的子問題,因此我們確實需要檢查不平等性。
- 這似乎很明顯。我們可以簡單地檢查如果跑道[P]為假。
- 與#1類似,我們可以簡單地檢查SS == 0是S參數的足夠基本情況。
第5步:確定您要迭代還是遞歸實現
到目前為止,我們談論步驟的方式可能會讓您認為我們應該遞歸地解決問題。但是,到目前為止,我們所討論的一切都與您決定遞歸還是迭代實施該問題完全無關。在這兩種方法中,您都必須確定遞歸關係和基本案例。
要決定是迭代還是遞歸,您需要仔細考慮一下trade-offs。
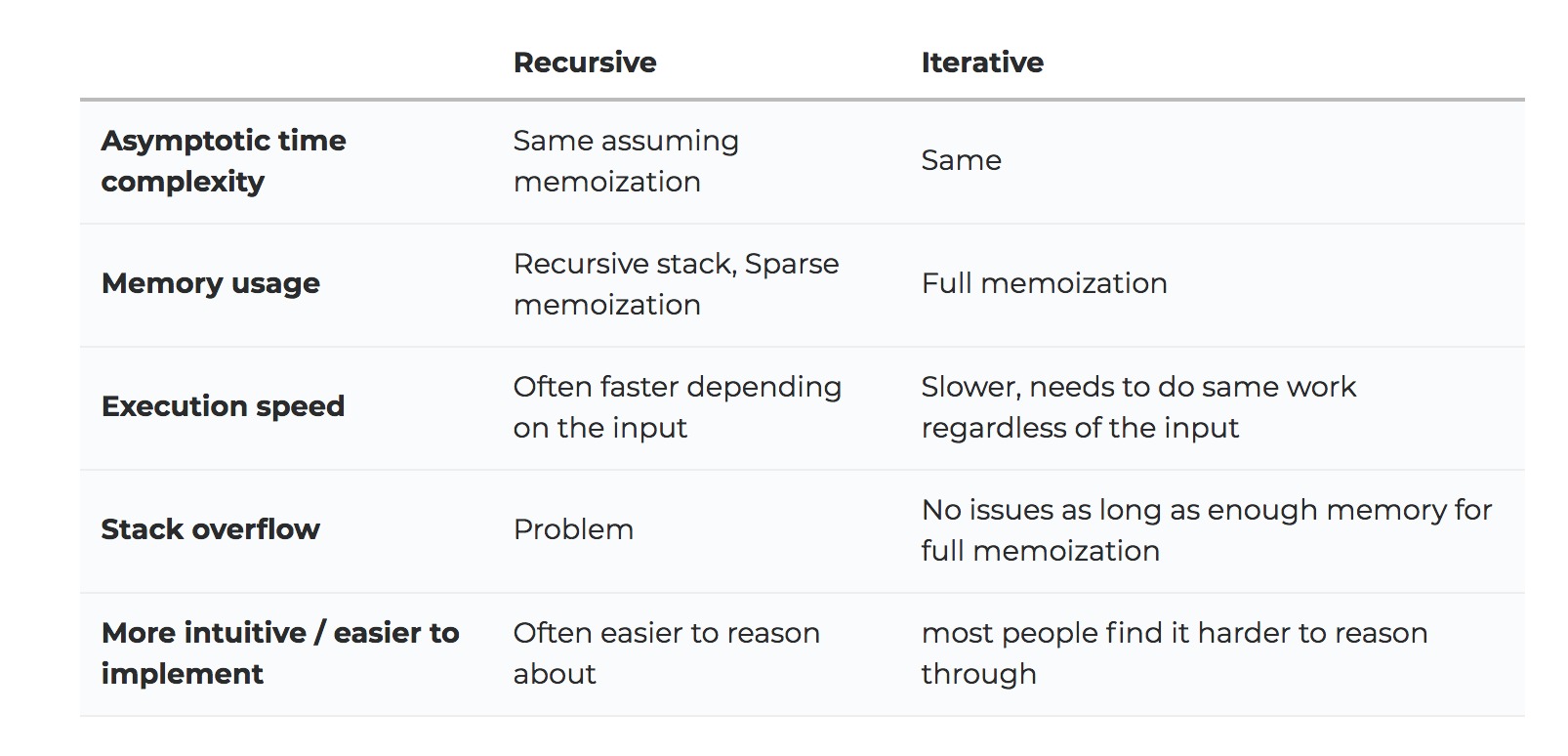
堆棧溢出問題通常是破壞交易的因素以及您不希望在(後端)生產係統中進行遞歸的原因。但是,出於訪談的目的,隻要您提到trade-offs,通常都可以使用任何一種實現。您應該對兩者都感到滿意。
在我們的特定問題中,我實現了兩個版本。這是為此的python代碼:
遞歸解決方案:(可以找到原始代碼段這裏)
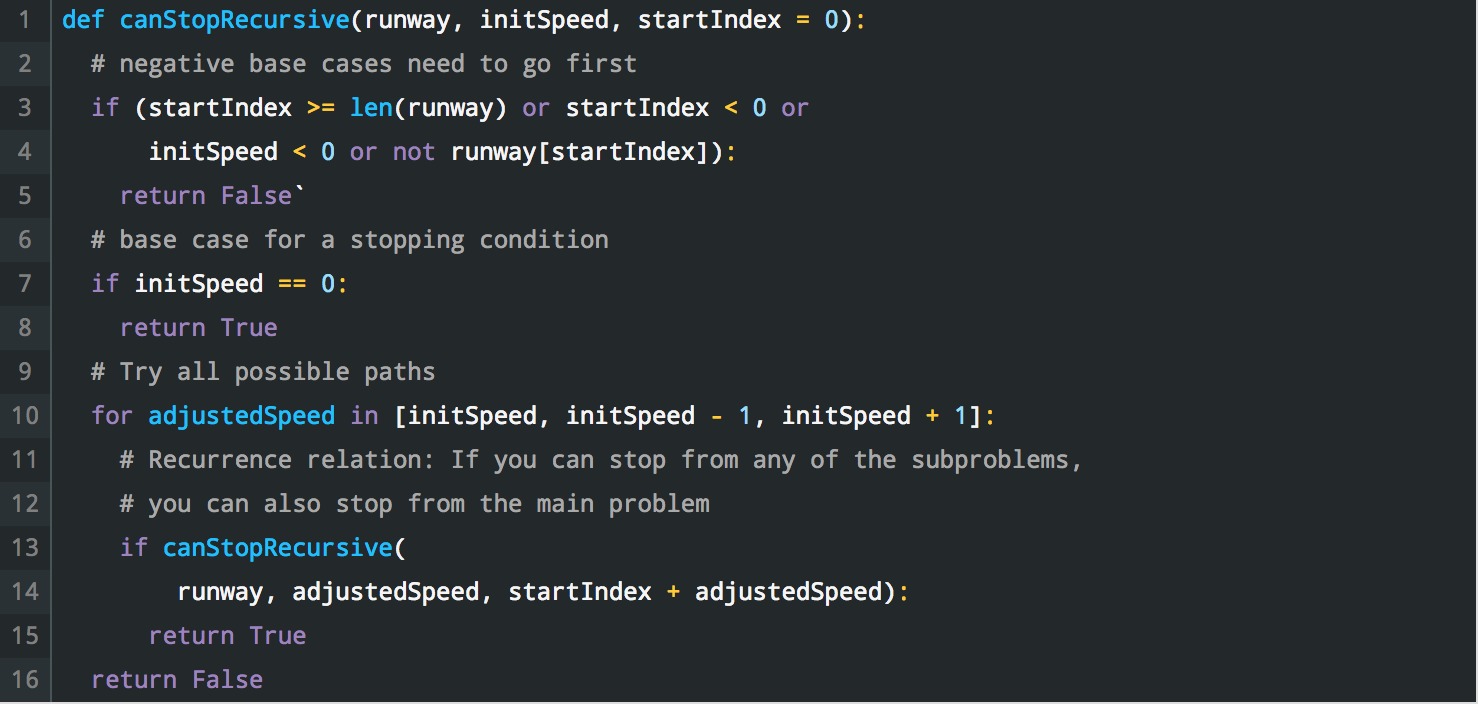
迭代解決方案:(可以找到原始代碼段這裏)
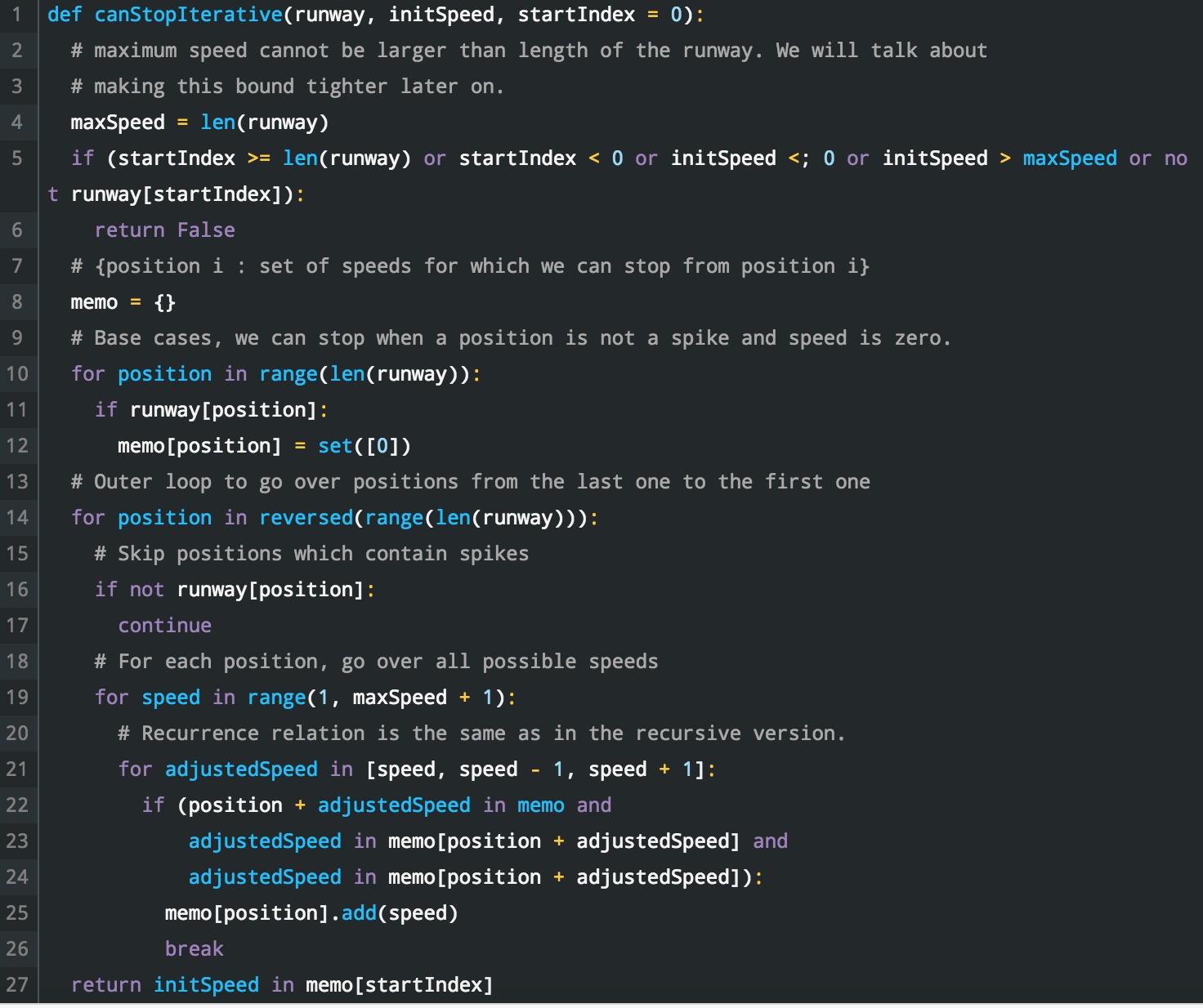
步驟6:添加備忘錄
memory 化是與DP緊密相關的技術。它用於存儲昂貴的函數調用的結果,並在再次出現相同的輸入時返回緩存的結果。
我們為什麽要在遞歸中添加備忘錄?我們遇到相同的子問題,這些子問題在沒有備忘的情況下被重複計算。這些重複經常導致指數時間複雜性。
在遞歸解決方案中,添加備忘錄應該很簡單。讓我們看看為什麽。請記住, memory 隻是函數結果的緩存。有時您可能會偏離此定義以擠出一些次要的優化,但是將備忘錄作為函數結果緩存是實現它的最直觀的方法。
這意味著您應該:
- 每次都將函數結果存儲到內存中返回 聲明
- 在開始執行任何其他計算之前,先在內存中查找函數結果
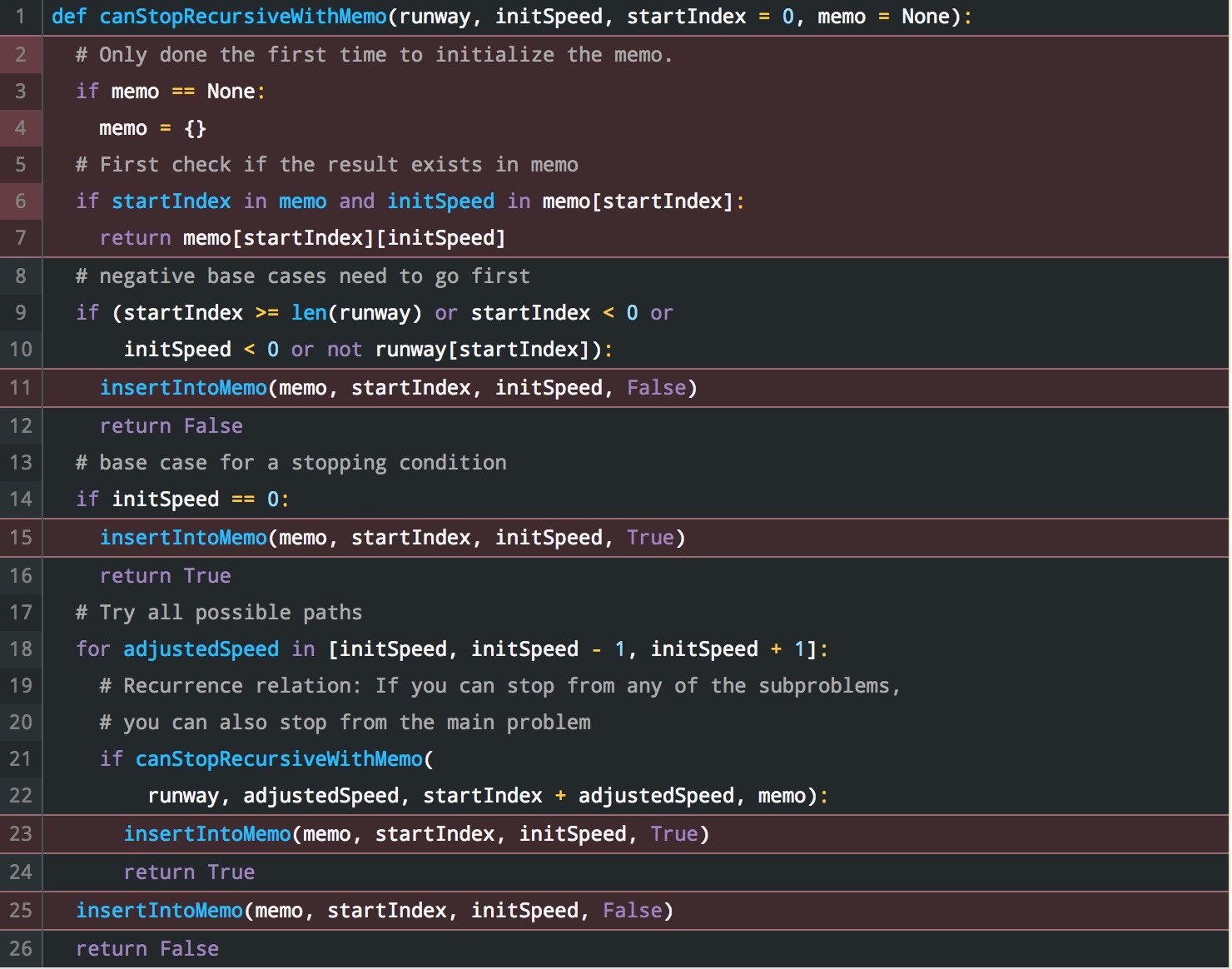
這是上麵添加了備注的代碼(突出顯示了幾行):(可以找到原始代碼段這裏)
為了說明 memory 和不同方法的有效性,讓我們進行一些快速測試。我將對到目前為止已經看到的所有三種方法進行壓力測試。設置如下:
- 我創建了一個長度為1000的跑道,在隨機位置出現尖峰(我選擇在任何給定位置使尖峰的概率為20%)
- initSpeed = 30
- 我運行了所有功能10次,並測量了平均執行時間
結果如下(以秒為單位):

您可以看到,純遞歸方法所花的時間比迭代方法多500倍,比帶 memory 的遞歸方法多1300倍。請注意,這種差異會隨著跑道的長度而迅速增加。我鼓勵您嘗試自己運行它。
步驟7:確定時間複雜度
有一些簡單的規則可以使動態編程問題的計算時間複雜度大大降低。您需要執行以下兩個步驟:
- 計算狀態數-這取決於問題中更改參數的數量
- 想想每個州完成的工作。換句話說,如果除一個狀態外的所有其他內容都已計算,那麽您需要做多少工作才能計算出最後一個狀態?
在我們的示例問題中,狀態數為| P | * | S |,哪裏
- P是所有位置的集合(| P |表示P中的元素數)
- S是所有速度的集合
在此問題中,每個狀態的工作量為O(1),因為給定所有其他狀態,我們隻需查看3個子問題即可確定結果狀態。
正如我們在前麵的代碼中指出的,| S |受跑道長度(| P |)的限製,因此我們可以說狀態數為| P |²,並且由於每個狀態所做的工作為O(1),所以總時間複雜度為O(| P |²)。
但是,似乎| S |可以進一步限製,因為如果確實是| P |,很顯然將無法停止,因為您必須在第一步中跳過整個跑道的長度。
因此,讓我們看看如何對| S |進行更嚴格的限製。我們將最大速度稱為S。假設我們從位置0開始。如果我們試圖盡快停止並且忽略潛在的峰值,我們能停止多久?

在第一輪迭代中,我們必須至少將速度調整到零(S-1),方法是將零速調整為-1。從那裏我們至少要前進(S-2)步,依此類推。
對於跑道長度L,必須滿足以下條件:
=> (S-1)+(S-2)+(S-3)+…。+ 1
=> S *(S-1)/2
=> S²— S — 2公升
如果找到上述函數的根,它們將是:
r1 = 1/2 + sqrt(1/4 + 2L)和r2 = 1/2-sqrt(1/4 + 2L)
我們可以將不等式寫成:
(S — r1)*(S — r2)
考慮到S_r2>對於任何S> 0 0且L> 0,我們需要以下內容:
S — 1/2 —平方尺(1/4 + 2L)
=>小號
那是我們在長度為L的跑道上可能擁有的最大速度。如果速度高於該速度,則無論尖峰的位置如何,理論上我們都無法停止。
這意味著總時間複雜度僅取決於跑道L的長度,形式如下:
O(L * sqrt(L))比O(L²)好
O(L * sqrt(L))是時間複雜度的上限
太棒了,您成功了! 🙂
我們經過的7個步驟應為您提供一個係統解決所有動態編程問題的框架。我強烈建議您針對更多問題練習這種方法,以完善您的方法。
這是您可以采取的一些後續步驟
- 通過嘗試找到到停止點的路徑來擴展樣本問題。我們解決了一個問題,告訴您是否可以停止,但是如果您還想知道為了最終在跑道上停止所要采取的步驟,該怎麽辦?您將如何修改現有的實現方式?
- 如果要鞏固對 memory 的理解,並了解它隻是一個函數結果緩存,則應閱讀有關Python的裝飾器或其他語言的類似概念的信息。考慮一下它們將如何允許您總體上實現要記住的任何功能的記住。
- 按照我們經過的步驟處理更多DP問題。您總是可以在網上找到一大堆(例如LeetCode要麽極客)。在練習時,請記住一件事:學習想法,不要學習問題。創意的數量大大減少,征服的空間更輕鬆,也可以為您提供更好的服務。
當您覺得自己已經征服了這些想法時,請查看Refdash在這裏,您將接受高級工程師的麵試,並獲得有關您的編碼,算法和係統設計的詳細反饋。
